問題
(1) \( \sqrt[3]{2} \)が無理数であることを証明せよ。
(2) \( P(x) \)は有理数を係数とする\( x \)の多項式で, \( P(\sqrt[3]{2}) = 0 \)を満たしているとする。このとき\( P(x) \)は\( x^3 – 2 \)で割り切れることを証明せよ。
発想
(1)は, \( \sqrt{2} \)が無理数であることの証明を参考にする。
(2)は, 多項式の割り算なので, \( P(x) = (x^3 – 2)Q(x) + ax^2 + bx + c \)とおき, \( a = b = c = 0 \)を示す, という方針を立てるまでは一本道。
下書き
(1)
\( \sqrt{2} \)が無理数であることの証明を確認しておく。
有理数だと仮定すると, \( \sqrt{2} = \frac{q}{p} \)(\( p, q \)は互いに素な自然数1)とおける。
よって, \( 2p^2 = q^2 \)…①となるが, 左辺が\( 2 \)の倍数なので, \( q^2 \)も\( 2 \)の倍数である。
したがって, \( q \)も\( 2 \)の倍数であるから, 改めて\( q = 2q’ \)(\( q’ \)は自然数)とおくと, ①は, \( p^2 = 2q’^2 \)となる。同様の議論で, \( p \)も\( 2 \)の倍数となるが, これは\( p, q \)が互いに素ということに矛盾する。
これと同様にやれば(1)は終了。
(2)
\( P(x) \)を\( x^3 – 2 \)で割ったときの商を\( Q(x) \), 余りを\( ax^2 + bx + c \)とすると, \( P(x) = (x^3 – 2)Q(x) + ax^2 + bx + c \)と置ける。
すると, \( P(\sqrt[3]{2}) = 0 \)より, \( a(\sqrt[3]{2})^2 + b\sqrt[3]{2} + c = 0 \)となる。割り切れることの証明なので, \( a = b = c = 0 \)を示すことが目標。
式をよく見ると, \( (\sqrt[3]{2})^2 \)も無理数だろうから, 「\( a,b,c \)が有理数で, \( X,Y \)が無理数のとき, \( a + bX + cY = 0 \)ならば\( a = b = c = 0 \)」…②と同じ構造をしている。
これは, もしかしたら当たり前だと思うかもしれない。
しかし, 証明が過去にも出題されており, そもそも無理数\( X,Y \)の値によっては成り立たない。
参照 1999年度 理系第5問
ここでポイントは, 「\( a,b \)が有理数で, \( X \)が無理数のとき, \( a + bX = 0 \)ならば\( a = b = 0 \)」…③はすぐに示せることである。
背理法的に, もし\( a \neq 0 \)であれば\( X = -\frac{a}{b} \)と変形できるが, 左辺は無理数, 右辺は有理数となり矛盾。よって, \( a = 0 \)で, したがって\( b \)も\( 0 \)だから③は成り立つ。
②と③の違いは, 無理数が一つか二つかの違いである。よって, 無理数を一つにまとめてしまえば, 証明が簡単にできる。
ただし今回は\( 3 \)乗根なので, 移行して\( 3 \)乗するだけでは根号(無理数)が二つ残ってしまう。慎重に考えて式変形を行う。
まず, \( a(\sqrt[3]{2})^2 + b\sqrt[3]{2} + c = 0 \)…④の式がある。
この式だけでは, 根号を一つにできないので, 例えば\( \sqrt[3]{2} \)を両辺に掛けると, \( (\sqrt[3]{2})^3 = 2 \)が使えて, \( 2a + b(\sqrt[3]{2})^2 + c\sqrt[3]{2} = 0 \)…⑤となる。
④⑤で, \( \sqrt[3]{2} \)と\( (\sqrt[3]{2})^2 \)の連立方程式みたいになったので, 消去できるはずである。
どちらでもよいが, ややこしそうな\( (\sqrt[3]{2})^2 \)の方を消去してみると, \( (\color{red}{ac – b^2})\sqrt[3]{2} = \color{red}{bc – 2a^2} \)となる2。
これで無理数が一つになったので, 上と同様に, \( \color{red}{ac – b^2} = \color{red}{bc – 2a^2} = 0 \)が言える。
あとはここから\( a = b = c = 0 \)を言えばよいだけ。
すぐに示すのは難しいが, 手を動かしていると, \( ac = b^2 \)と\( bc = 2a^2 \)を返々割ると綺麗になることに気づく。\( c \)は消えて, \( a,b \)も, \( \frac{b}{a} \)だけで表せる, いわゆる斉次式の形になる。よって, この式変形が正しそう。
辺々割るには, 分母\( \neq 0 \)が必要で, 割った式を整理すると, \( \sqrt[3]{2} = \frac{b}{a} \)となる。
しかしこれは左辺が無理数, 右辺が有理数となるので, 矛盾が生じ, 辺々割ったところ, つまり分母\( \neq 0 \)としたところが間違っていたことが分かる。
このようにして, \( a = b = c = 0 \)が言える。
解答例
(1)
\( \sqrt[3]{2} \)が有理数だと仮定すると, 互いに素な自然数\( p, q \)を用いて, \( \sqrt[3]{2} = \frac{q}{p} \)とおける。
\( 3 \)乗して分母を払うと, \( 2p^3 = q^3 \)…①となる。
左辺は\( 2 \)の倍数なので, 右辺の\( q^3 \)も\( 2 \)の倍数である。したがって, \( q \)も\( 2 \)の倍数である。
自然数\( q’ \)を用いて\( q = 2q’ \)と改めておくと, ①は\( p^3 = 4q’^3 \)となる。
右辺は\( 2 \)の倍数なので, 左辺の\( p^3 \)も\( 2 \)の倍数である。したがって, \( p \)も\( 2 \)の倍数である。
しかしこれは, \( p, q \)が互いに素であるということに矛盾する。
よって, \( \sqrt[3]{2} \)は無理数である。
(2)
\( P(x) \)を\( x^3 – 2 \)で割ったときの商を\( Q(x) \), 余りを\( ax^2 + bx + c \)とすると, \( P(x) = (x^3 – 2)Q(x) + ax^2 + bx + c \)と置ける。
ここで, \( P(x) \)は有理数係数より, \( a,b,c \)は全て有理数である。
すると, \( P(\sqrt[3]{2}) = 0 \)より, \( a(\sqrt[3]{2})^2 + b\sqrt[3]{2} + c = 0 \)…②となる。
②の両辺に\( \sqrt[3]{2} \)を掛けて, \( 2a + b(\sqrt[3]{2})^2 + c\sqrt[3]{2} = 0 \)…③
②③より\( (\sqrt[3]{2})^2 \)を消去して整理すると, \( (ac – b^2)\sqrt[3]{2} = bc – 2a^2 \)…④
\( ac – b^2 \neq 0 \)とすると, \( (ac – b^2)\sqrt[3]{2} = bc – 2a^2 \)④は\( \sqrt[3]{2} = \frac{bc – 2a^2}{ac – b^2} \)と変形できるが, これは, (1)より左辺が無理数, \( a,b,c \)は全て有理数より右辺が有理数となり, 矛盾。
よって, \( ac – b^2 = 0 \)…⑤であり, \( (ac – b^2)\sqrt[3]{2} = bc – 2a^2 \)④に代入すると, \( bc – 2a^2 = 0 \)…⑥
ここで, もし\( b^2 \neq 0 \)かつ\( ac \neq 0 \)ならば, ⑤:\( ac = b^2 \)と⑥:\( bc = 2a^2 \)を辺々割り, \( \frac{2a^2}{b^2} = \frac{b}{a} \)となる。整理すると, \( \sqrt[3]{2} = \frac{b}{a} \)となるが, (1)より左辺が無理数, 右辺が有理数となり, 矛盾。
よって, \( b^2 = 0 \)または\( ac = 0 \)である。
(i) \( b^2 = 0 \)すなわち\( b = 0 \)のとき, \( bc – 2a^2 = 0 \)⑥より, \( a = 0 \)
このとき\( 2a + b(\sqrt[3]{2})^2 + c\sqrt[3]{2} = 0 \)③は, \( c\sqrt[3]{2} = 0 \)となるので, \( c = 0 \)
(ii) \( ac = 0 \)すなわち\( a = 0 \)または\( c = 0 \)のとき,
(ii-i) \( a = 0 \)のとき, \( ac – b^2 = 0 \)⑤より, \( b = 0 \)
このとき\( 2a + b(\sqrt[3]{2})^2 + c\sqrt[3]{2} = 0 \)③は, \( c\sqrt[3]{2} = 0 \)となるので, \( c = 0 \)
(ii-ii) \( c = 0 \)のとき, \( ac – b^2 = 0 \)⑤より\( b = 0 \), \( bc – 2a^2 = 0 \)⑥より\( a = 0 \)
よって, \( a = b = c = 0 \)となるので, \( P(x) \)は\( x^3 – 2 \)で割り切れる。
振り返り
(1)は落としてはいけない。
(2)はやり方はわかっても, 式変形が難しい。本番では最後まで出来なくてもしょうがないが, よくあるテーマなので, 時間をかければできるようにしておくべき。
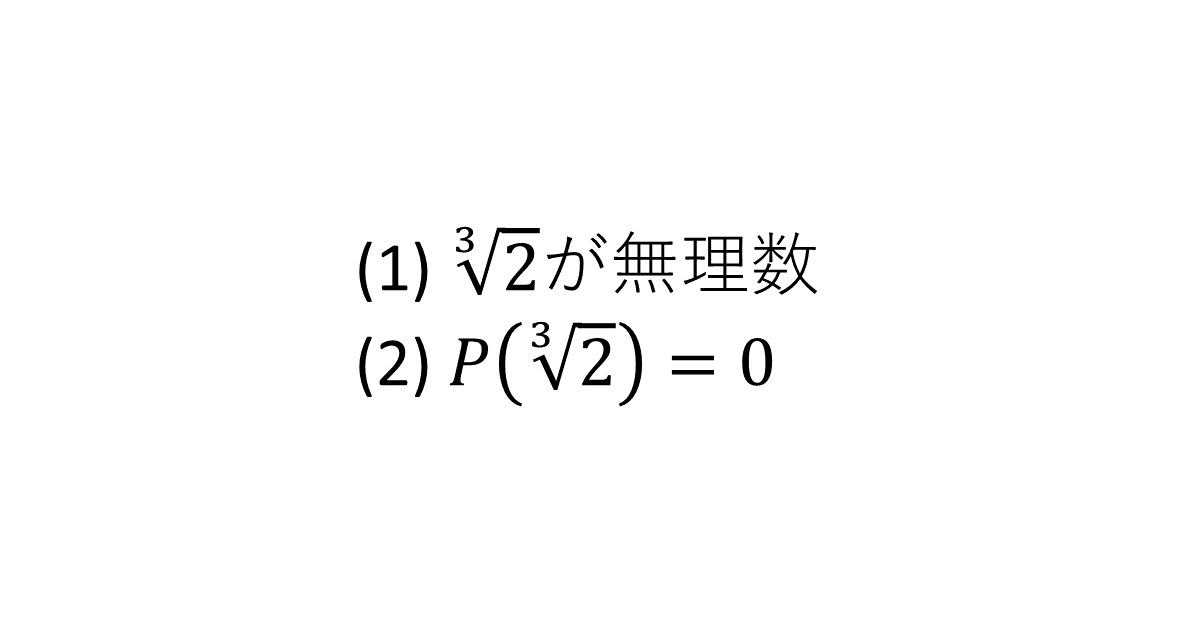
コメント