問題
\( n \)は\( 2 \)以上の自然数, \( p \)は素数, \( a_0, a_1, \cdots, a_{n-1} \)は整数とし, \( n \)次式
\( f(x) = x^n + pa_{n-1}x^{n-1} + \cdots + pa_ix^i + \cdots + pa_0 \)
を考える。
(1) 方程式\( f(x) = 0 \)が整数解\( \alpha \)を持てば, \( \alpha \)は\( p \)で割り切れることを示せ。
(2) \( a_0 \)が\( p \)で割り切れなければ, 方程式\( f(x) = 0 \)は整数解をもたないことを示せ。
発想
(1)は, 素直に\( x = \alpha \)を代入する。因数分解ができる。
(2)は, 「ならば」が入った命題の証明は, 常に対偶を意識しないといけない。この問題だと対偶を取ると(1)が使えるので, その方針で間違いないだろうと確信しつつ進める。
下書き
(1)
方程式\( f(x) = 0 \)に\( x = \alpha \)を代入してみると,
$$ \alpha^n + \color{red}{p}a_{n-1}\alpha^{n-1} + \color{red}{p}a_{n-2}\alpha^{n-2} + \cdots + \color{red}{p}a_2\alpha^2 + \color{red}{p}a_1\alpha + \color{red}{p}a_0 = 0 $$
\( \alpha^n \)以外を移項して\( \color{red}{p} \)でくくると,
$$ \alpha^n = -\color{red}{p}(a_{n-1}\alpha^{n-1} + a_{n-2}\alpha^{n-2} + \cdots + a_2\alpha^2 + a_1\alpha + a_0) $$
この式の括弧の中は整数で, \( p \)も\( \alpha^n \)も整数だから, \( \alpha^n \)は\( p \)の倍数となることが分かる。さらに, \( p \)は素数だから, \( \alpha \)は\( p \)の倍数となる。
(2)
対偶を取り, 「方程式\( f(x) = 0 \)は整数解をもつならば, \( a_0 \)が\( p \)で割り切れる」ことを示す。
方程式\( f(x) = 0 \)は整数解をもつとすると, (1)より, その整数解は\( p \)の倍数となる。よって, 整数解が\( x = pA \)(\( A \)は整数)とおける。
これを\( f(x) = 0 \)に代入すると,
$$ (pA)^n + pa_{n-1}(pA)^{n-1} + pa_{n-2}(pA)^{n-2} + \cdots + pa_2(pA)^2 + pa_1(pA) + pa_0 = 0 $$
\( p \neq 0 \)だから両辺\( p \)で割れて, \( a_0 \)だけを残すと残りの部分は\( p \)でくくれる。そのように整理すると,
$$ a_0 = -p(A^np^{n-2} + a_{n-1}A^{n-1}p^{n-2} + \cdots + a_2A^2p + a_1A) $$
(1)と同様に整数条件を使うと, \( a_0 \)は\( p \)の倍数と示せるので, 証明完了。
解答例
(1)
\( f(x) = 0 \)が整数解\( \alpha \)を持つとき, \( x = \alpha \)を代入して整理すると,
$$ \alpha^{n} = -p(a_{n-1}\alpha^{n-1} + a_{n-2}\alpha^{n-2} + \cdots + a_2\alpha^2 + a_1\alpha + a_0) $$
上式において, 括弧の中身, \( p \), \( \alpha^n \)は整数だから, \( \alpha^n \)は\( p \)の倍数である。よって, \( p \)は素数だから, \( \alpha \)も\( p \)の倍数, すなわち\( p \)で割り切れる。
(2)
\( f(x) = 0 \)は整数解をもつとすると, (1)より, その整数解は\( p \)の倍数となる。よって, 解を\( x = pA \)(\( A \)は整数)とおく。\( f(x) = 0 \)に代入して整理すると,
$$ a_0 = -p(A^np^{n-2} + a_{n-1}A^{n-1}p^{n-2} + \cdots + a_2A^2p + a_1A) $$
上式において, 括弧の中身, \( p \), \( a_0 \)は整数だから, \( a_0 \)は\( p \)の倍数である。
よって, \( f(x) = 0 \)が整数解をもつならば, \( a_0 \)は\( p \)の倍数である。
したがって, 対偶を考えて, \( a_0 \)が\( p \)で割り切れなければ, 方程式\( f(x) = 0 \)は整数解をもたない。
振り返り
簡単な問題。対偶は常に意識しておくこと。
補足
本問は, 「アイゼンシュタインの既約判定法」という定理に関連している。
これを使うと, 整数係数の多項式が因数分解できないことを示せる(大学受験で役に立つことはまずない)。
整数係数の多項式
\( P(x) = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0 \)
について, 以下の\( 3 \)条件をすべて満たす素数をひとつでも見つけられたら, \( P(x) \)は(整数の範囲で)因数分解できない。
・\( a_n \)は\( p \)の倍数ではない
・\( a_{n-1}, a_{n-2}, \cdots, a_1, a_0 \)は\( p \)の倍数である
・\( a_0 \)は\( p^2 \)の倍数ではない
よく見てみると, 表現は異なるが, 本問とほとんど同じことを言っていることが分かるだろう。
これを使えば, 例えば,
・\( x^3 + 3x^2 + 9x + 6 \)は, 因数分解できない(\( p=3 \))
・\( 5x^4 + 21x^3 + 7x + 7 \)は, 因数分解できない(\( p=7 \))
・\( 5x^4 + 21x^3 + 7x + 49 \)は, 判定不能(実際には因数分解できない)
・\( x^3 + 21x^2 + 55x + 3 \)は, 判定不能(実際には因数分解できる)
などが判定できる。
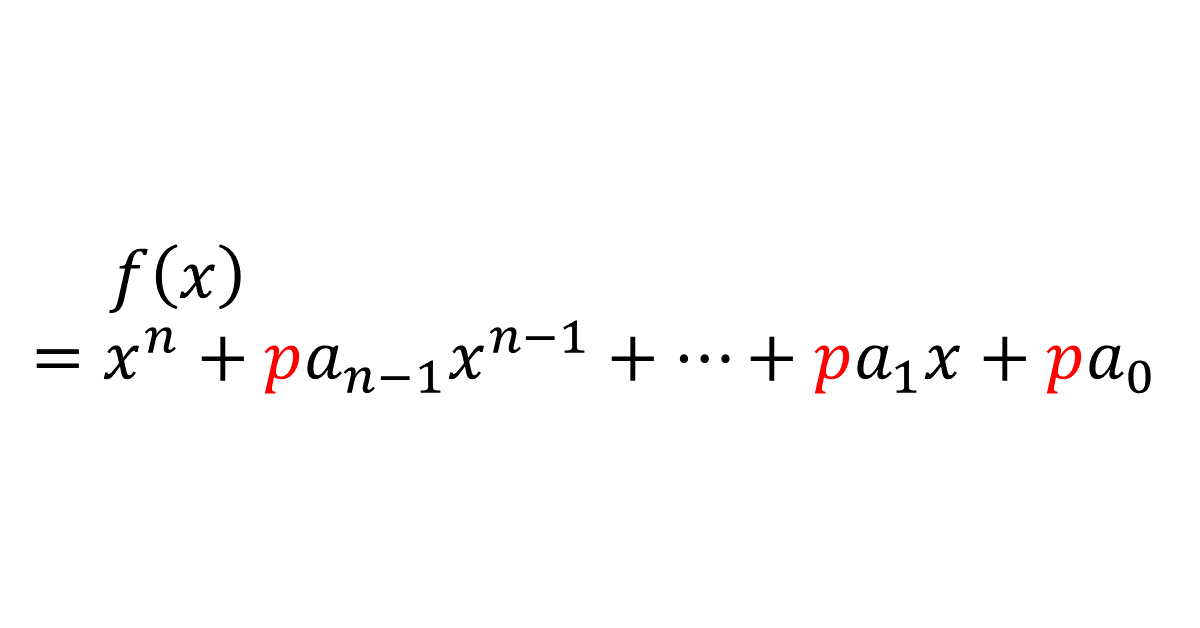
コメント