問題
\( n \)は\( 3 \)以上の自然数である。赤玉と白玉合わせて\( n \)個ずつ入ったつぼが\( \frac{n(n-1)}{2} \)個あり, その内訳は次のようになっている。各\( m=1, 2, \cdots, n-1 \)について, \( m \)個の赤玉と\( n-m \)個の白玉の入っているつぼがちょうど\( m \)個ある。いま, これらのつぼの\( 1 \)つの玉を無作為に取り出すとき, その玉が白玉である確率を求めよ。
発想
文字が多くてよく分からないので, まずは具体的に図を書く。
下書き
\( n=3, 4, 5 \)で図を書くと以下の通り(\( n=5 \)のときは多いので適度に省略している)。
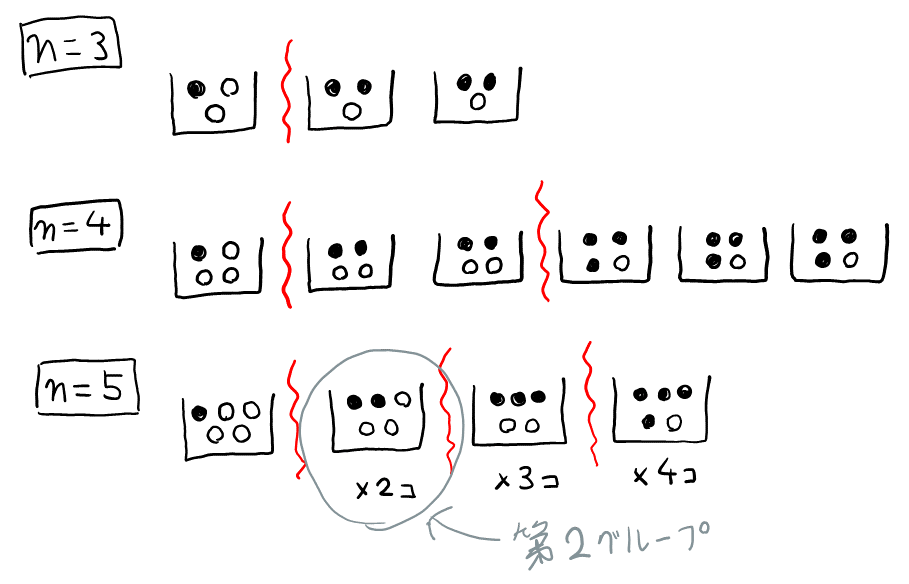
\( m \)ごとに同じつぼのグループに分けられそうなので, まず①第\( m \)グループのつぼを選び, 次に②そのグループのつぼから白玉を取り出す, と考える。
最後に, \( m \)を\( 1 \)から\( n-1 \)まで足し合わせればよい。
①第\( m \)グループのつぼを選ぶ確率
例えば\( n=5 \)のときの第\( 2 \)グループを選ぶ確率を考えると, つぼは全部で\( \color{red}{10} \)個, そのうち第\( 2 \)グループに属するつぼは\( \color{blue}{2} \)個なので, \( \frac{\color{blue}{2}}{\color{red}{10}} \)となる。
一般化すると, \( \color{red}{\frac{n(n-1)}{2}} \)個のつぼから\( \color{blue}{m} \)個のつぼを選ぶ確率なので, \( \frac{\color{blue}{m}}{\color{red}{\frac{n(n-1)}{2}}} \)。
②そのグループのつぼから白玉を選ぶ確率
例えば\( n=5 \)のときの第\( 2 \)グループのつぼはすべて, 赤玉\( 2 \)個と白玉\( \color{blue}{3} \)個の計\( \color{red}{5} \)個が入っているので, 白玉を選ぶ確率は, \( \frac{\color{blue}{3}}{\color{red}{5}} \)となる。
一般化すると, 赤玉\( m \)個と白玉\( \color{blue}{n-m} \)個の計\( \color{red}{n} \)個から白玉を選ぶ確率なので, \( \frac{\color{blue}{n-m}}{\color{red}{n}} \)。
\( m \)を足し合わせる
第\( m \)グループを選んで, かつそこから白玉を取り出す確率は, ①×②より, \( \frac{m}{\frac{n(n-1)}{2}} \times \frac{n-m}{n} = \frac{2m(n-m)}{n^2(n-1)} \)。
これら\( n-1 \)個の事象は排反(例えば\( m=1 \)のときと\( m=2 \)のときが同時に起こることはない)なので, 今度は足し算をすれば求める確率となる。よって, \( \displaystyle\sum_{m=1}^{n-1} \frac{2m(n-m)}{n^2(n-1)} \)を計算すればよい。
なお, 解答例では, シグマ計算を少し楽にするために, 赤玉を取り出す確率を求めて余事象を使った。
解答例
赤玉が\( m \)個入っているつぼ\( m \)個を, まとめてグループ\( m \)とする。
グループ\( m \)を選び, さらにそのつぼから赤玉を選ぶ確率を\( P(m) \)とすると,
$$P(m) = \frac{m}{\frac{n(n-1)}{2}} \times \frac{m}{n} = \frac{2m^2}{n^2(n-1)}$$
よって, 最終的に赤玉を取り出す確率は,
$$\begin{eqnarray}
\sum_{m=1}^{n-1} P(m) &=& \sum_{m=1}^{n-1}\frac{2m^2}{n^2(n-1)} = \frac{2}{n^2(n-1)} \sum_{m=1}^{n-1} m^2 \\
&=& \frac{2}{n^2(n-1)} \cdot \frac{1}{6} (n-1)n(2n-1) \\
&=& \frac{2n-1}{3n}
\end{eqnarray}$$
したがって, 求める確率は, 余事象を考えて, \( 1 – \frac{2n-1}{3n} = \frac{n+1}{3n} \)
別解
すべてのつぼに\( n \)個入っているということは, 全ての玉の取り出し方は同様に確からしいので, 「つぼを選ぶ→そのつぼから玉を1つ取り出す」という2段階に分けなくても, つぼを全て取り払って, 「すべての玉から1つ取り出す」と考えたときの確率は等しい。よって, 玉の総数と白玉の総数を求めればおしまい。
玉の総数\( N_{\rm{all}} \)は, もちろん\( n \times \frac{n(n-1)}{2} \)。白玉の総数\( N_{\rm{white}} \)は, \( \displaystyle\sum_{m=1}^{n-1} m \cdot (n-m) \)。
よって, \( \frac{N_{\rm{white}}}{N_{\rm{all}}} \)が求める確率となり, 計算すると\( \frac{n+1}{3n} \)と一致する。
振り返り
一般の\( n \)を使った問題は京大で頻出なので, 慣れておく必要がある。普通の人は最初から一般的な形で考えることは出来ないので, まずは具体的な例をよく観察して特徴を把握し, そこから抽象化した解答を書けるように訓練が必要。そこさえできれば難しい問題ではない。

コメント