問題
\( n, k \)は自然数で, \( n \geqq 3, k \geqq 2 \)を満たすものとする。いま, \( n \)角柱の\( n+2 \)個の面に\( 1 \)から\( n+2 \)までの番号が書いてあるものとする。この\( n+2 \)個の面に\( 1 \)面ずつ, 異なる\( k \)色の中から\( 1 \)色ずつ選んでは塗っていく。このとき, どの隣り合う面の組も同一色では塗られない塗り方の数を\( P_k \)で表す。
(1) \( P_2 \)と\( P_3 \)を求めよ。
(2) \( n=7 \)のとき, \( P_4 \)を求めよ。
発想
具体的に図を書いて, 題意を把握する。単なる塗り分けの問題なので, 例えば展開図などを書いて考える。あとは\( n \)や\( k \)の具体的な値が与えられているので, 最悪しらみつぶしで解けそうな問題。
下書き
\( n \)角柱の図は以下の通り。立体図で考えるとわかりにくいので, 展開図で考えると良い。太線のところは隣り合っていると考えてほしい。
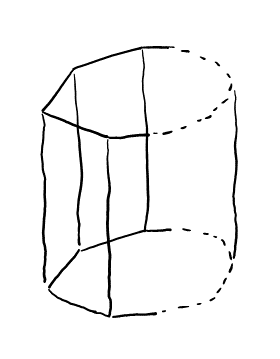
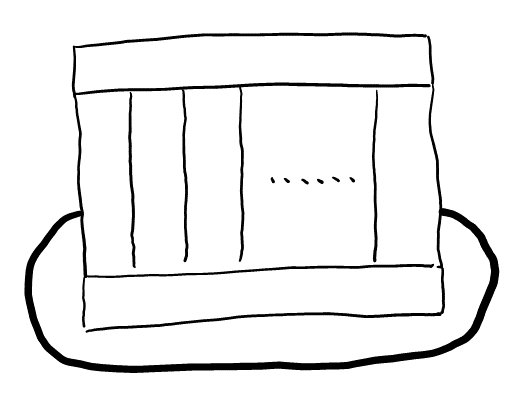
この図で, 隣り合う長方形が違う色になるように塗り分ける。
(1)\( P_2 \)
\( 2 \)色以内で塗り分ける。\( 2 \)色しか使えなかったら, ほぼ明らかに無理そう。使う色を, 色①, 色②とする。
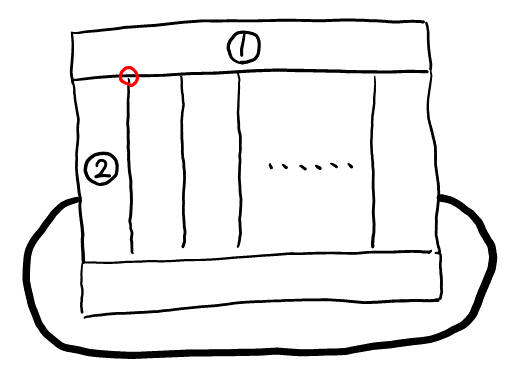
図のように順に塗っていくと, これ以上塗れなくなる。記述では, 「\( 3 \)面を共有する頂点があるので」くらいで書いておけば良いだろう(図の赤点部分)。
(1)\( P_3 \)
\( 3 \)色以内で塗り分ける。使う色を, 色①, 色②, 色③とする。順番に塗っていくと, 以下の通り。
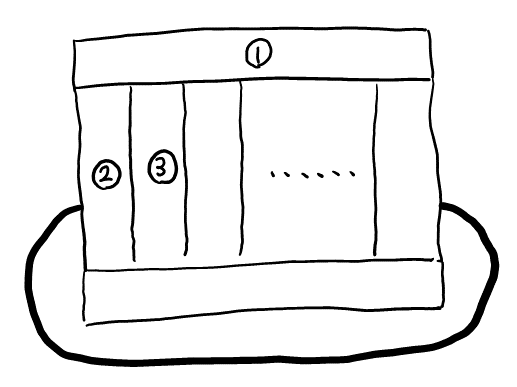
ここから, 底面を考えると, ②③は接しているので①しか塗れない。残りの側面も②③②③の順で塗っていくしかない。
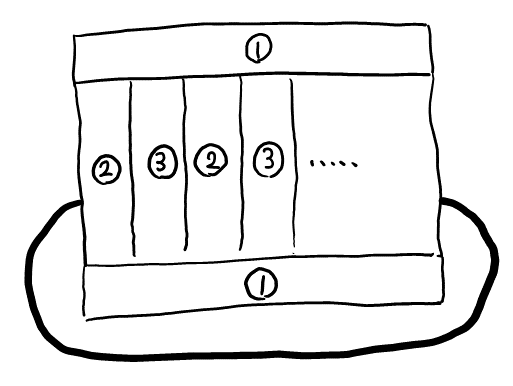
あとは, 太線部分で同じ色にならないようにだけ注意すると, 側面の数が奇数のとき, ②③ ②③ … ②③ ②となってしまって②の色が隣り合ってしまう。よって, どう頑張っても塗り分けられない。
側面の数が偶数のときは, ②③ ②③ … ②③となって, きれいに塗り分けることができる。色①②③を使う塗り方はこの\( 1 \)通りだけなので, 色の選び方を考えると, \( 1 \times 3! \)通り。
(2)
\( 7 \)角柱を\( 4 \)色以内で塗り分ける。(1)より, \( 3 \)色では塗り分けられないので, \( 4 \)色すべて使うことになる。使う色を, 色①, 色②, 色③, 色④とする。
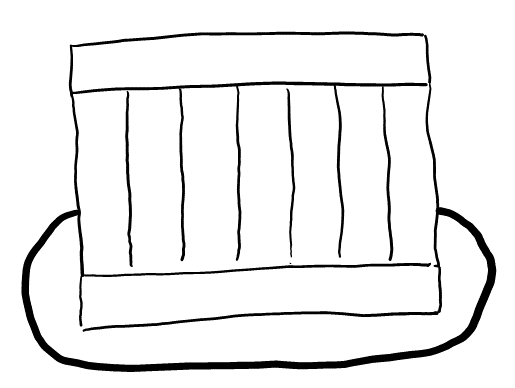
側面の数が奇数なので, (1)より, 側面を\( 2 \)色で塗り分けることは出来ない。よって, 側面に\( 3 \)色以上必要。もちろん\( 4 \)色使うと上面(底面)に使う色が無くなるので, 側面に使う色は\( 3 \)色に確定。この塗り方を数えればよい。注意することは, 最初と最後の色が同じにならないことだけである。
これまでの考察から, 以下の図までは確定。
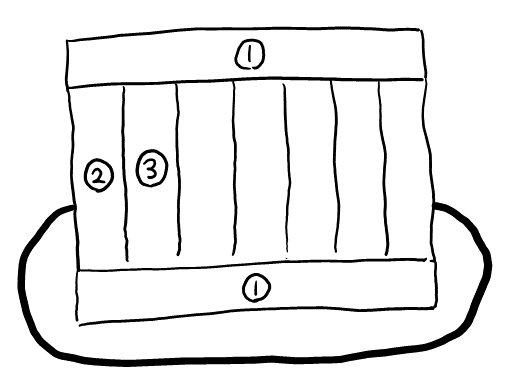
残り\( 5 \)つの側面を, 隣り合わないように②③④で塗り, 最後が②にならない塗り方を求める。ここまでくれば樹形図でなんとかなるだろう。
隣り合わないためにはそれぞれの面に\( 2 \)通りの塗り方が考えられるので最大で\( 2^5 = 32 \)通りであり, 樹形図を全部書いてそこから最後が②になる場合を引いても大した手間ではない。最後の方だけ気を付ければよいので, 多少省略すると以下のように書けて, \( 21 \)通りだとわかる。
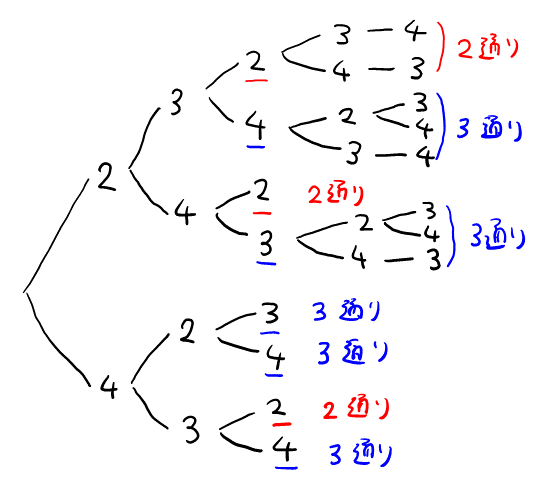
最後に色の選び方を考えて, \( 21 \times 4! \)通り。
解答例
(1)
\( n \)角柱の各頂点は\( 3 \)面を共有するので, \( 2 \)色では塗り分けられない。よって, \( P_2 = 0 \)。
また, \( 3 \)色使うとき, 上面と底面は同じ色である必要がある。その色を①とする。このとき, 側面のある\( 1 \)面の色を②とする。残りの色を③とすると, その側面から順に, ③②③②…と交互に塗っていくと, 側面の数が奇数のときは同じ色が接してしまうが, 側面の数が偶数のときは塗り分けることができる。よって, 色①②③の選び方は\( 3! = 6 \)通りあるので, \( n \)が奇数のとき\( P_3 = 0 \), \( n \)が偶数のとき\( P_3 = 6 \)。
(2)
(1)より\( 7 \)角柱は\( 3 \)色では塗り分けられないので\( 4 \)色使うことになり, その色を①②③④とする。
上面と底面は同じ色である必要がある。その色を①とする。このとき, 側面のある\( 1 \)面の色を②, その隣の色を③とする。残り\( 5 \)面を同じ方向に順に塗っていくと考える。最後の面の色が②にならないように注意して樹形図を書くと, その塗り方は\( 21 \)通りある(樹形図は省略)。
よって, 色①②③④の選び方は\( 4! = 24 \)通りあるので, \( P_4 = 24 \times 21 = 504 \)。
振り返り
塗分け問題は苦手な人も多いので差が付いたかもしれない。基本的なやり方は確立しておこう。
(2)では, 塗り分けの条件を絞っていくと, \( 5 \)面の塗り分けに落とし込めるところがポイント。そこに必然的に至るまでのロジックにも注目してほしい。そのあとは樹形図以外にもやり方は考えられるが, しらみつぶしが一番間違いが少ないだろう。

コメント