問題
すべては\( 0 \)ではない\( n \)個の実数\( a_1, a_2, \cdots, a_n \)があり, \( a_1 \leqq a_2 \leqq \cdots \leqq a_n \)かつ\( a_1 + a_2 + \cdots + a_n = 0 \)を満たすとき, \( a_1 + 2a_2 + \cdots + na_n >0 \)が成り立つことを証明せよ。
発想
題意が分かりにくいので, まずは小さい\( n \)で具体的な状況を把握する。そのあとは, そのイメージを活用して上手く式変形をするか, \( n \)についての命題なので, 数学的帰納法も考えられる。
下書き
式変形で示す
\( n = 1 \)のときは\( a_1 = 0 \)だが, これは「すべては\( 0 \)ではない」という条件に反する。よって, \( n \geqq 2 \)で考える。
\( n = 2 \)のときは, \( a_1 \leqq a_2 \)かつ\( a_1 + a_2 = 0 \)。2式から\( a_2 \)を消去すると, \( a_1 \leqq 0 \)。ここで\( a_1 = 0 \)とすると\( a_2 \)も\( 0 \)になってしまうから, 条件に反する。よって, \( a_1 < 0 \)。
このとき, \( a_1 + 2a_2 = -a_1 > 0 \)が確かに成り立つ。
\( n = 3 \)のときは, \( a_1 \leqq a_2 \leqq a_3 \)かつ\( a_1 + a_2 + a_3 = 0 \)。2式から\( a_3 \)を消去して頑張ると, \( a_1 + 2a_2 + 3a_3 \geqq 0 \)が言えるが, イコールの処理が厄介。
このように文字消去で, 一般の\( n \)で示すのはかなり厳しそう。別の方法を考える。
そもそも\( a_1 + 2a_2 + \cdots + na_n >0 \)が成り立つのは, 感覚的にほぼ明らかだと思えるだろうか。視覚的にイメージするために, 無理やり図を書くと, 以下のようになる。
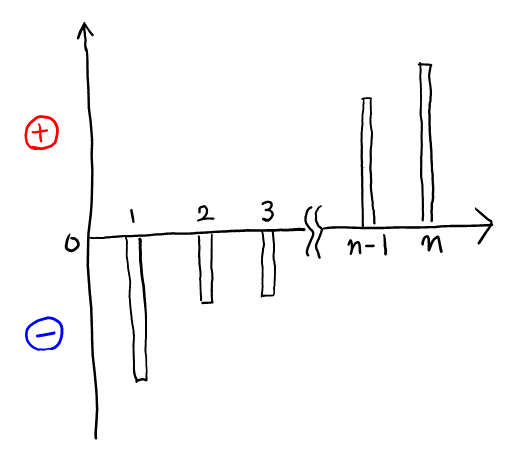
\( a_1 \leqq a_2 \leqq \cdots \leqq a_n \)より, 棒は小さい順に並び, \( a_1 + a_2 + \cdots + a_n = 0 \)より, 棒は上下の”バランス”が取れている(例えばマイナス側で極端に大きな棒があれば, プラス側でそれを打ち消している)。このような状態で, \( a_1 + 2a_2 + \cdots + na_n \)を考えると, 右に行くほど2倍3倍と”重要度”が大きくなっていくのだから, 全体では当然プラスになるだろう。
示すべき式は, 以下のように, マイナスの部分とプラスの部分に分けられる。
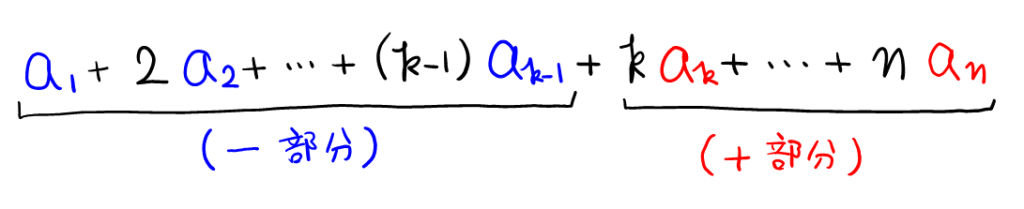
\( \color{blue}{(-部分)} + \color{red}{(+部分)} > 0 \)を示したいので, まずは\( \color{blue}{(-部分)} > ? \), \( \color{red}{(+部分)} > ? \)のように, それぞれ別々に式変形ができないかを考える。マイナスが入るとややこしいので, プラスの方から。\( \color{red}{(+部分)} \)は以下のように, 小さいものを\( k \)に合わせるか, \( a_k \)に合わせるかの2通りに変形できる。
$$\begin{eqnarray}
&& k\color{red}{a_k} + (k+1)\color{red}{a_{k+1}} + \cdots n\color{red}{a_n} \\
&>& ka_k + ka_{k+1} + \cdots + ka_n \\
&=& k(a_k + a_{k+1} + \cdots + a_n) …①
\end{eqnarray}$$
$$\begin{eqnarray}
&& k\color{red}{a_k} + (k+1)\color{red}{a_{k+1}} + \cdots n\color{red}{a_n} \\
&\geqq& ka_k + (k+1)a_k + \cdots na_k \\
&=& a_k(k + k+1 + \cdots + n)
\end{eqnarray}$$
ここは, 条件式\( a_1 + a_2 + \cdots + a_n = 0 \)があることを考慮して, 前者が良い変形となる。
これを意識して, \( \color{blue}{(-部分)} \)を以下のように変形する(\( \color{blue}{a_{●}} \)はすべて負であることに注意)。
$$\begin{eqnarray}
&& \color{blue}{a_1} + 2\color{blue}{a_2} + \cdots (k-1)\color{blue}{a_{k-1}} \\
&>& (k-1)a_1 + (k-1)a_2 + \cdots + (k-1)a_{k-1} \\
&=& (k-1)(a_1 + a_2 + \cdots + a_{k-1}) \\
&>& k(a_1 + a_2 + \cdots + a_{k-1}) …②
\end{eqnarray}$$
①と②を足すと, \( a_1 + 2a_2 + \cdots + na_n > k(a_1 + a_2 + \cdots + a_n) = 0 \)となる。
答案を書く際の注意点を一つ。\( \color{blue}{(-部分)} \)と\( \color{red}{(+部分)} \)の間に, \( (\pm 0部分) \)があるかもしれない。この場合は, ①式や②式の\( > \)が\( \geqq \)になる可能性がある。しかし, いずれにせよ②式の最後で必ずイコールが外れるので, 迷ったらイコールを含めておけばよい。
数学的帰納法で示す
書きやすさのため, 示すべき命題を, 変数\( n \)を使って,
\( P(n) \):「すべては\( 0 \)ではない\( n \)個の実数\( a_1, a_2, \cdots, a_n \)について, \( a_1 \leqq a_2 \leqq \cdots \leqq a_n \)かつ\( a_1 + a_2 + \cdots + a_n = 0 \)ならば, \( a_1 + 2a_2 + \cdots + na_n > 0 \)」
と定義しておく。\( n=2 \)のときは普通に示せるので, 「\( n=k \)のときに成り立つと仮定して\( n=k+1 \)のときを示す」部分を説明する。
示すべき命題は, \( P(k+1) \)である。ここで, 命題\( P(n) \)は, 「○→△」というように, 「ならば」が入っていることに注意してほしい。よって, \( P(k) \)の命題だけでなく, \( P(k+1) \)の仮定(○の部分)も使って, \( P(k+1) \)の結論(△の部分)を示すことになる。
つまり, \( k+1 \)個の実数がポンっと与えられて, それらが\( a_1 \leqq a_2 \leqq \cdots \leqq a_k \leqq a_{k+1} \)かつ\( a_1 + a_2 + \cdots + a_k + a_{k+1} = 0 \)を満たしている。さらに, \( P(k) \)の命題が成り立つこともわかっている。このとき, \( a_1 + 2a_2 + \cdots + ka_k + (k+1)a_{k+1} > 0 \)を示せ, ということである。
\( P(k) \)を改めて書くと,
「すべては\( 0 \)ではない\( k \)個の実数\( a_1, a_2, \cdots, \underline{a_k} \)について, \( a_1 \leqq a_2 \leqq \cdots \leqq \underline{a_k} \)かつ\( a_1 + a_2 + \cdots + \underline{a_k} = 0 \)ならば, \( a_1 + 2a_2 + \cdots + k\underline{a_k} > 0 \)」
となる。これは\( k \)個の実数に対する命題なので, 今考えている\( k+1 \)個の実数には, 直接用いることは出来ない。最後の2つ(\( a_k \)と\( a_{k+1} \))をまとめて1つと考えてやると,
「すべては\( 0 \)ではない\( k \)個の実数\( a_1, a_2, \cdots, \underline{(a_k+a_{k+1})} \)について, \( a_1 \leqq a_2 \leqq \cdots \leqq \underline{(a_k+a_{k+1})} \)かつ\( a_1 + a_2 + \cdots + \underline{(a_k+a_{k+1})} = 0 \)ならば, \( a_1 + 2a_2 + \cdots + k\underline{(a_k+a_{k+1})} > 0 \)」
という形で使えそうである。
実際に, \( a_1 \leqq a_2 \leqq \cdots \leqq (a_k+a_{k+1}) \)かつ\( a_1 + a_2 + \cdots + (a_k+a_{k+1}) = 0 \)が成り立っていることはすぐにわかる。
よって, \( a_1 + 2a_2 + \cdots + k(a_k+a_{k+1}) > 0 \)が言える。最終的な結論(\( P(k+1) \)の△の部分)は, \( a_1 + 2a_2 + \cdots + ka_k + (k+1)a_{k+1} > 0 \)だったが, ここまでくればほぼ自明である。
解答例1
\( n = 1 \)のとき, \( 0 \)ではない実数\( a_1 \)が\( a_1 = 0 \)を満たすことはないので, \( n \geqq 2 \)で考える。
条件より, \( a_1 < 0 \)かつ\( a_n > 0 \)だから, \( a_1 \leqq \cdots \leqq a_{k-1} \leqq 0 \leqq a_k \leqq \cdots a_n \)を満たす\( k \)が存在する。このとき,
\( a_1 + \cdots + (k-1)a_{k-1} > k(a_1 + a_2 + \cdots + a_{k-1}) \),
\( ka_k + \cdots + na_n \geqq k(a_k + \cdots a_n) \)
が成り立つので, \( a_1 + 2a_2 + \cdots + na_n > k(a_1 + \cdots + a_n) = 0 \)が成り立つ。
解答例2
\( n = 1 \)のとき, \( 0 \)ではない実数\( a_1 \)が\( a_1 = 0 \)を満たすことはないので, \( n \geqq 2 \)で考える。
\( P(n) \):「すべては\( 0 \)ではない\( n \)個の実数\( a_1, a_2, \cdots, a_n \)について, \( a_1 \leqq a_2 \leqq \cdots \leqq a_n \)かつ\( a_1 + a_2 + \cdots + a_n = 0 \)ならば, \( a_1 + 2a_2 + \cdots + na_n > 0 \)」とおく。
(i) \( n = 2 \)のとき, \( P(2) \)の仮定より, \( a_1 \leqq a_2 \)かつ\( a_1 + a_2 = 0 \)。よって, \( a_1 \leqq 0 \)。
ここで\( a_1 = 0 \)とすると\( a_2 \)も\( 0 \)となり, 条件に反する。よって, \( a_1 < 0 \)。
このとき, \( a_1 + 2a_2 = -a_1 > 0 \)となるので, \( P(2) \)は真である。
(ii) \( n = k \)のとき\( P(k) \)が真と仮定し, すべては\( 0 \)ではない\( k+1 \)個の実数\( a_1, \cdots, a_{k+1} \)が, \( a_1 \leqq \cdots \leqq a_{k+1} \)かつ\( a_1 + \cdots + a_{k+1} = 0 \)を満たしているとする。すべては\( 0 \)ではないので\( a_{k+1} > 0 \)となり, したがって\( a_k \leqq a_k + a_{k+1} \)である。
このとき, \( k \)個の実数\( a_1, a_2, \cdots, a_{k-1}, (a_k+a_{k+1}) \)について考えると, \( a_1 \leqq a_2 \leqq \cdots \leqq a_{k-1} \leqq (a_k+a_{k+1}) \)かつ\( a_1 + a_2 + \cdots + a_{k-1} + (a_k+a_{k+1}) = 0 \)を満たしていることになる。
(ii-i) \( k \)個の実数\( a_1, a_2, \cdots, a_{k-1}, (a_k+a_{k+1}) \)がすべては\( 0 \)ではないとき, \( P(k) \)が真であるとの仮定から, \( \underline{a_1 + 2a_2 + \cdots + k(a_k+a_{k+1})} > 0 \)となる。このとき,
$$\begin{eqnarray}
&& a_1 + 2a_2 + \cdots + ka_k + (k+1)a_{k+1} \\
&>& \underline{a_1 + 2a_2 + \cdots + ka_k + ka_{k+1}} (\because a_{k+1} > 0) \\
&>& 0
\end{eqnarray}$$
(ii-i) \( k \)個の実数\( a_1, a_2, \cdots, a_{k-1}, (a_k+a_{k+1}) \)がすべて\( 0 \)のとき,
$$\begin{eqnarray}
&& a_1 + 2a_2 + \cdots + ka_k + (k+1)a_{k+1} \\
&=& ka_k + (k+1)a_{k+1} (\because a_1 = \cdots = a_{k-1} = 0)\\
&=& -ka_{k+1} + (k+1)a_{k+1} (\because a_k+a_{k+1} = 0)\\
&=& a_{k+1} \\
&>& 0
\end{eqnarray}$$
よって, \( P(k) \)が真と仮定したときに, \( P(k+1) \)も真となる。
(i)(ii)より, 任意の\( n \)について, \( P(n) \)が成り立つ。
振り返り
一般に不等式は, 式変形の候補が無限に考えられるので, 正しい式変形をすることが難しいことが多い。解答例1は, 解答例2と比べて記述量が非常に少なく洗練されているが, この解答を書くにはかなりの訓練が必要である。
一方解答例2は, 帰納法を使うということさえ思いつけば, あとはほぼ機械的に解答可能である。ただしその場合も, 帰納法の仕組みをしっかりと理解し, どの仮定を使ってどの結論を言うのかを明確にしないと, 頭が混乱してしまう。京大では帰納法は頻出なので, 本問のような少し変化球の場合でも, 正しく帰納法を適用する練習をしておきたい。
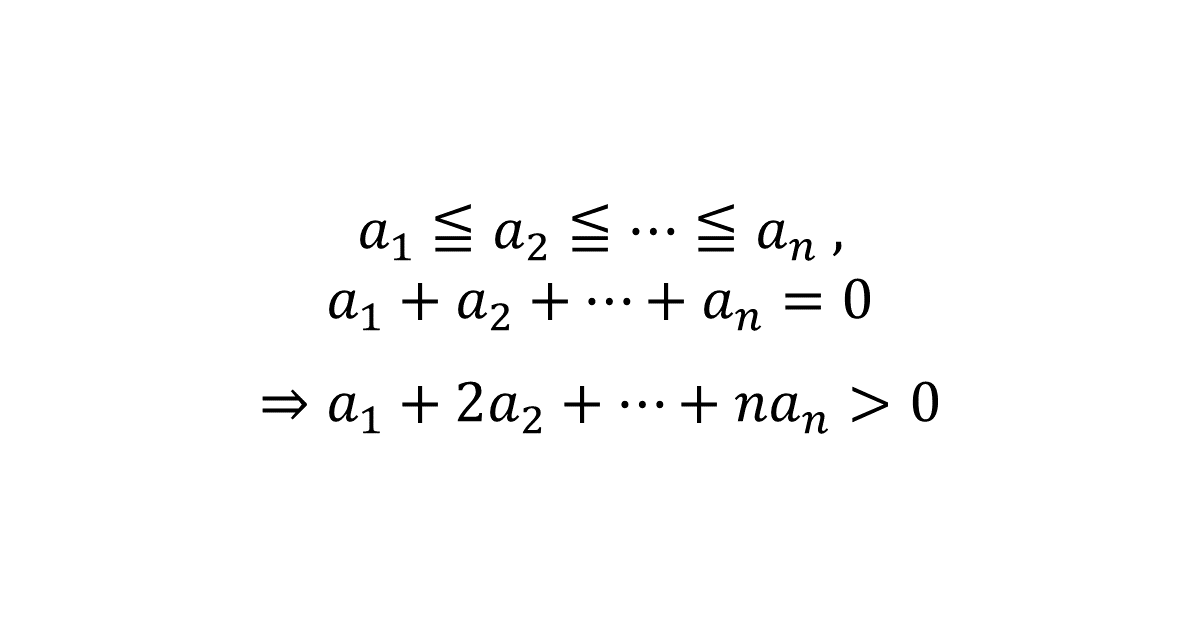
コメント