問題
次の文を読んで, に適した式を, また{ }の中の語句の正しいものの番号を, それぞれの解答欄に記入せよ。計算においては, 絶対値が\( 1 \)に比べて十分小さい量\( \varepsilon \)に対して\( \frac{1}{1 + \varepsilon} \fallingdotseq 1 – \varepsilon \), \( (1 + \varepsilon)^2 \fallingdotseq 1 + 2\varepsilon \)の近似を使うことができるものとする。
(1)
図のように質量が\( m \)で大きさの無視できる小物体\( \rm{A} \)が, 質量の無視できるひもでつながれて, 水平におかれた板の上を半径\( r \)で等速円運動している。ひもは, 大きさの無視できる穴を通して鉛直下方に引かれ, ひもの端点\( \rm{P} \)ははじめ固定されている。小物体\( \rm{A} \)と板の間の摩擦, ひもと板, ひもと穴の間の摩擦, および空気抵抗はないものとする。
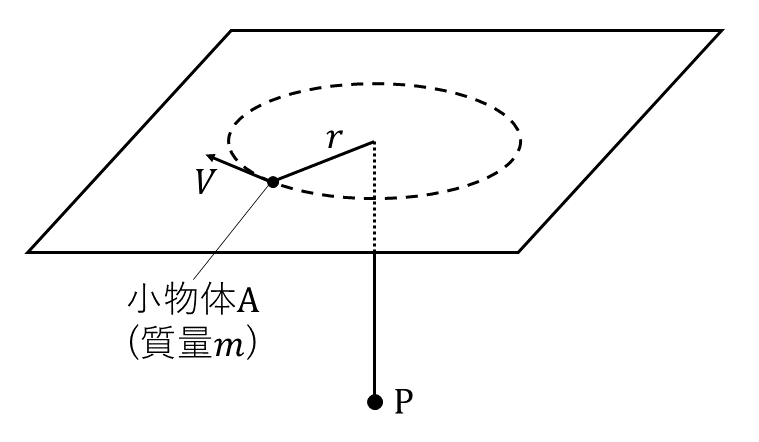
円運動をしている小物体\( \rm{A} \)の, 円周方向の速さを\( V \)とすると, ひもの張力\( T \)は\( T = \)イで与えられる。いま, このひもの端点\( \rm{P} \)をゆっくりと\( \varDelta r \)だけ引き, 小物体\( \rm{A} \)が半径\( r – \varDelta r \)の等速円運動に移る過程を考える。ここで\( \varDelta r \)は\( r \)に比べて十分小さい正の量とする。この過程において, 小物体\( \rm{A} \)の得るエネルギーは\( T \times \varDelta r \)と見なすことができる。このエネルギーは小物体\( \rm{A} \)の運動エネルギー\( E = \frac{mV^2}{2} \)の増分\( \varDelta E \)に外ならない。そこで\( \varDelta E \)と\( E \)の比を, \( r \)と\( \varDelta r \)を用いて表すと\( \frac{\varDelta E}{E} = \)ロとなる。
この過程において, 円運動をしている小物体\( \rm{A} \)の速さが\( V \)から\( V + \varDelta V \)に変わったとすると, 運動エネルギーは\( \frac{m(V + \varDelta V)}{2} \)となる。ここで\( \frac{\varDelta V}{V} \)は\( 1 \)に比べて十分小さい量と考えられるので, \( (\frac{\varDelta V}{V})^2 \)の項を無視できるとすると, 運動エネルギー\( E \)の増分\( \varDelta E \)はハ\( \times \varDelta V \)である。したがって速さの変化\( \varDelta V \)は, \( V, r, \varDelta r \)を用いて\( \varDelta V = \)ニ\( \times \varDelta r \)となる。\( r \)と\( V \)が変化することにより, 小物体\( \rm{A} \)の回転の角速度\( \omega = \frac{V}{r} \)も\( \omega + \varDelta \omega \)に変化する。\( \frac{\varDelta r}{r}, \frac{\varDelta V}{V} \)が\( 1 \)に比べて十分小さいことを考慮して, はじめに述べた近似式を用い, \( \frac{\varDelta \omega}{\varDelta r} \)を\( V \)と\( r \)を用いて表すと\( \frac{\varDelta \omega}{\varDelta r} = \)ホとなる。ロとニを導く過程から, \( \frac{\varDelta E}{E} = \frac{\varDelta \omega}{\omega} \)が成り立っていることがわかる。したがって\( \frac{\omega + \varDelta \omega}{E + \varDelta E} \)は, \( E \)と\( \omega \)を用いてヘと表すことができる。ゆえに, この過程で小物体\( \rm{A} \)の運動エネルギー\( E \)および角速度\( \omega \)はともに増加し, \( \frac{\omega}{E} \)は{ト:① 増加する。 ② 一定である。 ③ 減少する。}
(2)
次に, 最初の状態で張力\( T \)にちょうどつりあう力を与える質量\( M \)のおもり\( \rm{B} \)を, 端点\( \rm{P} \)にとりつけ, おもり\( \rm{B} \)は静止しているとする。重力加速度を\( g \)とすると, このとき小物体\( \rm{A} \)の回転半径\( r \)は, \( m, M, g, V \)を用いて, \( r = \)チ\( \times V^2 \)と表される。おもり\( \rm{B} \)を手で静止位置から\( \varDelta r \)が\( r \)に比べて十分小さいとして\( \varDelta r \)だけゆっくりと鉛直下方に下げてから静かに離すと, おもり\( \rm{B} \)にはもとの静止位置に向けて上向きに大きさ\( F \)の力が働く。\( \varDelta r \)が\( r \)に比べて十分小さいとして\( \varDelta r \)に比例する項だけを考え, \( F = k \times \varDelta r \)としよう。\( k \)は\( M, g, r \)を用いて表すとリとなる。よって\( \varDelta r \)の移動に対してこのおもりに働く力は, ばねの弾性力に類似していることがわかる。このおもり\( \rm{B} \)はもとの静止位置を中心に上下に振動する。おもり\( \rm{B} \)の運動は小物体\( \rm{A} \)の回転運動に比べて非常にゆっくりしているとする。このおもり\( \rm{B} \)の上下振動の振動数\( f \)を\( k \)と\( M \)で表すと\( f = \)ヌとなる。
解説
文中に与えられた近似について確認しておく。前者は\( \frac{1}{1 + \varepsilon} = (1 + \varepsilon)^{-1} \fallingdotseq 1 – \varepsilon \)であり, 後者は\( (1 + \varepsilon)^\alpha = 1 + \alpha \varepsilon \)の形そのものである。よっていつもの一次近似であるから, 与えられた式の形にこだわる必要はなく, また微小量同士の掛け算もすべて無視してよい。
(1)
イ
円運動の公式そのもの。
ロ
「運動エネルギーの変化=外力のした仕事」だから, \( \varDelta E = T \times \varDelta r \)が成り立つ, と説明されている。これに従って\( \varDelta E \)を計算すればよいだけ。
ハ
ロではエネルギーと仕事の関係から\( \varDelta E \)を求めたが, ここでは直接\( \varDelta E \)を求める。「変化量 = 後 – 前」。
前:\( E = \frac{mV^2}{2} \)
後:\( E + \varDelta E = \frac{m(V + \varDelta V)^2}{2} = \frac{m(V^2 + 2V \varDelta V)}{2} \)(\( (\varDelta V)^2 \)は無視)
辺々引くと, \( \varDelta E = mV \varDelta V \)。
ニ
ロとハで別々の方法で\( \varDelta E \)を求めたので, 等式を立てるのが定石。
ホ
前:\( \omega = \frac{V}{r} \)
後:\( \omega + \varDelta \omega = \frac{V + \varDelta V}{r – \varDelta r} \)
より, まずは\( \varDelta \omega \)が求められそう。その前に\( \frac{V + \varDelta V}{r – \varDelta r} \)を変形しておくと, 以下のようになる(与えられた近似式を使ってもよいが, より汎用的な以下の式変形を身に付けておくこと)。
$$\begin{eqnarray}
\frac{V + \varDelta V}{r – \varDelta r} &=& (V + \varDelta V)(r – \varDelta r)^{-1} \\
&=& \left\{ V\left(1 + \frac{\varDelta V}{V}\right) \right\}\left\{ r\left(1 – \frac{\varDelta r}{r}\right) \right\}^{-1} \\
&=& Vr^{-1}\left(1 + \frac{\varDelta V}{V}\right)\color{red}{\left(1 – \frac{\varDelta r}{r}\right)^{-1}} \\
&=& \frac{V}{r}\left(1 + \frac{\varDelta V}{V}\right)\left(\color{blue}{1 + \frac{\varDelta r}{r}}\right)(\because 一次近似式\color{red}{(1 + \varepsilon)^\alpha} = \color{blue}{1 + \alpha \varepsilon}) \\
&=& \frac{V}{r}\left(1 + \frac{\varDelta V}{V} + \frac{\varDelta r}{r}\right)(\because \varDelta V \varDelta rの項は無視できる)
\end{eqnarray}$$
よって辺々引くと, \( \varDelta \omega = \frac{V}{r}(\frac{\varDelta V}{V} + \frac{\varDelta r}{r}) \)
\( \varDelta V \)と\( \varDelta r \)の関係式はニで求めたので\( \varDelta V \)が消去でき, 最後に\( \varDelta r \)で割れば確かに\( V \)と\( r \)だけで表せる。
ヘ
ロとニを導く過程から, というのがよく分からなくても, とにかく\( \frac{\varDelta E}{E} = \frac{\varDelta \omega}{\omega} \)を使って良いらしいので, \( \frac{\varDelta E}{E} \)や\( \frac{\varDelta \omega}{\omega} \)を作ることを意識して式変形していく。
$$\begin{eqnarray}
\frac{\omega + \varDelta \omega}{E + \varDelta E}
&=& \frac{\omega\left(1 + \frac{\varDelta \omega}{\omega}\right)}{E\left(1 + \frac{\varDelta E}{E}\right)} \\
&=& \frac{\omega}{E}\left(\because \frac{\varDelta E}{E} = \frac{\varDelta \omega}{\omega}\right)
\end{eqnarray}$$
ト
直観的に答えは②(一定である)としてしまってよい。最初の状態\( \frac{\omega}{E} \)から微小に変化させた\( \frac{\omega + \varDelta \omega}{E + \varDelta E} \)は, \( \frac{\omega}{E} \)と等しく, 以下同様に, 微小に変化させていっても, 結局\( \frac{\omega}{E} \)のまま一定となるのはほぼ明らかである。
(2)
チ, リ
前:\( T = m\frac{V^2}{r} (=Mg) \)
後:\( T’ = m\frac{(V + \varDelta V)^2}{r – \varDelta r} \)
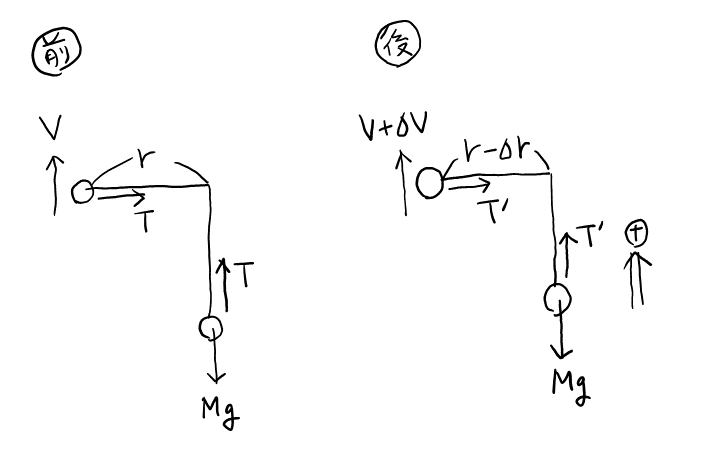
図より, 鉛直上向きを正とすると, \( F = T’ – Mg \)だから, 辺々引けばよい。
その前に\( T’ \)を変形しておくと, 以下のようになる。
$$\begin{eqnarray}
T’ &=& m\frac{(V + \varDelta V)^2}{r – \varDelta r} \\
&=& m(V + \varDelta V)^2(r – \varDelta r)^{-1} \\
&=& m \left\{V \left(1 + \frac{\varDelta V}{V}\right)\right\}^2 \left\{r \left(1 – \frac{\varDelta r}{r}\right)\right\}^{-1} \\
&=& m V^2 r^{-1} \left(1 + \frac{\varDelta V}{V}\right)^2 \left(1 – \frac{\varDelta r}{r}\right)^{-1} \\
&=& m\frac{V^2}{r} \left( 1 + 2\frac{\varDelta V}{V} \right) \left( 1 + \frac{\varDelta r}{r} \right) (\because 一次近似式) \\
&=& m\frac{V^2}{r} \left( 1 + 2\frac{\varDelta V}{V} + \frac{\varDelta r}{r} \right) (\because \varDelta V \varDelta rの項は無視できる)
\end{eqnarray}$$
辺々引くと, \( m\frac{V^2}{r} \)の項が消えるので, \( F = m\frac{V^2}{r} \left( 2\frac{\varDelta V}{V} + \frac{\varDelta r}{r} \right) \)。
\( \varDelta V \)と\( \varDelta r \)の関係式はニで求めたので\( \varDelta V \)が消去でき, \( F = m\frac{V^2}{r} \cdot 3\frac{\varDelta r}{r} \)となる。
あとは\( m\frac{V^2}{r} =Mg \)の関係式を適当に使って終了。
ヌ
単振動の典型問題。この角振動数を\( \omega’ \)とすると, \( \omega’ = \sqrt{\frac{k}{M}} \)(公式扱い)であり, \( \omega’ = 2\pi f \)(こちらも当然覚えておく)の関係式から\( f \)が出てくる。
振り返り
難易度は標準的だが, 式が散らかって何を使えばよいのかわからなくなったり, 計算ミスしたりで, 最後までできなかった人も多いと思う。流れを意識すると次にやることが見えてきやすい。
また, 慣れるまでは近似計算が大変かもしれない。\( \frac{V + \varDelta V}{r – \varDelta r} \)や\( \frac{(V + \varDelta V)^2}{r – \varDelta r} \)のような形を見たら, 息を吸うように近似したい。一次近似式の適用方法や式変形はある種の型があり, 過去問演習を積んでいけば自ずと慣れるはずである。
(2)のチとヌは, それぞれ独立に解けるので, これらに手を付けず途中でギブアップしてしまった人は要注意。
コメント