問題
\( k \)は\( 0 \)または正の整数とする。方程式\( x^2 – y^2 = k \)の解\( (a, b) \)で, \( a, b \)がともに奇数であるものを奇数解とよぶ。
(1) 方程式\( x^2 – y^2 = k \)が奇数解をもてば, \( k \)は\( 8 \)の倍数であることを示せ。
(2) 方程式\( x^2 – y^2 = k \)が奇数解をもつための必要十分条件を求めよ。
発想
(1)は普通にやるだけ。奇数解をもつのでそれを代入すると, 何か見えてくるはず。
(2)は, もちろん(1)の利用を考える。(1)より奇数解をもつならば\( k \)は\( 8 \)の倍数である。では逆に, \( k \)が\( 8 \)の倍数であれば, 奇数解をもつと言えるだろうか?もし言えたら, これが必要十分条件である。もし言えなければ大変だが, とにかくまずは「\( k \)が\( 8 \)の倍数のとき」から考えてみる。
下書き
(1)
奇数解を\( (x, y) = (2m + 1, 2n + 1) \)(\( m, n \)は整数)とおいて, 方程式\( x^2 – y^2 = k \)に代入してみる。
$$\begin{eqnarray}
k &=& x^2 – y^2 = (x+y)(x-y) \\
&=& (2m+2n+2)(2m-2n) \\
&=& 4(m+n+1)(m-n)
\end{eqnarray}$$
\( k \)が\( 8 \)の倍数であることを言いたいので, あとは\( (m+n+1)(m-n) \)が\( 2 \)の倍数(偶数)であることを言えれば良い。\( 2 \)の倍数の話なので, 偶奇に着目する。
つまり, \( m+n+1 \)と\( m-n \)を足すと, \( (m+n+1) + (m-n) = 2m+1 \)と奇数になるので, \( m+n+1 \)と\( m-n \)の偶奇は異なる。よって, どちらか一方は\( 2 \)の倍数となる。これで証明完了。
このように\( 2 \)式を足し算(または引き算)して偶奇の一致を調べるのが定石であるが, わかりにくければ, 以下のように\( m \)と\( n \)の偶奇を\( 4 \)パターン全て調べてもよい。
| \( m \) | \( n \) | \( m+n+1 \) | \( m-n \) |
| 偶 | 偶 | 奇 | 偶 |
| 偶 | 奇 | 偶 | 奇 |
| 奇 | 偶 | 偶 | 奇 |
| 奇 | 奇 | 奇 | 偶 |
確かに\( m+n+1 \)か\( m-n \)のどちらかは偶数となっている。
(2)
ここまでの構造を確認しておくと, 以下のようになる。
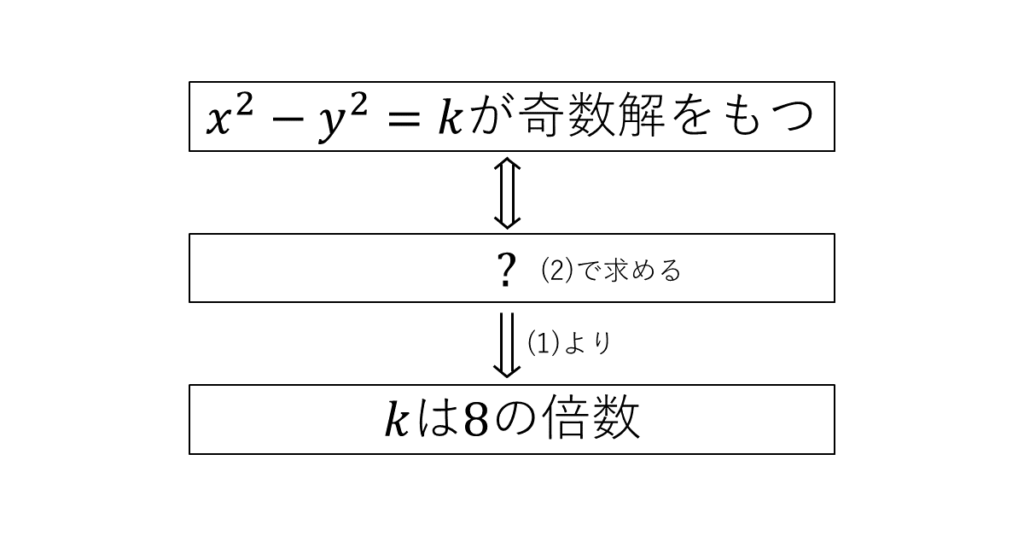
よって, 「\( k \)は\( 8 \)の倍数」より強い条件があるかもしれないが, まずは「\( k \)は\( 8 \)の倍数」から始めてみる。
\( k \)が\( 8 \)の倍数のとき, \( k = 8l \)(\( l \)は\( 0 \)以上の整数)とおける。このとき方程式は, \( x^2 – y^2 = 8l \)となり, これが奇数解をもつかどうかを調べる。
具体的に\( l = 1, 2, 3 \)くらいで, 方程式を満たす\( x, y \)を探してみる。
・\( l = 1 \)つまり\( x^2 – y^2 = 8 \)のとき, \( (x, y) = (3, 1) \)がすぐに見つかる。
・\( l = 2 \)つまり\( x^2 – y^2 = 16 \)のときも, 少し探せば, \( 3:4:5 \)の直角三角形などを思い浮かべながら, \( (x, y) = (5, 3) \)が見つかる。
・\( l = 3 \)つまり\( x^2 – y^2 = 24\)のときは, 頑張って探すと, \( (x, y) = (7,5) \)が見つかる。
なんとなく規則がわかってきたであろうか。表にまとめると以下のようになる。
| \( l \) | \( 8l \) | \( x^2 – y^2 \) |
| \( 1 \) | \( 8 \) | \( 3^2 – 1^2 \) |
| \( 2 \) | \( 16 \) | \( 5^2 – 3^2 \) |
| \( 3 \) | \( 32 \) | \( 7^2 – 5^2 \) |
| \( \cdots \) | \( \cdots \) | \( \cdots \) |
| \( l \) | \( 8l \) | \( (2l+1)^2 – (2l-1)^2 \) |
| \( \cdots \) | \( \cdots \) | \( \cdots \) |
\( l=1,2,3,\cdots \)のときに, \( x \)は\( 3, 5, 7, \cdots \), \( y \)は\( 1, 3, 5, \cdots \)と順に増えているので, 文字\( l \)を使って, \( (x, y) = (2l+1, 2l-1) \)のときに, 方程式を満たしそうである。
実際計算してみると, \( x^2 – y^2 = (2l+1)^2 – (2l-1)^2 = 8l \)となり, 確かに方程式\( x^2 – y^2 = 8l \)を満たしている。
このことから, 「\( k \)は\( 8 \)の倍数」であれば必ず奇数解をもつことが言えるので, (1)と合わせてこれが必要十分条件である。
解答例
(1)
奇数解を持つとき, その奇数解を\( (x, y) = (2m + 1, 2n + 1) \)(\( m, n \)は整数)とおく。
このとき, \( k = x^2 – y^2 = 4(m+n+1)(m-n) \)
ここで, \( m+n+1 \), \( m-n \)はともに整数であり, \( (m+n+1) + (m-n) = 2m+1 \)(奇数)より, \( m+n+1 \)と\( m-n \)の一方は必ず偶数であるから, \( 4(m+n+1)(m-n) \)は\( 8 \)の倍数である。
よって, \( k \)は\( 8 \)の倍数である。
(2)
\( k \)が\( 8 \)の倍数であるとき, \( 0 \)以上の整数\( l \)を用いて, \( k = 8l \)とおける。
このとき, \( x = 2l+1 \), \( y = 2l-1 \)とすると, \( x^2 – y^2 = (2l+1)^2 – (2l-1)^2 = 8l \)より, \( (x, y) = (2l+1, 2l-1) \)は, 方程式\( x^2 – y^2 = 8l \)の解である。
また, \( l \)は整数だから, \( x,y \)はどちらも奇数である。
よって, \( k \)が\( 8 \)の倍数であるとき方程式は奇数解をもつので, (1)と合わせて, 必要十分条件は, \( k \)が\( 8 \)の倍数, である。
振り返り
誘導が付いているのでわかりやすいが, やっていることは, 必要条件から攻める, ということである。奇数解をもつならば, 少なくともこうでなければならない, というものをまず求めておき, 逆にそのとき, 奇数解をもつことを確かめる, というよくあるロジックである。
京大では必要十分条件を求める(示す)問題が頻出であるため、誘導がなくてもこのように求められるようにしておかねばならない。必要十分条件に関してよく理解しておくこと。

コメント