問題
\( N \)を\( 2 \)以上の自然数とし, \( a_n (n = 1, 2, \cdots) \)を次の性質(i), (ii)をみたす数列とする。
(i) \( a_1 = 2^N – 3 \)
(ii) \( n = 1, 2, \cdots \)に対して, \( a_n \)が偶数のとき\( a_{n+1} = \frac{a_n}{2} \), \( a_n \)が奇数のとき\( a_{n+1} = \frac{a_n – 1}{2} \).
このときどのような自然数\( M \)に対しても, \( \displaystyle \sum_{n=1}^M a_n \leqq 2^{N+1} – N – 5 \)が成り立つことを示せ。
下書き
状況把握が大変。実は自然数\( M \)は見掛け倒しで, \( N \)を色々変えて実験してみないといけない。
| \( N \) | \( 2^{N+1} – N – 5 \) | \(a_1\) | \(a_2\) | \(a_3\) | \(a_4\) | \(a_5\) | \(a_6\) | \( a_1 + a_2 + \cdots \) |
| \( 2 \) | \( 1 \) | \( 1 \) | \( 0 \) | \( 0 \) | \( 0 \) | \( 0 \) | \( 0 \) | \( 1 \) |
| \( 3 \) | \( 8 \) | \( 5 \) | \( 2 \) | \( 1 \) | \( 0 \) | \( 0 \) | \( 0 \) | \( 8 \) |
| \( 4 \) | \( 23 \) | \( 13 \) | \( 6 \) | \( 3 \) | \( 1 \) | \( 0 \) | \( 0 \) | \( 23 \) |
| \( 5 \) | \( 54 \) | \( 29 \) | \( 14 \) | \( 7 \) | \( 3 \) | \( 1 \) | \( 0 \) | \( 54 \) |
上の実験から,
・\( a_n \)は単調減少し, 一度\( 0 \)になるとずっと\( 0 \)であること
・各\( N \)について, \( 2^{N+1} – N – 5 \)と\( a_n \)の和は等しいこと
が予測できる。
これらが証明できれば, どんな自然数\( M \)に対しても, (\( M \)が小さいときはもちろん, \( M \)がどれだけ大きくなっても結局は\( 0 \)を足していくだけなので), \( \displaystyle \sum_{n=1}^M a_n \leqq 2^{N+1} – N – 5 \)と言える。
では, \( N \)についての数学的帰納法で, \( 2^{N+1} – N – 5 = a_1 + a_2 + \cdots \)が言えるだろうか?これは, やろうとしてみると, なかなか出来ないことが分かる。
では, 一気に証明するのはあきらめて, まずは\( a_n \)を順に求めてみよう。
・\( a_1 = 2^N – 3 \)
・\( a_2 = \frac{2^N – 3 – 1}{2} = 2^{N-1} – 2 \)
\( N \)が小さいと指数部分がややこしいので, 一旦\( N \)は十分大きいとして次々求めていくと,
・\( a_3 = \frac{2^{N-1} – 2}{2} = 2^{N-2} – 1 \)
・\( a_4 = \frac{2^{N-2} – 1 -1}{2} = 2^{N-3} – 1 \)
・\( a_5 = \frac{2^{N-3} – 1 -1}{2} = 2^{N-4} – 1 \)
よって, \( a_n = 2^{N-n+1} – 1 \)と予想できる。
さらに上の実験から, \( a_n \)は\( 0 \)になってほしいので, そのときの\( n \)を求めると, \( N-n+1 = 0 \)より\( n = N+1 \)。
つまり, \( a_1 = 2^N-3 \), \( a_2 = 2^{N-1} – 2 \), \( n = 3, 4, \cdots, N \)のとき\(a_n = 2^{N-n+1} – 1 \), \( n \geqq N+1 \)のとき\( a_n = 0 \), と予想できる。
これは帰納法で示せそうだし, \( a_n \)の和も求まりそう。一安心。
帰納法
帰納法で示すべきは, \( n = 3, 4, \cdots, N \)のときだけである。(\( 0 \)になった後も続けるとややこしいので, \( n=N \)までで止めておく。帰納法はこのように, 途中まででも適用できる。)
(i) \( n = 3 \)のとき, 上の計算より成り立つ。
(ii) \( n = k \)のとき, \( a_k = 2^{N-k+1} – 1 \)と仮定して, \( a_{k+1} = 2^{N-k} – 1 \)を示す。
\( k = 3, 4, \cdots, N \)より, \( N-k+1 \geqq 1 \)だから, \( a_k = 2^{N-k+1} – 1 \)は奇数である。
よって, 性質(ii)より\( a_{k+1} = \frac{a_k – 1}{2} = \frac{2^{N-k+1} – 2}{2} = 2^{N-k} – 1 \)と計算できるので, 成り立つ。
(i)(ii)より, \( n = 3, 4, \cdots, N \)のとき, \(a_n = 2^{N-n+1} – 1 \)となる。
ここまで言えたら、\( n \geqq N+1 \)のときに\( a_n = 0 \)となる旨の記述は、特別難しくないだろう。
\( a_n \)の和
等比数列の形なので, 和の公式から容易に求まる。
$$\begin{eqnarray}
a_1 + a_2 + a_3 + a_4 + \cdots + a_N + \cdots
&=& (2^N – 3) + (2^{N-1} – 2) + (2^{N-2} \color{red}{- 1}) + (2^{N-3} \color{red}{- 1}) + \cdots + (2^1 \color{red}{- 1}) + 0 \\
&=& (2^N + 2^{N-1} + \cdots + 2^1) -3 -2 + \color{red}{(-1) \cdot (N-2)} \\
&=& 2 \frac{2^N-1}{2-1} -3 -N \\
&=& 2^{N+1} – N -5
\end{eqnarray}$$
これでほぼOKで, 答案にまとめる際には, 小さい\( N \)については別途記述すればよい。
解答例
\( f(M) = \displaystyle \sum_{n=1}^M a_n \)とおく。
① \( N=2 \)のとき
\( a_1 = 1 \), \( a_2 = 0 \)。\( n \geqq 3 \)のときは, 性質(ii)より帰納的に\( a_n = 0 \)。
よって\( f(M) \)の最大値は\( f(1) = 1 \)であり, 任意の\( M \)に対して, \( \displaystyle \sum_{n=1}^M a_n \leqq f(1) = 1 = 2^{2+1} – 2 – 5 \)が成り立つ。
② \( N \geqq 3 \)のとき
\( a_1 = 2^N – 3 \)は奇数, \( a_2 = 2^{N-1} – 2 \)は偶数, \( a_3 = 2^{N-2} – 1 \)は奇数。
\( k = 3, 4, \cdots, N \)のときに, \( a_k = 2^{N-k+1} – 1 \)と仮定する(これは\( k=3 \)のときに成り立つ)。
このとき, \( a_k \)は奇数だから, 性質(ii)より, \( a_{k+1} = 2^{N-k} – 1 \)となり, \( k+1 \)のときも成り立つ。
よって, 数学的帰納法より, \( a_n = 2^{N-n+1} – 1 \)(\( n = 3, 4, \cdots, N \))
したがって, \( a_N = 2^1 – 1 = 1 \)。
性質(ii)より, \( a_{N+1} = 0 \)。
\( n \geqq N+2 \)のときは, 性質(ii)より帰納的に\( a_n = 0 \)。
よって, \( f(M) \)の最大値は\( f(N) \)である。
ここで, \( f(N) = \) (省略:下書き参照) \( = 2^{N+1} – N -5 \)。
したがって, 任意の\( M \)に対して, \( \displaystyle \sum_{n=1}^M \leqq f(N) = 2^{N+1} – N – 5 \)が成り立つ。
振り返り
「どんな自然数\( M \)についても成り立つ」だから, \( M \)についての数学的帰納法, と安易に飛びついてはいけない。とにかく実験が基本。問題を分解していき, 帰納法が使えるようになるタイミングで使う。
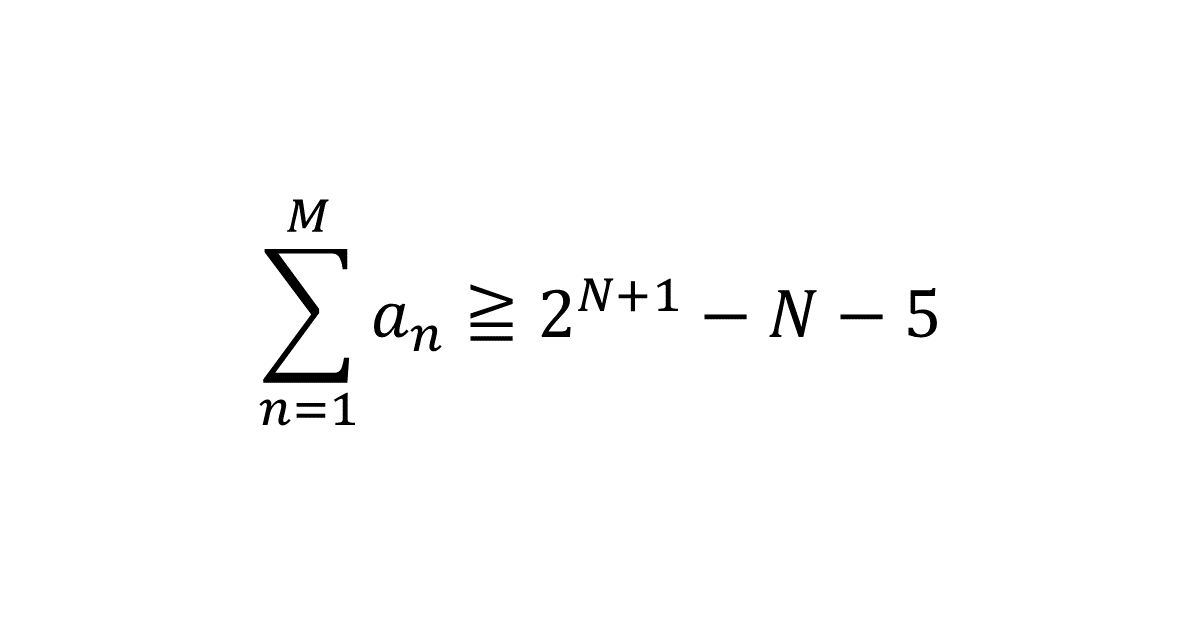
コメント