問題
次の文を読んで, に適した化学反応式, 化学式あるいは数式を, また( )には数値を記入せよ。ただし, (チ)の数値は有効数字2けたで解答せよ。
純水を空気中に放置すると, 空気中の二酸化炭素は吸収され, 溶解する。溶解した二酸化炭素\( \require{mhchem} \ce{CO2(aq)} \)の一部は電離し, 下の(1)式および(2)式に示すように炭酸水素イオンおよび炭酸イオンを生じる。
\begin{align}
&\ce{CO2(aq) + H2O <=> H+ + HCO3-} \cdots (1) \\
&\ce{HCO3- <=> H+ + CO3^2-} \cdots (2)
\end{align}
これに炭酸カルシウムを投入すると, (3)式の反応が起こり, 炭酸カルシウムが溶解する。
イ \( \cdots (3) \)
この溶液を\( 25 {}^\circ \rm{C} \)で大気中に長時間放置したところ, 炭酸カルシウムはすべて溶解し平衡に達した。このとき, 水中に存在する炭素化合物のうち, 大気から吸収された\( \ce{CO2} \)によるものの量を求めてみよう。
水中の二酸化炭素の平衡濃度は\( 25 {}^\circ \rm{C} \)で\( 1.2 \times 10^{-5} \ce{mol / L} \)であり, その電離に関する平衡定数\( K_1, K_2 \)および水のイオン積\( K_W \)は,
\begin{align}
&K_1 = \frac{[\ce{H+}][\ce{HCO3-}]}{\ce{[CO2(aq)]}} = 4.4 \times 10^{-7} \ce{mol / L} \cdots (4) \\
&K_2 = \frac{[\ce{H+}][\ce{CO3^2-}]}{[\ce{HCO3^-}]} = 4.7 \times 10^{-11} \ce{mol / L} \cdots (5) \\
&K_W = 1.0 \times 10^{-14} (\ce{mol / L})^2 \cdots (6)
\end{align}
である。さらに, この水溶液は電気的に中性であるため, 陽イオンの総電荷数と陰イオンの総電荷数は等しいことを考慮すると, 溶液中の各種イオンの濃度間には次の関係が成立する。
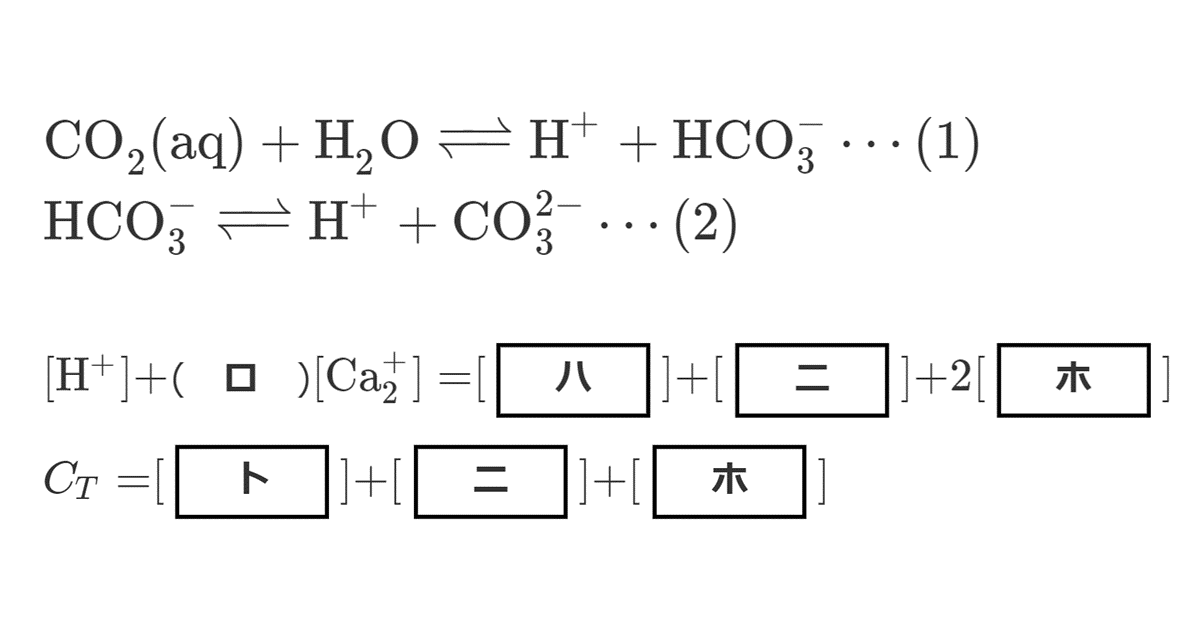
\( \ce{[H+]} + \)( ロ )\( \ce{[Ca^2+]} = [ \)ハ\( ] + [ \)ニ\( ] + 2[ \)ホ\( ] \cdots (7) \)
(4)~(7)式の関係から, 平衡状態におけるカルシウムイオン濃度は, \( K_1 \), \( K_2 \), \( K_W \), \( \ce{[H+]} \)および\( \ce{[CO2(aq)]} \)を用いて, (8)式のように表すことができる。
\( \ce{[Ca^2+]} = \)ヘ\( \cdots (8) \)
さらに, 水中に存在する炭素化合物の全濃度\( C_T \)は,
\( C_T = [ \)ト\( ] + [ \)ニ\( ] + [ \)ホ\( ] \)
により与えられる。
さて, 平衡に達したときの溶液の\( \ce{pH} \)は\( 8.0 \)であった。以上の関係式を用いると, 水中に存在する炭素化合物のうち大気に由来する量は, 水\( 1 \rm{L} \)あたり( チ )\( \ce{mol} \)となる。
解説
イ
炭酸カルシウム, 溶解というキーワードから, \( \ce{Ca(HCO3)2} \)が思い浮かび, \( \ce{CaCO3 -> Ca(HCO3)2} \)まで書ける。これは, 有名な石灰水の再溶解の反応(二酸化炭素を加えると一旦沈殿し, さらに加えると再び透明になる)でよく出てくるので, 左辺に\( \ce{CO2} \)を加えて適当に数を合わせる。
\( \ce{Ca} \)系はややこしいので, 以下に簡単にまとめておく。
まず, 天然に広く存在する石が\( \underline{\ce{CaCO3}} \)で, それを燃やすと石の灰みたいなものが出来る。これは加工しやすく様々な用途に使えるので, 生石灰(\( \ce{CaO} \))と呼ぶ。これを放置すると大気中の水と反応して, 加工性を失う。これを消石灰(\( \ce{Ca(OH)2} \))と呼ぶ。これらの石灰のもとになる石ということで, \( \underline{\ce{CaCO3}} \)を石灰石と呼ぶ。
石灰(生でも消でも可)の水溶液が, 石灰水である。一般に, 消石灰の水溶液と書かれることが多いが, 上記の通り生石灰の水溶液は即座に消石灰の水溶液になるので, あまり区別する必要はない。
石灰水に二酸化炭素を通じると, 以下の2式によって沈殿および再溶解する(後者が本問の答え)。
\begin{align}
&\ce{Ca(OH)2 + CO2 -> CaCO3 + H2O} \\
&\ce{CaCO3 + CO2 + H2O -> Ca(HCO3)2}
\end{align}
ロ~ホ
電離平衡の問題では, 電気的つり合いの式が重要である。
例えば, 体積\( V \)中に\( \ce{A+} \)イオンと\( \rm{B}^{\color{red}{2}-} \)イオンが存在し, 水溶液自体は中性であるとき, プラスの電荷は\( [\ce{A+}] \times V [\ce{mol}] \), マイナスの電荷は\( [\ce{B^2-}] \times V \times \color{red}{2} [\ce{mol}] \)存在する。よって, \( [\ce{A+}] = \color{red}{2} [\ce{B^2-}] \)が成り立つ。
水中の全てのイオン(\( \ce{H+} \), \( \ce{OH-} \), \( \ce{Ca^2+} \), \( \ce{HCO3-} \), \( \ce{CO3^2-} \))について, 価数を考慮して釣り合いの式を立てる。なお, ハとニは, この式だけ見ると対称であるが, 後ろの問題文にニが出てくるので, 対称ではないことに注意。
ヘ
変数が多いので, 見通しを立てて式変形をしていく。\( [\ce{Ca^2+}] \)は\( [\ce{H+}] + 2[\ce{Ca^2+}] = [\ce{OH-}] + [\ce{HCO3-}] + 2[\ce{CO3^2-}] \)(7)式でしか使われていないので, \( [\ce{H+}] + 2[\ce{Ca^2+}] = [\ce{OH-}] + [\ce{HCO3-}] + 2[\ce{CO3^2-}] \)(7)式をもとにして考える。
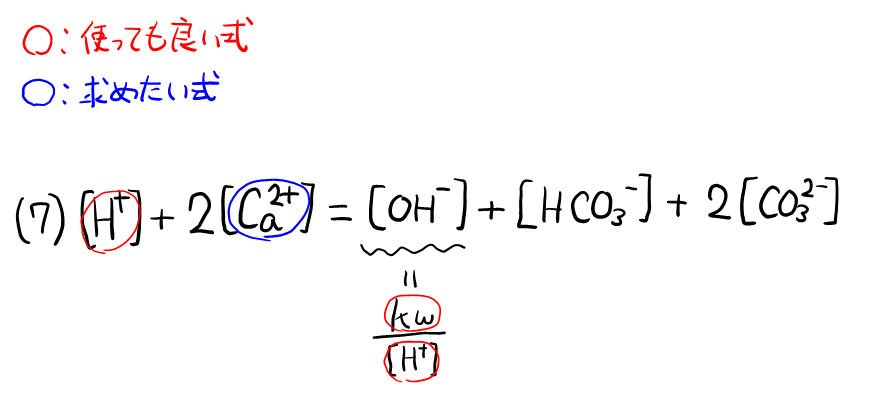
まず, 左辺の\( [\ce{H+}] \)は使って良いと言われているのでそのまま。\( [\ce{OH-}] \)も水のイオン積を使って\( [\ce{H+}] \)で表せるので問題ない。
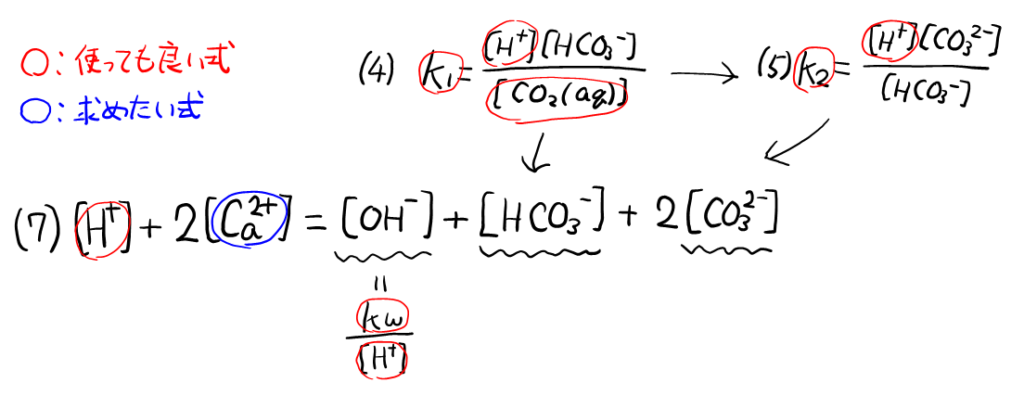
次に\( [\ce{HCO3-}] \)は, \( K_1 = \frac{[\ce{H+}][\ce{HCO3-}]}{\ce{[CO2(aq)]}} \)(4)式と\( K_2 = \frac{[\ce{H+}][\ce{CO3^2-}]}{[\ce{HCO3^-}]} \)(5)式に出てくるが, \( K_2 = \frac{[\ce{H+}][\ce{CO3^2-}]}{[\ce{HCO3^-}]} \)(5)式には使えない\( [\ce{CO3^2-}] \)も入っているので\( K_1 = \frac{[\ce{H+}][\ce{HCO3-}]}{\ce{[CO2(aq)]}} \)(4)式を見てみると, \( [\ce{HCO3-}] \)以外はすべて使って良い式になっている。
最後に\( [\ce{HCO3^2-}] \)は, \( K_2 = \frac{[\ce{H+}][\ce{CO3^2-}]}{[\ce{HCO3^-}]} \)(5)式と, 先ほど出した\( [\ce{HCO3-}] \)を使えば, 使って良い文字だけで表せる。
ト(, 二, ホ)
電気的つり合いの式のほかに, 原子数のつり合いの式もよく出題される。
例えば, 体積\( V [\ce{L}] \)中に\( \ce{CA} \)と\( \ce{C2B} \)が存在するとき, \( \ce{C} \)原子は\( [\ce{CA}] \times V + [\rm{C_{\color{red}{2}}B}] \times \color{red}{2} \times V [\ce{mol}] \)存在する。よって, \( \ce{C} \)原子の濃度は, \( [\ce{CA}] + \color{red}{2}[\rm{C_{\color{red}{2}}B}] [\ce{mol / L}] \)である。このように, 体積\( V \)は消えるので, 濃度を足し算するようなことができる, ということがポイントである。
本問では, 出てくる化学式の\( \ce{C} \)原子の係数はすべて1なので, 単純にすべての濃度を足せばよい。
チ
改めて本問の実験をまとめる。純水を放置して空気中の二酸化炭素を溶かし, そこに炭酸カルシウムを加える。長時間経過後の炭素化合物のうち, 空気由来の\( \ce{C} \)濃度を求める。
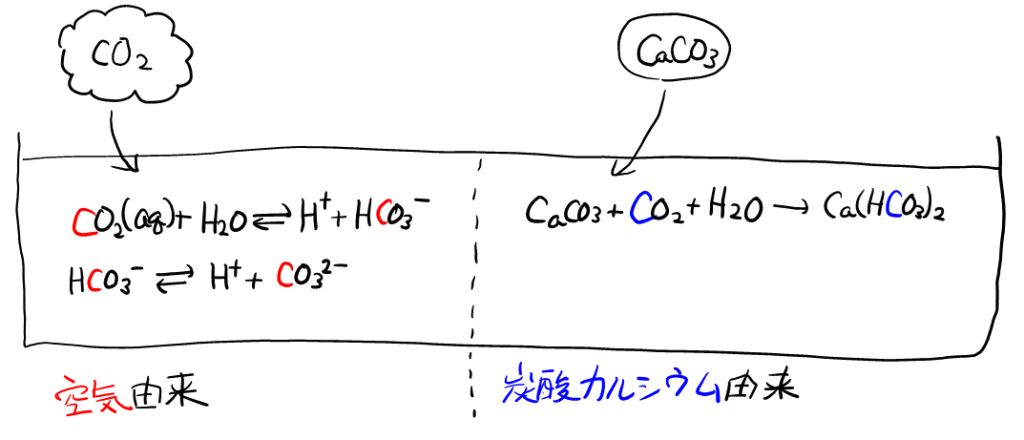
ここで, 右側の式は, \( \rm{\color{blue}{C}O_2} \)や\( \rm{H\color{blue}{C}O_3^-} \)があり, 炭酸カルシウム由来か空気由来かを考えるこの問題では, 左側の2式の中の\( \rm{\color{red}{C}O_2} \)や\( \rm{H\color{red}{C}O_3^-} \)と混同しやすい。\( \ce{CaCO3} \)の溶解を, 思い切って書き換えてみる。炭酸カルシウムは難溶性塩だが, すべて溶解したと書いてあるので, 以下のように書ける。
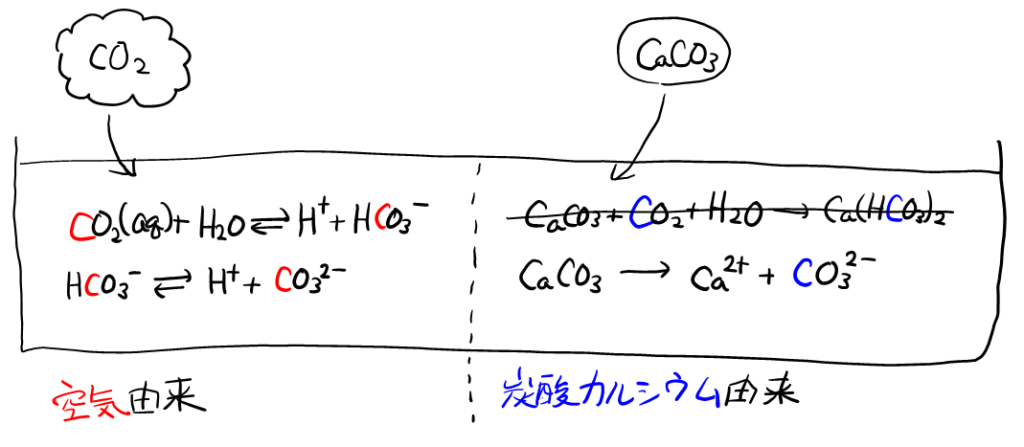
これで, 水中に残った炭素化合物は, 空気由来の\( \rm{\color{red}{C}O_2} \), \( \rm{H\color{red}{C}O_3^-} \), \( \rm{\color{red}{C}O_3^{2-}} \), 炭酸カルシウム由来の\( \rm{\color{blue}{C}O_3^{2-}} \), のみになった。
求めるのは空気由来の炭素だが, 明らかに数が少ない炭酸カルシウム由来の\( \rm{\color{blue}{C}O_3^{2-}} \)を求める方が簡単である。それがわかれば, \( C_T = [\rm{\color{red}{C}O_2}] + [\rm{H\color{red}{C}O_3^-}] + [\rm{\color{red}{C}O_3^{2-}}] + [\rm{\color{blue}{C}O_3^{2-}}] \)\( C_T \)の式から, 引き算で求められる。
ここで, 書き換えた式\( \ce{CaCO3 -> Ca^2+ +} \rm{\color{blue}{C}O_3^{2-}} \)より\( [\rm{\color{blue}{C}O_3^{2-}}] = [\ce{Ca^2+}] \)だから, \( [\ce{Ca^2+}] = (K_1, K_2, K_W, [\ce{H+}], [\ce{CO2(aq)}]だけの式) \)(8)式より\( [\rm{\color{blue}{C}O_3^{2-}}] \)が求められる。
振り返り
電気的つり合いの式と, 原子数のつり合いの式は, 多くの状況で成り立つ式であるので, すぐに立式できるようにしておくことが大切。
最後の( チ )は, 考え方もその後の計算もかなり難しいので, 本番では他の問題の見直しに時間を使うべきである。余裕がある人は考え方だけ確認しておこう。
このような問題では, 意外とイのような反応式の問題で差が付きやすいので, 間違えた人は注意が必要。
コメント