問題
次の文を読んで, 問1~問5に答えよ。ただし, 数値は有効数字2けたで解答せよ。気体はすべて理想気体とみなし, 気体定数\( R \)は\( 0.082 \rm{L \cdot atm / (K \cdot mol)} \)である。
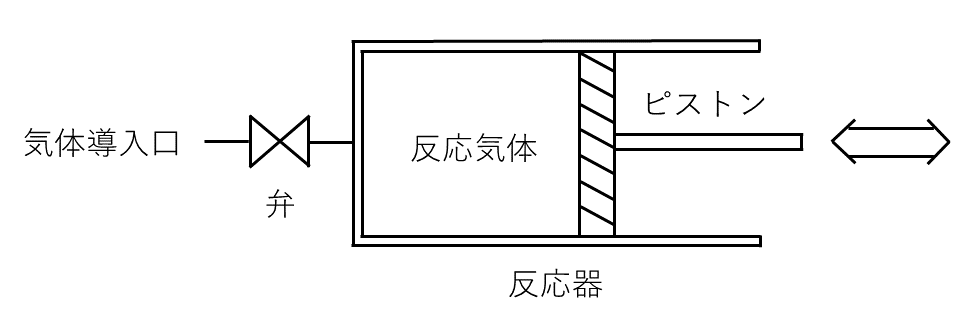
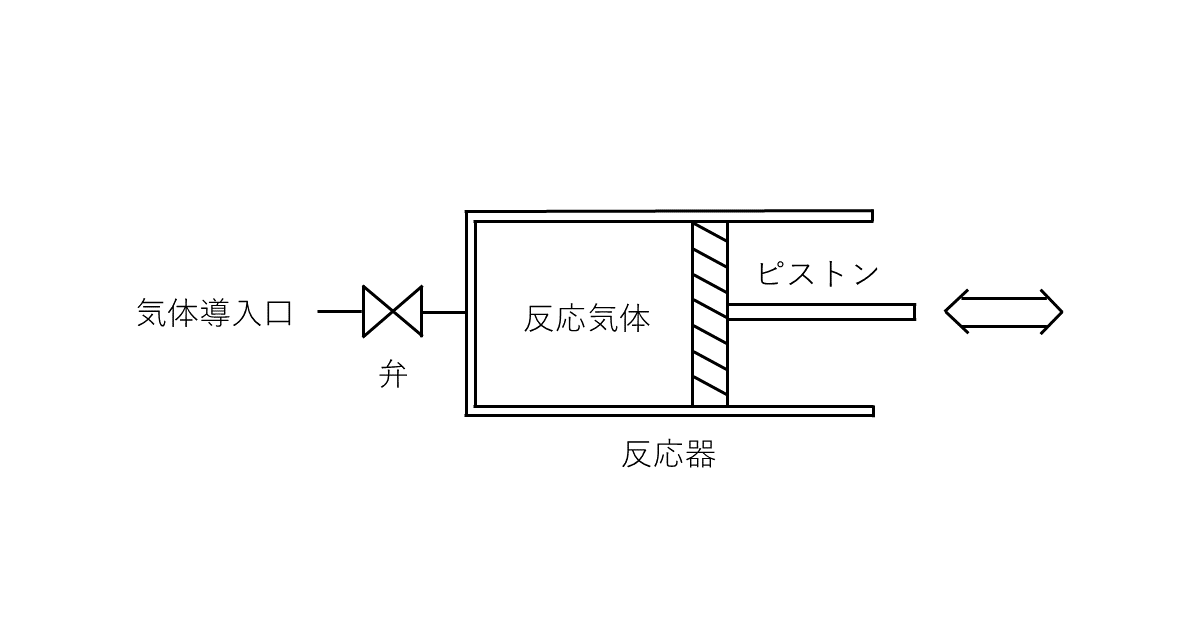
式(1)で表される気体\( \rm{A} \)と気体\( \rm{B} \)の間の可逆反応を, 図に示す反応器を用いて行わせる。
$$ \require{mhchem} \ce{A <->} b \ce{B} \tag{1} $$
ただし, \( b \)は\( \rm{B} \)の係数である。この反応器の容積は, ピストンを用いて自由に変えることができる。いま, 反応器に気体\( \rm{A} \)をいれ, 温度を速やかに\( 500 {}^\circ \rm{C} \)に上昇させたところ, 反応開始時の反応器の容積は\( 1.00 \rm{L} \), 圧力は\( 1.00 \rm{atm} \)であった。その後, 反応がゆるやかに進行するにつれ, ピストンを移動させて, 反応器内を\( 500 {}^\circ \rm{C} \), \( 1.00 \rm{atm} \)に保った。平衡状態になったとき, 反応器の容積は\( 1.64 \rm{L} \), 気体\( \rm{B} \)のモル濃度は\( 0.0123 \rm{mol / L} \)であった。
反応式(1)の係数\( b \)の値を求めてみる。反応器に入れた\( \rm{A} \)の量を\( n \rm{mol} \), 反応した\( \rm{A} \)の量を\( x \rm{mol} \)とする。反応開始時に\( 1.00 \rm{L} \)あった容積が, この反応が平衡に達したときに\( 1.64 \rm{L} \)になることから, 次の関係が成立する。
イ\( : \)ロ\( = 1.00 : 1.64 \)
この関係と平衡状態での\( \rm{B} \)のモル濃度とから\( n= \)ハ, \( x= \)ニ, \( b= \)ホとなる。
問1 文中のイ, ロには\( b, n \)と\( x \)などを用いた適切な式を, ハ~ホには適切な数値を記入せよ。
問2 次に示す(あ)から(く)の気体の反応のうちで, 温度と圧力を一定に保って, 左辺の気体を右辺の気体に変化させたとき, \( b \)がホの値をとるものとして, 体積変化の割合が反応式(1)と同じになるものをすべて選べ。解答は記号で答えよ。
| (あ) \( \ce{2HCl <-> H2 + Cl2} \) | (い) \( \ce{CH3OH <-> CO + 2H2} \) |
| (う) \( \ce{2NH3 <-> N2 + 3H2} \) | (え) \( \ce{2SO3 <-> 2SO2 + O2} \) |
| (お) \( \ce{2CH4 <-> C2H4 + 2H2} \) | (か) \( \ce{2C2H4 <-> C4H8} \) |
| (き) \( \ce{C6H12 <-> C6H6 + 3H2} \) | (く) \( \ce{C2H5OH <-> C2H4 + H2O} \) |
問3 気体\( \rm{A} \)と\( \rm{B} \)のモル濃度(\( \rm{mol / L} \))をそれぞれ\( [\rm{A}] \)と\( [\rm{B}] \)で表すとき, 圧力\( 1.00 \rm{atm} \), 温度\( 500 {}^\circ \rm{C} \)における式(1)の反応の平衡定数\( K \)を求めよ。ただし, \( K \)は次式で定義される。
$$ K = \frac{{[\rm{B}]}^b}{[\rm{A}]} \tag{2} $$
問4 式(2)の平衡定数\( K \)は, 圧力\( 1.00 \rm{atm} \), 温度\( 300 {}^\circ \rm{C} \)では\( 500 {}^\circ \rm{C} \)の場合の約\( 1/3 \)になった。式(1)の反応が左から右へ進むとき, 次の(a)と(b)のうち正しいものを選び, 記号で答えよ。
| (a) この反応は発熱反応である | (b) この反応は吸熱反応である |
問5 式(1)の反応を, ある温度と圧力のもとで行わせたところ, 平衡に達したときの容積が\( 1 \rm{L} \)であった。その後, 温度を一定に保ちながら, ピストンを移動して, 容積を\( 0.2 \rm{L} \)にすると, 平衡はどうなるか。次の(a)から(c)のうち正しいものを選び, 記号で答えよ。
| (a) 左に移動する | (b) 右に移動する | (c) 変わらない |
解説
問1
イ, ロ
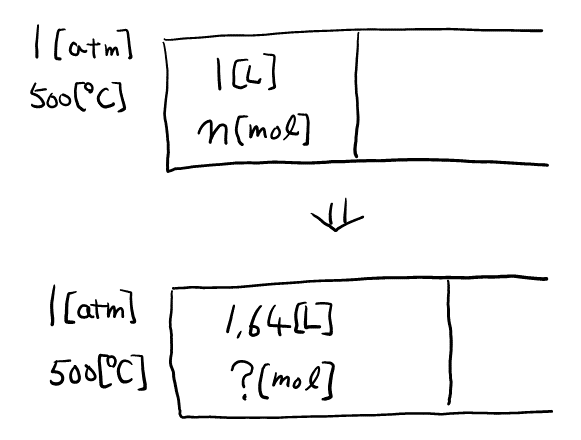
反応開始時の情報と平衡時の情報を見比べて, \( T \)と\( P \)が一定であることがわかる。ここから, 状態方程式\( PV = nRT \)より, \( V \)と\( n \)が比例関係であることをまず押さえておく。
反応の表を書くと, 以下のようになり, 平衡時の\( \rm{mol} \)がわかる。
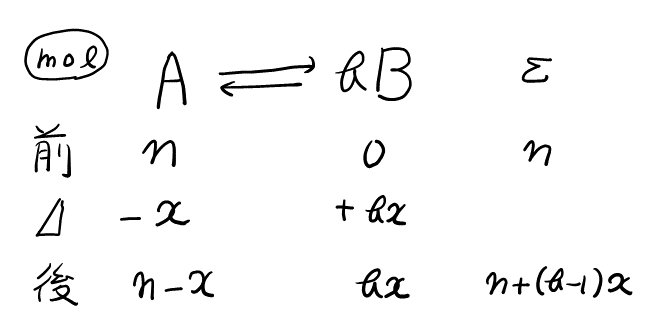
よって, \( V \)と\( n \)が比例関係より, \( V \)が増えると同じ割合だけ\( n \)も増えるので, \( 1.00:1.64 = n:n+(b-1)x \)。
ハ~ホ
3変数なので, 式を3つ探す。1つ目は, イとロで求めた比例式。2つ目は, 図より状態方程式で\( n \)が求まりそう。3つ目は, 「平衡状態になったとき, …, 気体\( \rm{B} \)のモル濃度は\( \underline{0.0123 \rm{mol / L}} \)であった」という条件をまだ使っていないので, そこから導けそう。
1つ目の式を整理すると, \( 0.64n = (b-1)x \)…①
2つ目の式は, 状態方程式から\( n \)を求めるだけで, \( n = \frac{1.00 \times 1.00}{0.082 \times 773} = 0.0157 \)…②
3つ目の式について, 平衡時の\( \rm{B} \)の\( \rm{mol} \)は\( bx[\rm{mol}] \), 体積は\( 1.64 [\rm{L}] \)だから, \( 0.0123 = \frac{bx}{1.64} \)…③
①と③を見比べると, \( b \)や\( x \)を消去するより, \( bx \)をまとめて①に代入すると, 計算が少し楽になるかもしれない(①を変形すると, \( x = bx – 0.64n \)となり, \( bx \)と\( n \)から\( x \)が求まる)。
いずれにせよただの計算問題なので, 5~10分程度で答えを出してしまおう。その際, \( b \)は係数なので, (簡単な分数になる可能性もゼロではないが)整数になるだろうと予測して, 計算を進めると良い。
問2
何を聞いているかわかりにくいかもしれない。既に見たように, 温度と圧力が一定であれば, 体積変化の割合は物質量変化の割合と一致する。よって, 反応式の左右の係数の比を見て, \( 1:2 \)で反応しているものを選べばよい。
問3
簡単なので省略。
問4
平衡定数が小さくなったということは, 式(2)より, \( [\rm{A}] \)が増えて\( [\rm{B}] \)が減った, つまり, 反応が左に進んだことがわかる。
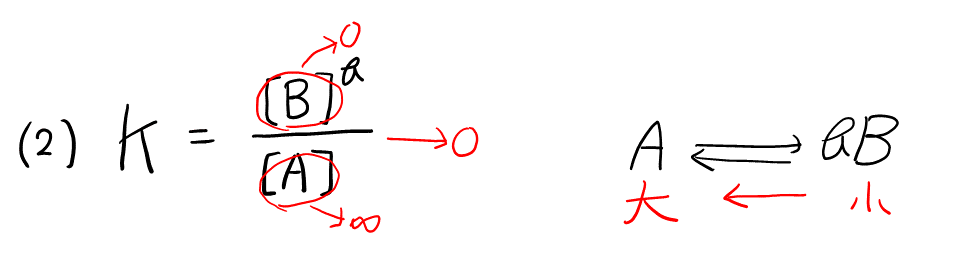
ここで, 発熱反応だと仮定すると, 温度を下げたときに, 温度を上げる方向へ進んでしまう。よって, 吸熱反応だと判断できる。
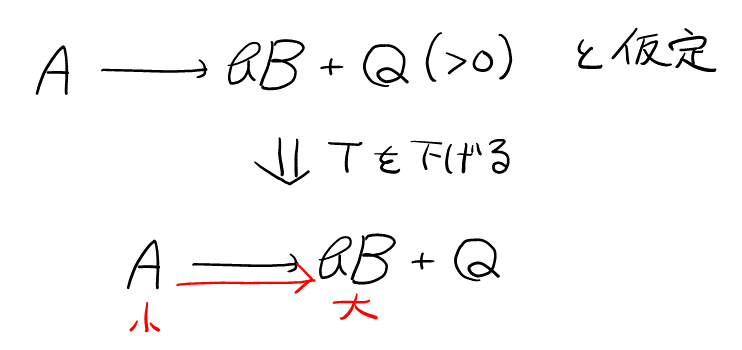
このように, 化学では表裏一体の関係(陽と陰, 正と負など)が多いので, 一方だと仮定して矛盾が無ければOK, 矛盾が生じれば他方, と判断すると早いことが多い。
問5
今度は温度だけ一定なので, 容積を小さくすると圧力は大きくなる(イメージできない人は\( PV = nRT \)を思い浮かべること)。よって, 変化を和らげる, 圧力を小さくする方向へ進むので, 反応式の(気体の)係数を見て, 係数が大→小の方向へ進む。
振り返り
非常に基礎的な内容。問4や問5も解説を書いたが, 本来は解説が要らないくらい簡単。問1レベルの計算で間違わないことと, 問2で聞かれていることを正しく把握することが求められている。
コメント