問題
次の文を読んで, 問1~問5に答えよ。解答はそれぞれ所定の解答欄に記入せよ。
窒素(\( \require{mhchem} \ce{N2} \))と水素(\( \ce{H2} \))からアンモニアを合成する反応は次式で与えられる。
\( \ce{N2(気) + 3H2(気) = 2NH3(気) + 92kJ} \) (1)
アンモニアは式(1)の逆反応で\( \ce{N2} \)と\( \ce{H2} \)に分解する。いま, \( \ce{N2} \)と\( \ce{H2} \)の物質量比(モル量比)が\( 1 : 3 \)の混合気体を, 温度\( 500 {}^\circ \rm{C} \), 圧力\( 600 \)気圧で, 触媒の存在のもとに長時間保つと, ①混合気体は平衡に達する。平衡状態では体積百分率で全体の40%がアンモニアである。式(1)の反応はア熱反応であるので, 温度を高くすると平衡状態でのアンモニアの割合はイする。アンモニア分子では窒素原子のa個の価電子のうち, b個は結合に関与しないウを形成する。このため, アンモニアは\( \ce{H+} \)とエ結合を作って\( \ce{NH4+} \)となる。
アンモニアは水に溶解すると, その一部は水分子と反応して次の平衡が成り立つ。
\( \ce{NH3 + H2O <->} \)1\( + \)2 (2)
このため, アンモニア水はオ性を示す。いま, ②温度\( 25 {}^\circ \rm{C} \)で\( n_1 \rm{mol} \)のアンモニアと\( n_2 \rm{mol} \)の塩化アンモニウムを加えて得られる全体で\( 1 l \)の水溶液の\( \rm{pH} \)を考えよう。アンモニアの電離定数を\( K \)とすると,
\( K = \)3\( = 1.7 \times 10^{-5} (\rm{mol}/l) \) (3)
と表される。水のイオン積を\( K_W \)とすると,
\( K_W = [\ce{H+}][\ce{OH-}] = 1.0 \times 10^{-14} (\rm{mol}/l)^2 \) (4)
である。また, 水溶液全体では電荷はゼロでなければならないので,
4\( = [\ce{Cl-}] = n_2 (\rm{mol}/l) \) (5)
が成り立つ。さらに, 窒素原子はアンモニアまたはアンモニウムイオンの形で存在するので,
5\( = n_1 + n_2 (\rm{mol}/l) \) (6)
である。濃度に対する連立方程式(3)~(6)をすべての濃度が正であるという条件のもとで解けば, 水素イオン濃度および\( \rm{pH} \)が正確に求められる。しかし, 実際は多くの場合, ある化学種の濃度が他の化学種の濃度よりもはるかに小さいとして, 計算を簡略化することができる。
また, 式(2)の平衡において, 右向きの反応速度は\( k_1[\ce{NH3}][\ce{H2O}] \)で, 左向きの反応速度は\( k_2[ \)1\( ][ \)2\( ] \)で与えられるとすれば, \( k_1 \), \( k_2 \)および\( K \)の間には,
\( K = \)6 (7)
の関係がある。
問1 a, bに適切な数を入れよ。
問2 ア~オに適切な語を入れよ。
問3 1, 2には適切な化学式を, 3~5には適切な式を入れよ。
問4 下線部①の平衡に達したとき, 最初の混合気体の何パーセントが反応したことになるか。有効数字2けたで答えよ。
問5 下線部②において, \( n_1 = 0.010 \rm{mol} \)のとき, ちょうど\( \rm{pH} = 9 \)の溶液を作るには, \( n_2 \)をいくらにしなければならないか。有効数字2けたで答えよ。
解説
問4
問題文を最初から読んでいって, 情報が十分に出揃っていそうな下線部①の問4から片付ける。\( T, P \)一定なので, \( V \)と\( n \)は比例する(\( PV = nRT \)より)ことに注意。よって, 体積百分率はモル百分率と同じなので, 例の表を書いてモルの増減を追う。最初の\( \ce{N2} \)と\( \ce{H2} \)の物質量を\( n \)と\( 3n \), 求める数字(反応した割合)を\( \alpha \)と置くと,
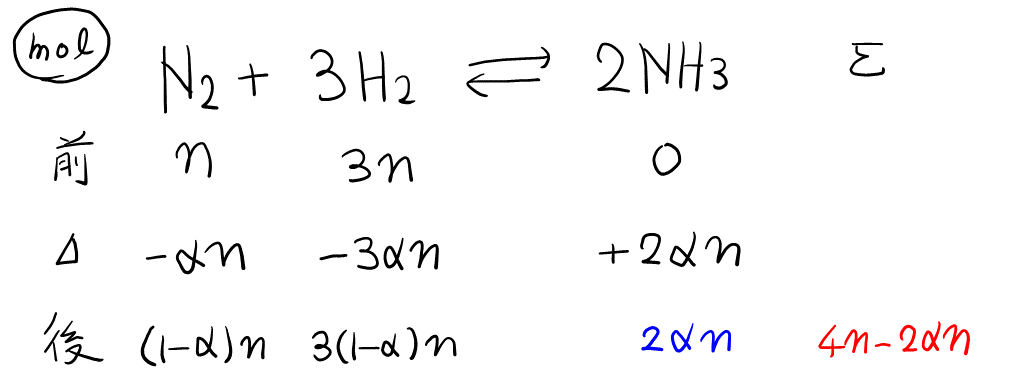
この表から, アンモニアの存在割合(40%)\( = \frac{\color{blue}{2n\alpha}}{\color{red}{4n – 2n\alpha}} \)より\( \alpha \)が求まる。
問1, 問2, 問3(1)(2)
下線部②までの穴埋めは易しいので省略。
問3
(3)
電離定数は, \( [\ce{H2O}] \)を省略する(ほぼ一定とみなせるため)。水の電離定数(水のイオン積)で\( [\ce{H2O}] \)を省略したり, 溶解定数(溶解度積)で固体の濃度を省略するのと同じである。
\( [\ce{H2O}] \)を省略すべきか含めるべきか自信が無くても, この問題の場合は, 単位に注目すれば判断できるようになっている。
なお, 「平衡」定数を聞かれた場合は, 定義に従って省略しない場合もたまにあるが, 今回は「電離」定数を聞かれているので, 自信をもって\( [\ce{H2O}] \)を省略すればよい。
(4)
「電荷はゼロでなければならない」の文言から, 京大化学で頻出の, 電気的つり合いの式。まず, 以下の図を参考にしながら, 水溶液中の全ての化学種を列挙すると, \( \ce{H2O} \), \( \ce{H+} \), \( \ce{OH-} \), \( \ce{NH3} \), \( \ce{NH4+} \), \( \ce{Cl-} \)。ここで, \( \ce{NH4Cl} \)は完全に水に溶けるので残っていないことに注意。
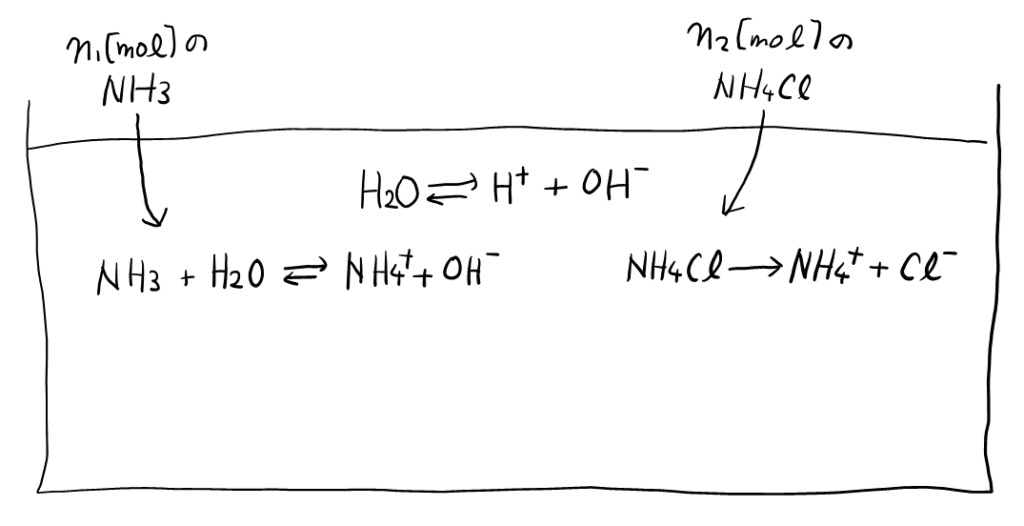
水溶液全体で中性なので, プラスとマイナスの量がつり合っている。つまり, \( [\ce{H+}] + [\ce{NH4+}] = [\ce{OH-}] + [\ce{Cl-}] \)が成り立つ。
(5)
こちらも京大化学で頻出の, 原子数のつり合いの式。ここは難しく考えなくても, 何となく書いて正解した人も多いはず。
念のため, 以下のように表を書けば, 確かに正しいことが確かめられる(変化量\( x \)は自分で置いた)。
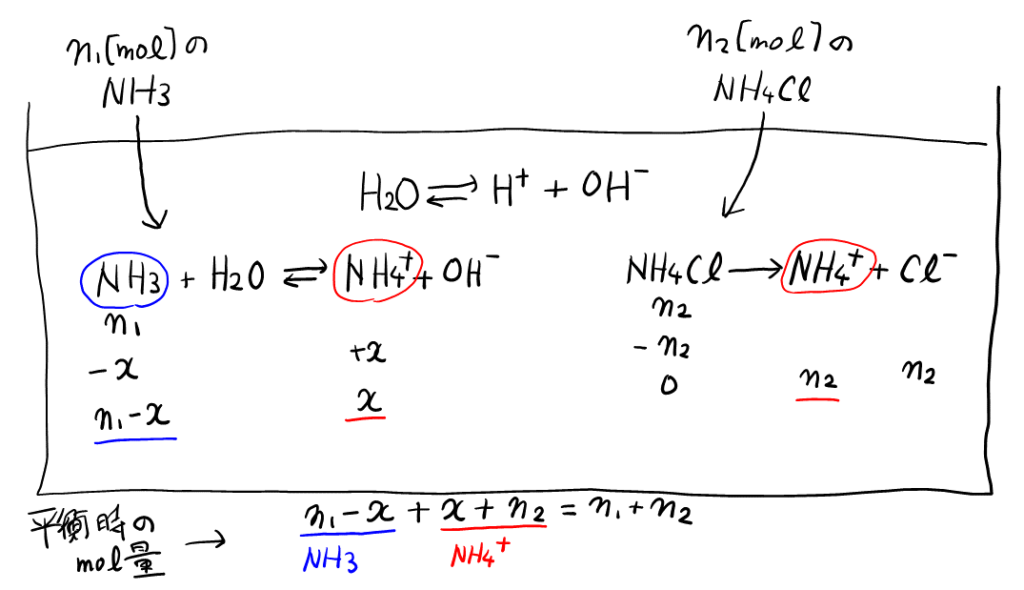
(6)
省略。
問5
問題文より, 簡略化(つまり近似)して連立方程式(3)~(6)を解けばよい。化学の近似では, \( 100 \)倍以上の足し算は無視できることを押さえておこう。つまり, \( 100 \pm 1 \)は\( 100 \)として扱う。
\( n_1 = 0.010 \rm{mol} \), \( \rm{pH} = 9 \)の条件下で式(3)~(6)をまとめると, 以下のようになる。
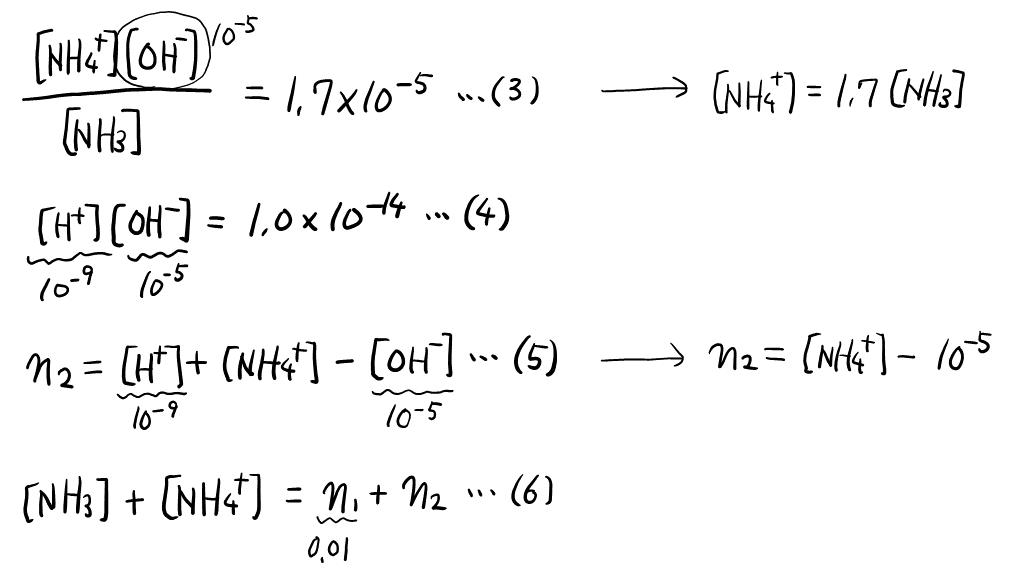
式(5)を見ると, \( 10^{-9} \)と\( 10^{-5} \)は\( 100 \)倍以上違うので, \( 10^{-9} \)の方は無視できる。また, 式(3)からも, \( [\ce{NH4+}] = 1.7[\ce{NH3}] \)というきれいな式が得られる。よって, 式(5)(6)から\( [\ce{NH4+}] \)を消去して, \( [\ce{NH3}] \)と\( n_2 \)の連立方程式に帰着できる。
$$\left\{
\begin{array}{l}
n_2 = 1.7[\ce{NH3}] – 10^{-5} \cdots (5)’ \\
2.7[\ce{NH3}] = 0.01 + n_2 \cdots (6)’ \\
\end{array}
\right.$$
これらの式を見ると, 式(5)’の\( 10^{-5} \)は無視してしまいたくなるかもしれない(実際それは正しい)が, \( [\ce{NH3}] \)が\( 10^{-4} \)くらいの可能性もあるので, 安易に無視はできない。もはやただの連立方程式なので容易に厳密解が求められ, 少し計算すると\( n_2 = 0.017 – 10^{-5} \)となる。ここで, \( 100 \)倍以上の差があるので\( 10^{-5} \)が無視でき, \( n_2 = 0.017 \)が答えとなる。
振り返り
問3(4)(5)のつり合いの式は過去問演習量が問われる問題で, 必ず正解したい。ただし, (5)の方は少し難しい。
問5で差が付く。この種の近似計算に慣れていないと難しいので, 最初は出来なくてもよいが, 小さい数字を無視するだけの単なる計算問題なので, 解説を読んで理解し, 慣れておく必要がある。
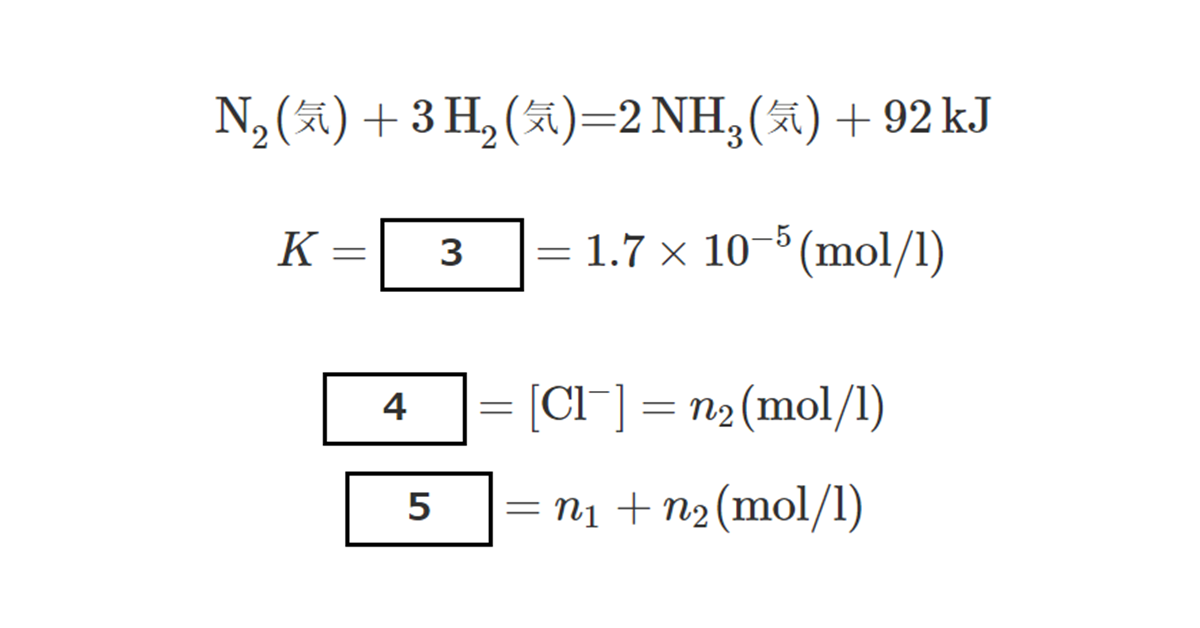
コメント