問題
次の文を読んで, 問1~問3に答えよ。解答はそれぞれ所定の解答欄に記入せよ。ただし, 濃度の単位は\( \require{mhchem} \text{mol} / l \), 体積の単位は\( l \)とする。
ある物質\( \rm{A} \)が次の不可逆反応(1), あるいは可逆反応(2)によって物質\( \rm{B} \)に変化する2種の反応について考える。
\begin{align}
&\ce{A -> B} \cdots (1) \\
&\ce{A <=> B} \cdots (2)
\end{align}
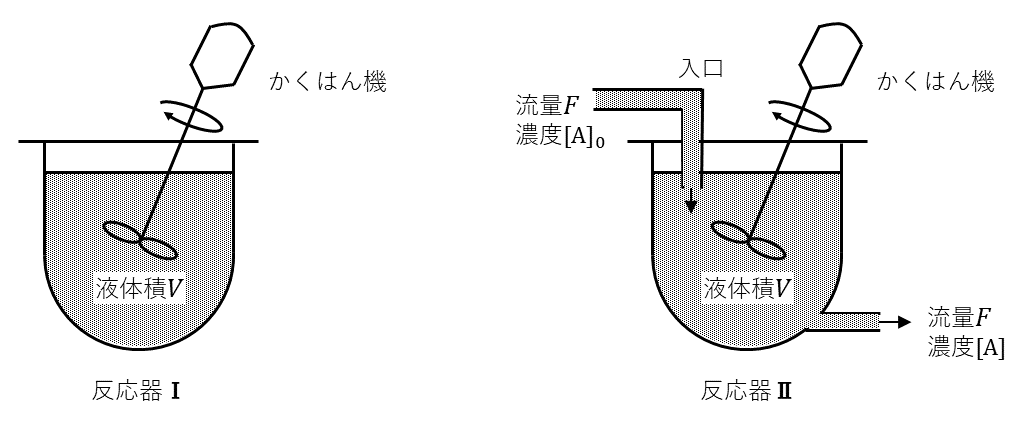
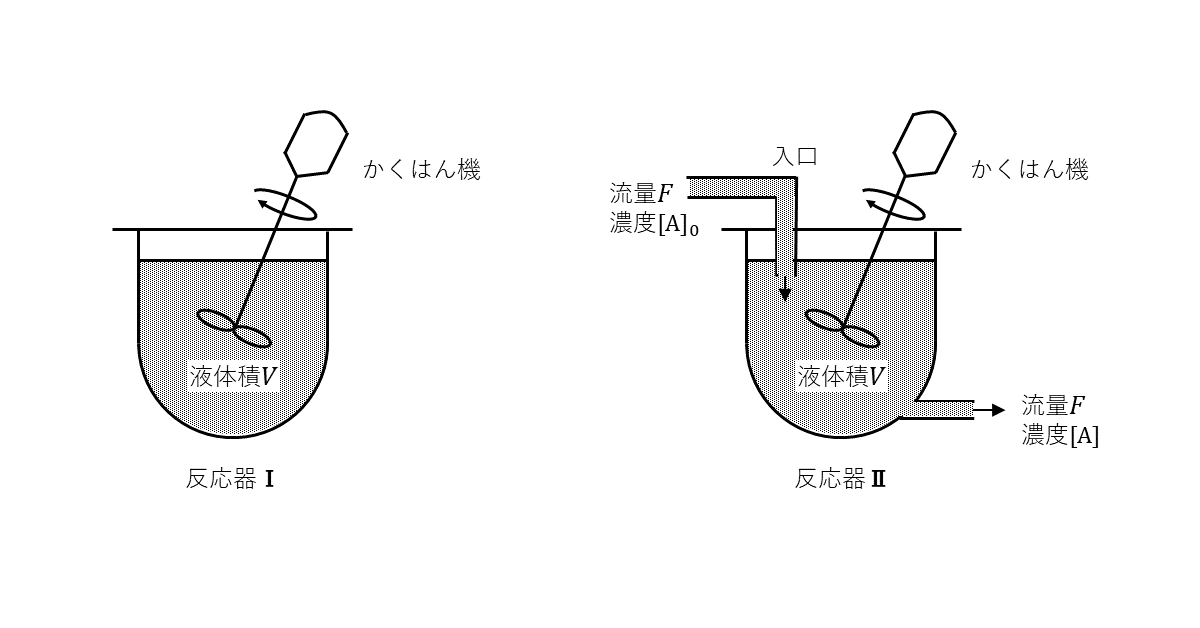
それぞれの反応について, 図1に示した2種類の反応器ⅠとⅡを用いた実験を行った。まず物質\( \rm{A} \)を濃度\( [\rm{A}]_0 \)で含む原料液(物質\( \rm{B} \)を含まない)を, 体積が\( V \)となるまで両容器に満たす。その後, 反応器Ⅰでは, 反応開始時刻を\( t=0 \)として, 一定温度\( T \)で反応を進行させる。一方, 反応器Ⅱでは, 同じ温度\( T \)で反応を開始させると同時に, 以後は反応温度を\( T \)に保ちながら, 原料液を一定の流量\( F \)(単位時間あたりに流れる液の体積)で連続的に反応器に供給し, 出口から同じ流量\( F \)で反応液を流出させる。両反応器は十分かくはんされており, 反応器内の物質量濃度は均一とする。また, 反応による体積変化はないとする。
実験1:反応式(1)に従う不可逆反応の場合
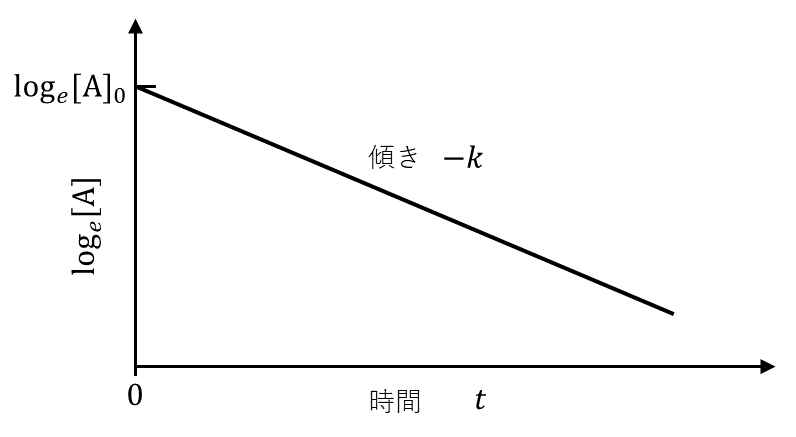
反応器Ⅰにおいて, \( \rm{A} \)の濃度(\( [\rm{A}] \))の時間変化を測定し, \( \log_e [\rm{A}] \)(ただし, \( e \)は自然対数の底であり, 値は\( 2.718\cdots \)である)と反応時間(\( t \))の関係を調べたところ, 図2に示すような直線関係が得られ, その直線の傾きは, \( -k \)であった。この関係式を式で表せば\( \log_e [\rm{A}] = \)アとなる。これより, 反応開始時から\( \rm{A} \)の半分が反応するまでの時間はイで与えられ, \( [\rm{A}]_0 \)に依存しないことがわかる。また, この時刻における生成物\( \rm{B} \)の物質量はウである。
一方, 反応器Ⅱを用いた実験では, 反応開始後十分な時間が経過した後は, 反応器内のすべての物質濃度は一定になり, \( [\rm{A}] = \frac{[\rm{A}]_0}{2} \)となった。このとき, 反応(1)における物質\( \rm{A} \)の反応速度は図2の結果より\( k[\rm{A}] \)で与えられるから, 単位時間あたりに反応により消失する\( \rm{A} \)の物質量はエとなる。また, 単位時間に流出する\( \rm{A} \)の物質量はオ, 単位時間に流入する\( \rm{A} \)の物質量はカで与えられ, これらの間には
エ \( + \) オ \( = \) カ
という物質量のつりあいの関係式が成り立つ。この関係から, 流量\( \rm{F} \)はキとなる。また物質\( \rm{A} \)の濃度が\( \frac{[\rm{A}]_0}{2} \)で一定になった状態でイと同じ時間だけ実験をつづけたとき, この間に流出液から得られる生成物\( \rm{B} \)の物質量はウのク倍である。
実験2:反応式(2)に従う可逆反応の場合
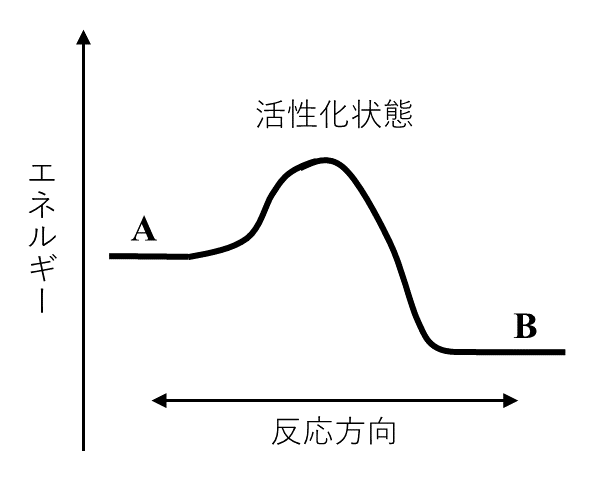
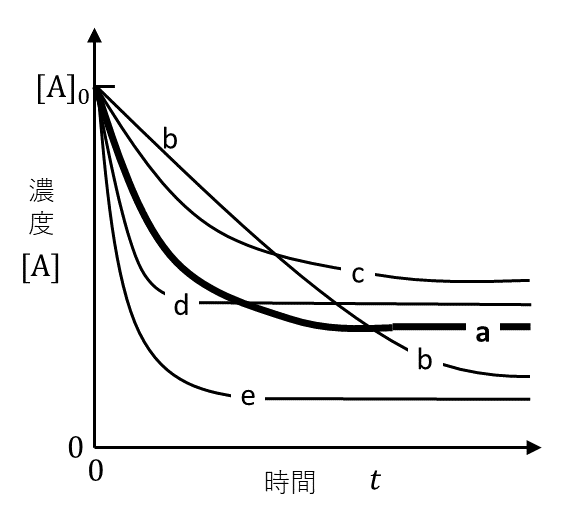
反応(2)の正反応における\( \rm{A} \)の反応速度は\( k_1[\rm{A}] \), 逆反応における\( \rm{A} \)の生成速度は\( k_2[\rm{B}] \)でそれぞれ与えられる。また, 反応の進行方向に沿ったエネルギーの変化は図3に示したとおりとする。反応器Ⅰにおいて, \( \rm{A} \)の濃度は, 反応時間とともに図4の太い実線\( \rm{a} \)のように変化し, ①十分な反応時間が経過したのち一定になった。この平衡状態で正逆両反応の速度は等しくなることから, 可逆反応(2)の平衡定数\( K \)は, 反応速度定数\( k_1, k_2 \)を用いて\( K = \)ケと表される。
一方, 反応器Ⅱを用いた実験でも, 十分な時間が経過した後には, 物質\( \rm{A} \), \( \rm{B} \)の濃度は一定になった。この時の濃度をそれぞれ\( \rm{[A]_S} \), \( \rm{[B]_S} \)とすると, 生成物\( \rm{B} \)の物質量に関するつりあいの関係式はコとなる。この関係式と\( K = \)ケの関係を用いると, \( S = \frac{\rm{[B]_S}}{\rm{[A]_S}} \)という比と平衡定数\( K \)の間には次の関係式が成り立つ。
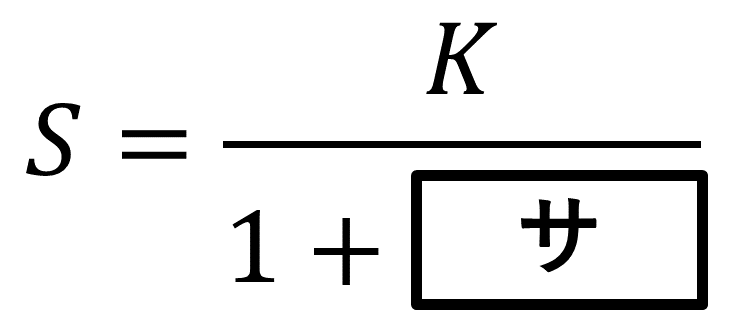
この式より, \( S \)の値は常に\( K \)の値より小さく, 流量\( F \)が小さくなるにつれ\( K \)に近づくことがわかる。
問1 文中のア~サに適切な数式を記入せよ。
問2 実験2の下線部①で記した物質\( \rm{A} \)の一定濃度は\( \frac{[\rm{A}]_0}{3} \)であった。可逆反応(2)の温度\( T \)における平衡定数\( K \)の値を求めよ。
問3 実験2において, 反応器Ⅰを用いた実験を\( T \)より高い温度と, \( T \)より低い温度で行った。このとき, 物質\( \rm{A} \)の濃度の時間変化は, \( T \)より高い温度では図4に示す曲線シとなり, \( T \)より低い温度では曲線スとなった。図4の中からシとスに入る適切なものを選び, \( \rm{b} \) ~ \( \rm{e} \)の記号で答えよ。
解説
不可逆反応と可逆反応, 反応器Ⅰと反応器Ⅱ, 組み合せて\( 2 \times 2 = 4 \)通りの場合があり, 順番に考察する流れになっている。反応器Ⅱでは, 「単位時間あたり」の量を使用しているので, 単位に注意しなければならない。ここでは仮に単位時間を\( [s] \)としておき, わかりにくいところは単位を明示して考えることにする。例えば流量\( F \)は, 単位時間あたりに流れる液の体積だから, \( F[l/s] \)である。
実験1:反応器Ⅰ
ア
図2のグラフは縦軸が\( \log_e [\rm{A}] \), 横軸が\( t \)であり, 切片\( \log_e [\rm{A}]_0 \), 傾き\( -k \)の直線だから, \( \log_e [\text{A}] = \log_e [\text{A}]_0 -kt \)。
イ, ウ
\( \rm{A} \)の半分が反応するときの表は以下の通り。
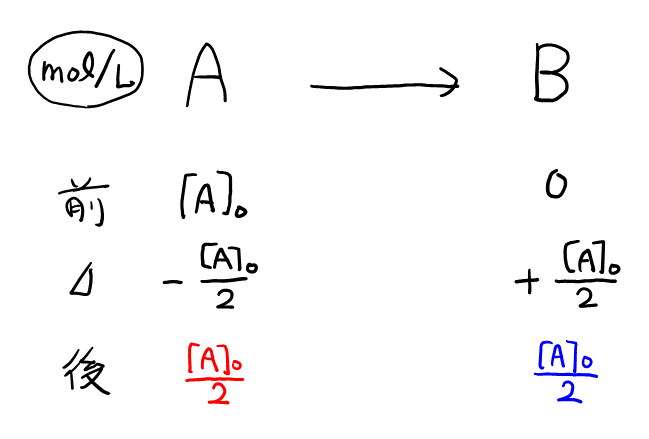
アの式で, 縦軸の\( \log_e [\rm{A}] \)を\( \log_e \color{red}{\frac{[\rm{A}]_0}{2}} \)として\( t \)を求めると, \( t = \frac{\log_e 2}{k} \)。
このときの\( \rm{B} \)の物質量は, \( \color{blue}{\frac{[\rm{A}]_0}{2}} \times V \)。
実験1:反応器Ⅱ
エ
反応速度は, 「単位時間当たりの濃度の変化」であるから, 単位は\( [\text{mol} / (\color{red}{l} \cdot s)] \)であることに注意。
エで求めるものは単位時間当たりの物質量(\( [\text{mol} / s] \))だから, 反応速度\( k[\text{A}] = \frac{1}{2}k[\text{A}]_0 \)に, 体積\( V[\color{red}{l}] \)をかければよい。
オ, カ
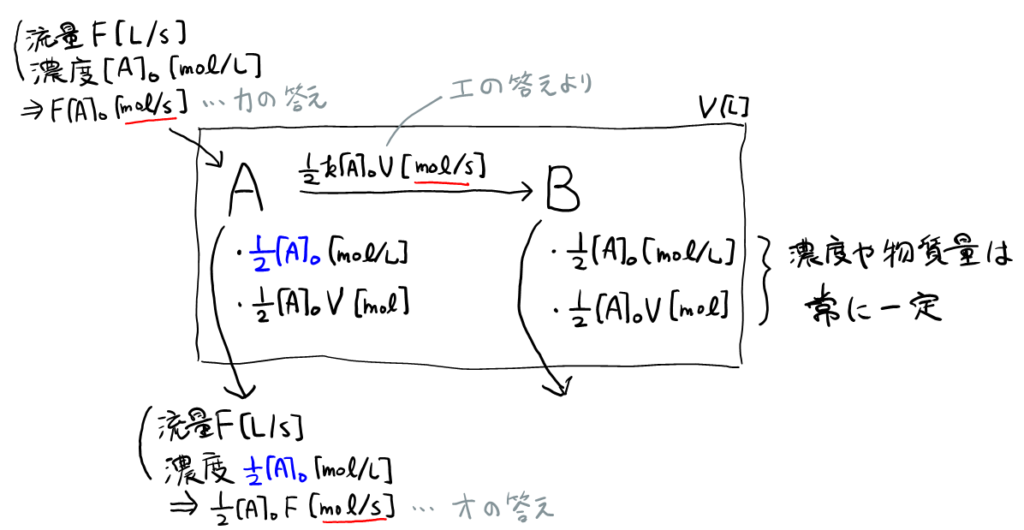
流入・流出については, 単位を明記すると図5のようになる。
キ
与えられたつりあいの関係式を解くだけ。つりあいの関係式が, 図5で\( \rm{A} \)を中心とした図と対応していることも確認しておこう。結果は\( F = kV \)となる。
また検算のため, 単位を確認しておくことをおすすめする。左辺の\( F \)は, はじめに述べたとおり, \( [l/s] \)。右辺の\( V \)はもちろん\( [l] \)。右辺の\( k \)は, イより\( k = \frac{\log_e 2}{t} \)となり, \( \log_e 2 \)は無次元の定数であるから, \( k \)の単位は\( [/s] \)。よって, 確かに右辺の単位も\( [l/s] \)となっている。
ク
図5を見ると, 十分時間経過後では\( \rm{A} \)と\( \rm{B} \)の濃度や物質量が等しいので, 単位時間あたりに流出する物質量も, \( \rm{A} \)と\( \rm{B} \)で等しいことがわかる。あとは, 時間イを掛けると総物質量となり, ウの答えとの比を取ればよいだけ。キの関係式も使うと, 答えは\( \log_e 2 \)倍となる。
実験2:反応器Ⅰ
ケ
典型問題。定義より\( K = \frac{[\text{B}]}{[\text{A}]} \)であり, 速度が等しいという条件\( k_1[\text{A}] = k_2[\text{B}] \)を使うと, \( K = \frac{[\text{B}]}{[\text{A}]} = \frac{k_1}{k_2} \)。
問2
物質\( \rm{A} \)が一定濃度\( \frac{[\rm{A}]_0}{3} \)となったときの表は以下の通り。
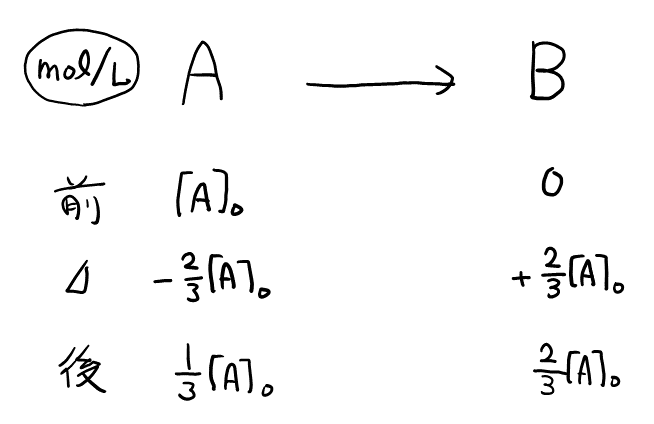
よって, \( K = \frac{[\text{B}]}{[\text{A}]} = \frac{2/3}{1/3} = 2 \)。
問3
図3より, \( \ce{A -> B} \)の反応は, \( \text{A} = \text{B} + Q(Q > 0) \)と書ける発熱反応だとわかる。
高温にしたときは, 発熱しすぎないように左向きに平衡が移動し, \( \rm{A} \)の量が増える。よってcかd。またそもそも高温にすると反応速度は上がるので, cとdのうちで反応速度が速いのはdである。
低温にしたときも, 同じように2段階で考えると, 答えはbとなる。
実験2:反応器Ⅱ
コ
誘導に従い物質\( \rm{B} \)の収支について考える。\( \rm{A} \)と異なり\( \rm{B} \)は流入はないので, ①流出量, ②反応によって増える量, ③反応によって減る量, を考えればよい。図を書くと以下のようになる。
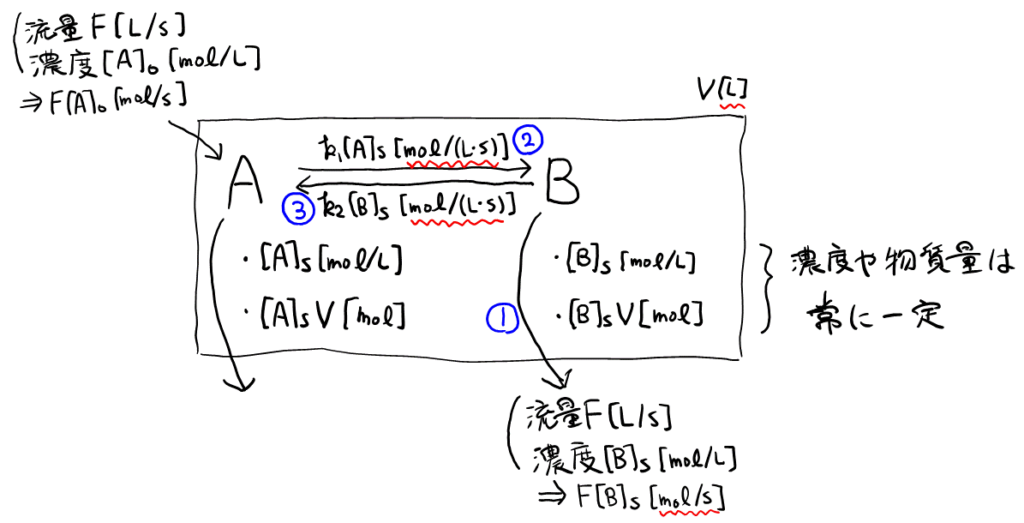
①②③それぞれ, 単位時間当たりの物質量の増減と考えて, 単位に注意して計算すると, 以下のようになる。
①:\( [\text{B}]_\text{S}[\text{mol}/l] \times F[l/s] = F[\text{B}]_\text{S}[\text{mol}/s] \)。
②:\( k_1[\text{A}]_\text{S}[\text{mol}/(l \cdot s)] \times V[l] = k_1V[\text{A}]_\text{S}[\text{mol}/s] \)。
③:\( k_2[\text{B}]_\text{S}[\text{mol}/(l \cdot s)] \times V[l] = k_2V[\text{B}]_\text{S}[\text{mol}/s] \)。
①+③=②より, 答えは\( F[\text{B}]_\text{S} + k_2V[\text{B}]_\text{S} = k_1V[\text{A}]_\text{S} \)となる。
サ
直前の式より\( (F + k_2V)[\text{B}]_\text{S} = k_1V[\text{A}]_\text{S} \)だから, \( \frac{[\text{B}]_\text{S}}{[\text{A}]_\text{S}} = \frac{k_1V}{F + k_2V} \)と変形でき, 分母分子を\( k_2V \)で割ると, 与えられた形となる。答えは\( \frac{F}{k_2V} \)。
振り返り
反応器Ⅱでつりあいの関係式を立てるところが多少難しいので, ここで差が付くと思われる。単位に注意して, 図を書いて考えることが大切。
また逆に言えば, 問2や問3は反応器Ⅰに関する問題で簡単なので, 取り逃してはいけない。
コメント