問題
次の文を読んで, 問1~問5に答えよ。
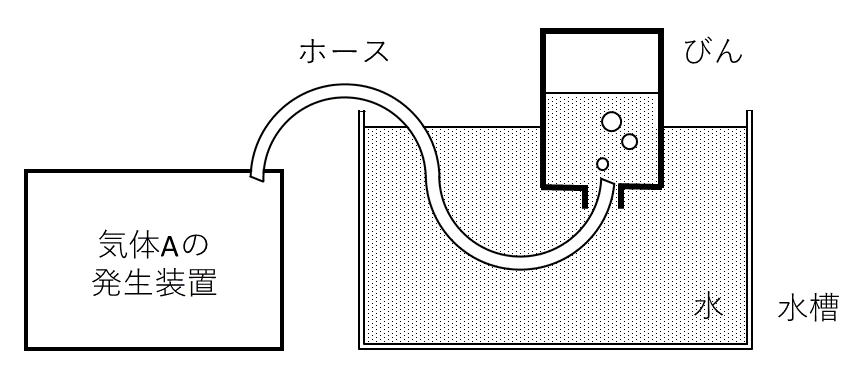
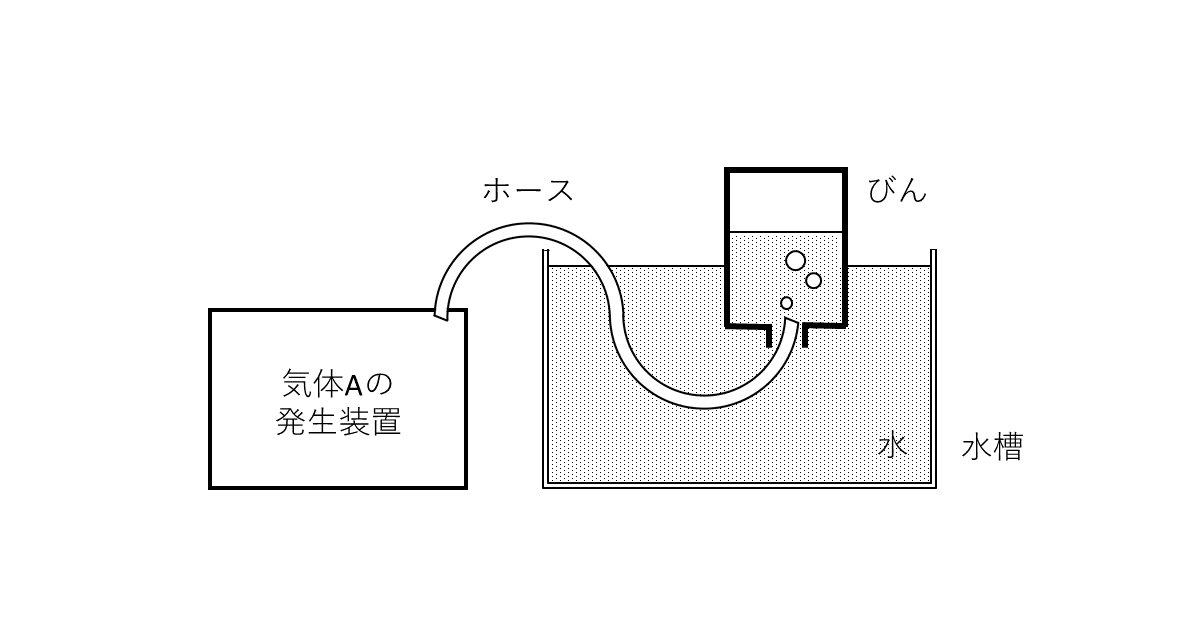
気体発生装置を用いて発生させた物質量\( N[\rm{mol}] \)の気体\( \rm{A} \)を図1に示すようにびんの中に捕集したのち, ホースを水槽から抜いた。その後, 温度\( T[\rm{K}] \)に保ち, びんを動かすことなく十分な時間保持すると, ビンの中には新たに気体\( \require{mhchem} \ce{A2} \)が生成し, 次の平衡が達成された。
$$ \ce{A + A <-> A2} \tag{1} $$
①このとき, びんの中の気体部分の体積は\( V[\rm{L}] \), 圧力は\( P[\rm{atm}] \)であった。(図2)
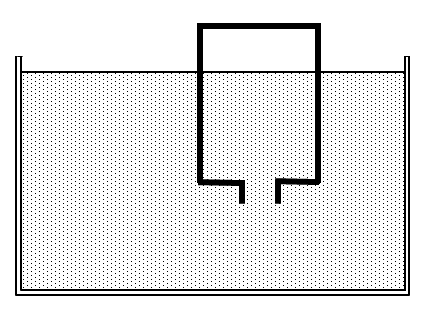
次に, 同じ温度\( T[\rm{K}] \)で, 反応(1)の平衡が達成されている状態を保ちながら, びんをゆっくりと押し下げて②びんの中の水面と水槽の水面を一致させた。(図3)
ただし, びんの中での水の気液平衡は常に成り立っているものとする。気体\( \ce{A} \), \( \ce{A2} \)はともに水に溶けず, 水蒸気, 気体\( \ce{A} \), \( \ce{A2} \)はすべて理想気体と考えてよい。また, 大気圧を\( P_0[\rm{atm}] \), 温度\( T[\rm{K}] \)での水蒸気圧を\( P_W[\rm{atm}] \), 水の密度を\( d_W[\rm{g/cm^3}] \), 気体定数を\( R[\rm{atm \cdot L / (K \cdot mol)}] \)とする。
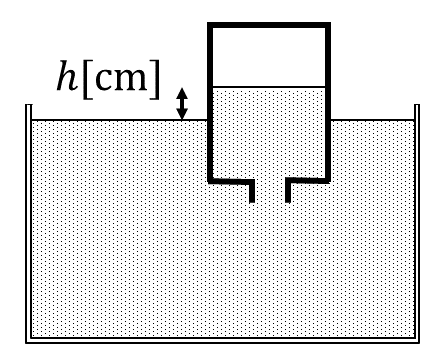
問1 図2におけるびんの中の水面と水槽の水面との差\( h[\rm{cm}] \)を, 水銀の密度\( d[\rm{g/cm^3}] \)および本文中の記号(\( N, T, V, P, P_0, P_W, d_W, R \))のうちで適切なものを用いて表せ。ただし, \( 1 \rm{atm} = 760 \rm{mmHg} \)とする。
問2 下線部①において, びんの中にある気体\( \rm{A} \)の物質量\( N_1[\rm{mol}] \)を, 本文中の記号のうちで適切なものを用いて表せ。
問3 下線部①において, 反応(1)の平衡定数\( K[1/(\rm{mol/L})] \)を, \( N, N_1, V \)を用いて表せ。
問4 温度が一定ならば平衡定数\( K \)が一定であるとして, 下線部②において, びんの中の水面と水槽の水面を一致させたとき, びんの中にある気体\( \rm{A} \)の物質量\( N_2[\rm{mol}] \)を, \( K \)および本文中の記号のうちで適切なものを用いて表せ。
問5 \( N_1 \)と\( N_2 \)の関係について適切なものを, 次の(ア)~(ウ)のうちから1つ選べ。
(ア) \( N_1 > N_2 \)
(イ) \( N_1 = N_2 \)
(ウ) \( N_1 < N_2 \)
解説
問1
水銀柱を使った圧力の換算を今一度確認しておく。以下の図のように, 水銀柱の\( 760\rm{mm} \)分の圧力が, 基準の圧力(\( 1\rm{atm} \))となる。水銀の重さは水の約\( 14 \)倍であるから, 水柱に置き換えると, 水銀の場合よりもたくさんの水が必要で, 対応する水柱の高さが約\( 14 \)倍になる。本問では, 水と水銀の密度が与えられているので, 約\( 14 \)倍のところが\( \frac{d}{d_W} \)倍となる。
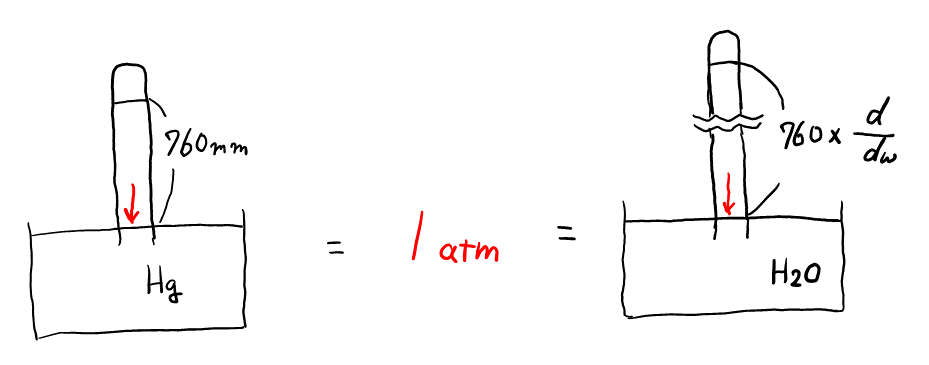
あとはただの比例計算で,
$$ 水の76 \times \frac{d}{d_W}[\rm{cm}]分の圧力 : 水のh[\rm{cm}]分の圧力 = 1[\rm{atm}] : ?[\rm{atm}] $$
より, 水の\( h[\rm{cm}] \)分の圧力に対応する\( [\rm{atm}] \)が求められる(\( \frac{hd_W}{76d}[\rm{atm}] \))。
この換算が出来れば, 水面での圧力のつり合いの式を立てて終了。
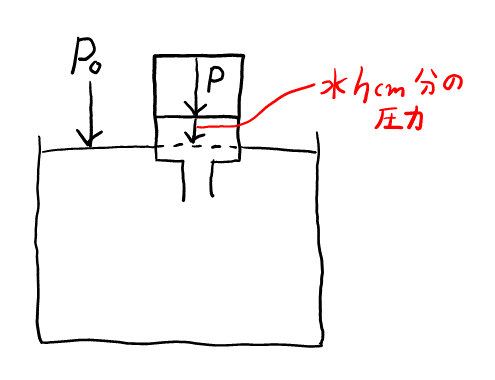
図より, \( P_0 = P + \color{red}{\frac{hd_W}{76d}} \)。
問2
まず, 物質量の変化を追うことができる。
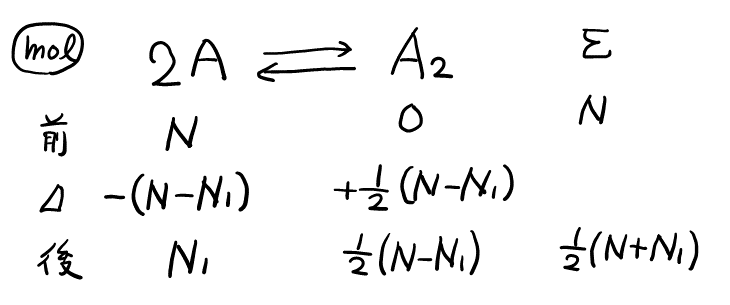
ここで, 水蒸気圧が与えらえれているので, 水蒸気圧を考慮しなければならない。下線部①の平衡時にびんの中の圧力が\( P \)なので, この圧力は, 水蒸気圧, 気体\( \ce{A} \)の分圧, 気体\( \ce{A2} \)の分圧の合計である。
\( P = P_W + \color{red}{P_A + P_{A_2}} \)
状態方程式は, 混合気体\( \ce{A} \) + \( \ce{A2} \)について立てる。
\( (\color{red}{P – P_W})V = \frac{1}{2}(N+N_1)RT \)
問3
省略。
問4
実際には「初期状態→下線部①→下線部②」のように変化したが, \( \rm{mol} \)の変化を追う際は, 下線部①を経由しなくても, 「初期状態→下線部②」と考えても同じである。よって以下のように, \( N_1 \)を使わずに直接変化の表が書ける。
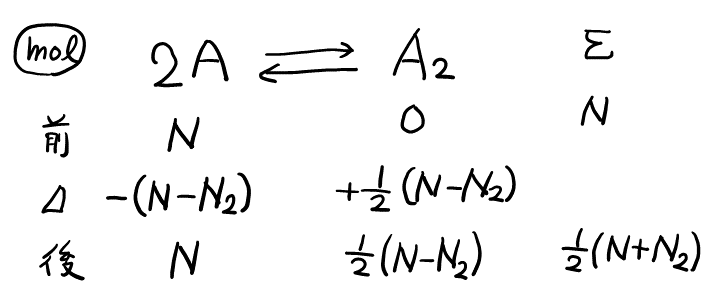
問2と同様に, 水蒸気圧に注意して等式を立てると, 以下のようになる。
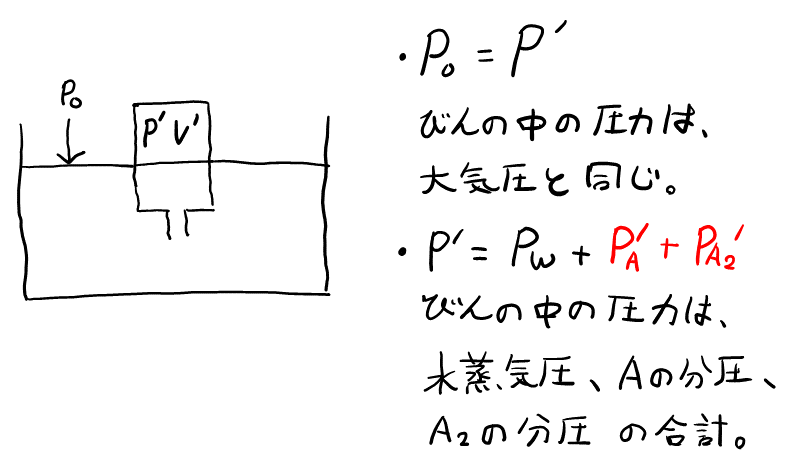
再び混合気体\( \ce{A} \) + \( \ce{A2} \)について状態方程式を立てると,
\( (\color{red}{P_0 – P_W})V’ = \frac{1}{2}(N+N_2)RT \)
より\( V’ \)が求まるので, 平衡定数の式に代入して終了。
問5
問2と問4の答えを比較してもよいが, 式の形が異なるので追加で式変形が必要となり, 非常に煩雑になる。ここでは定性的に答えを出すことが求められている。
びんを押し込むと, 中の気体の体積は減る(頭の中で想像してみるとほぼ明らか)。よって, 体積が増える方向に平衡が移動する。
振り返り
全体を通じて水蒸気圧の扱いに注意が必要。また, 問1の単位の換算から間違える人も一定数いる。気体の扱いに慣れている人とそうでない人で, 大きく差が付いたと思われる。
コメント