問題
次の文(a), (b)を読んで, 問1~問4に答えよ。解答はそれぞれ所定の解答欄に記入せよ。
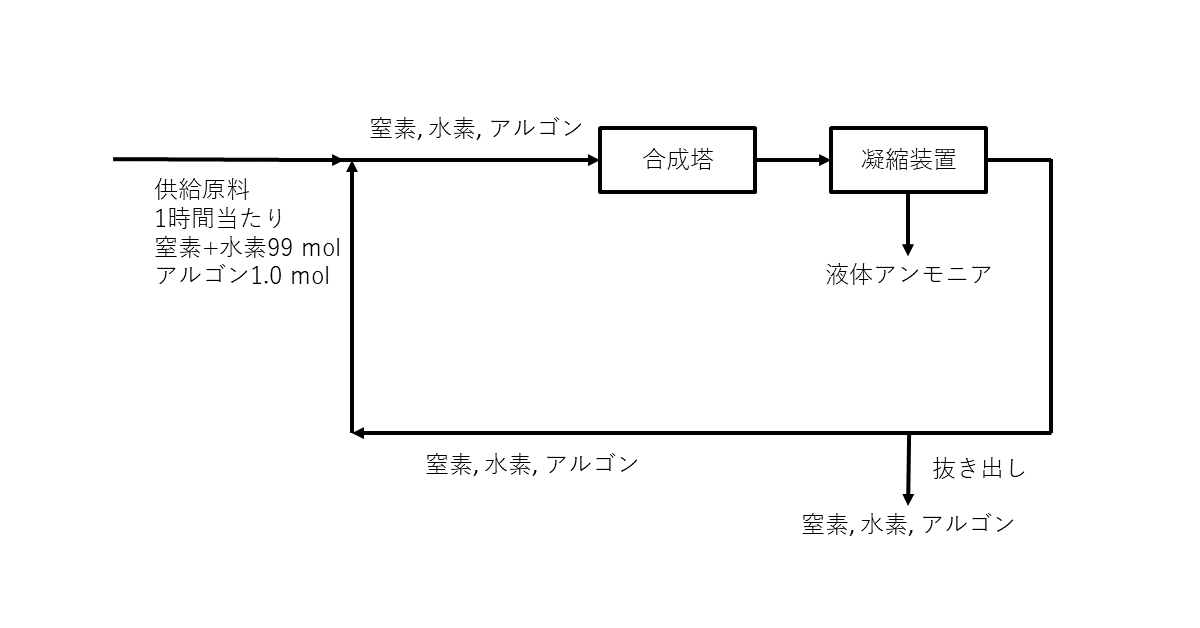
(a) アンモニアは, 工業的には窒素と水素から直接合成される。連続的にアンモニアを製造するには, 図1に示すように, アンモニア合成塔で窒素と水素を直接反応させ, 生成したアンモニアのみを凝縮させて液体として全量を分離し, 残った未反応気体は新しい原料とともに合成塔に戻される。原料の窒素には, 窒素の製造過程で混入するアルゴンが不純物として含まれるので, 合成塔内でのその蓄積を防ぐために凝縮装置から出てくる未反応気体を一定の量だけ外部に抜き出す。
いま, 原料を\( 1 \)時間当たり\( 100\rm{mol} \)供給しながら連続的に反応させた。原料\( 100\rm{mol} \)には不純物としてアルゴンが\( 1.0\rm{mol} \)含まれ, 他は物質量比\( 1:3 \)の純粋な窒素と水素であった。十分な時間が経過して\( 1 \)時間当たりの液体アンモニアの生成量が一定となったとき, 合成塔に入る窒素と水素の物質量の合計とアルゴンの物質量の比{(窒素 + 水素) : アルゴン}は\( 25:1 \)となり, 合成塔では窒素と水素の物質量のそれぞれ\( 20 \% \)が反応で減少してアンモニアが生成した。合成塔および凝縮装置の前後でアルゴンの物質量は変化しないので, 凝縮装置から出てくる窒素と水素の物質量の合計とアルゴンの物質量の比{(窒素 + 水素) : アルゴン}はア\( :1 \)になり, 凝縮装置から出てくる未反応気体のうち合成塔に戻される窒素と酸素の物質量の合計を\( 1 \)時間当たり\( y[\rm{mol}] \)とすると, 合成塔に供給される気体に対しては
\( (99+y) : (y / \) ア \( + 1.0) = 25 : 1 \)
が成り立つ。したがって, \( y= \)イになり, アンモニアの生成量は\( 1 \)時間当たりウ\( \rm{mol} \)となる。なお, 抜き出される窒素と水素の物質量の合計は\( 1 \)時間当たりエ\( \rm{mol} \)となる。このように, 合成塔から出てくる未反応気体を循環して利用することにより, 効率よくアンモニアを合成できることがわかる。
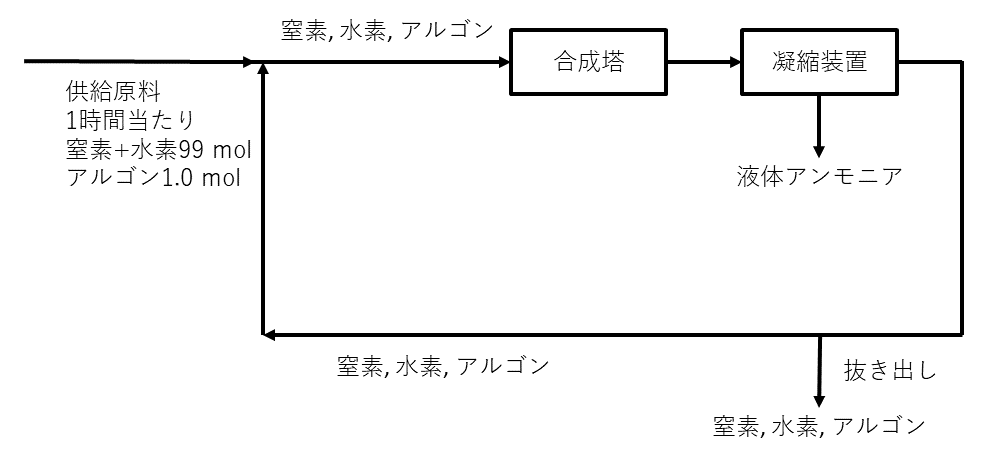
問1 文中のア~エに適切な数値を有効数字\( 2 \)けたで記入せよ。
(b) アンモニアは, 実験室では, 塩化アンモニウムと水酸化カルシウムの混合物を加熱して合成し, オ置換で捕集する。アンモニアは三角錐形の分子であり, 分子内の共有電子対は, カ原子側にひきつけられ, かなり強い極性をもつ。アンモニアが同じ\( 15 \)族元素の水素化合物であるホスフィン(\( \require{mhchem} \ce{PH3} \))やアルシン(\( \ce{AsH3} \))に比べて高い沸点をもつのは, アンモニア分子の窒素原子と, 他のアンモニア分子の水素原子との間に弱い結合ができているためである。この結合は特にキ結合とよばれる。また, アンモニア分子の窒素原子の非共有電子対と水素イオンとの共有結合によってアンモニウムイオンが生じる。この共有結合は特にク結合とよばれる。
問2 文中のオ~クに適切な語句を記入せよ。
問3 アンモニアと水素イオンからアンモニウムイオンが生成する。その反応式を電子式を用いて記せ。
問4 ある触媒を用いてアンモニアを熱分解すると, 窒素と水素が生じる。いま, 触媒の入った真空容器に気体のアンモニアを入れ温度を\( T_1[\rm{K}] \)に保った。その後温度を\( 2T_1[\rm{K}] \)まで上げてこの温度を一定の時間保つと, 容器に入れたアンモニアが熱分解し, 容器内の圧力は温度が\( T_1[\rm{K}] \)のときの\( 3.5 \)倍になった。このとき, アンモニアは物質量で何\( \% \)分解したかを有効数字\( 2 \)けたで答えよ。なお, 触媒の体積は無視でき, 容器内の体積は温度によって変化しないものとする。また, 気体はすべて理想気体とする。
解説
(a)
まずは文章をよく読み, 状況を掴む。分かったことから, 少しずつ図に書き込んでいく。(窒素+水素)はまとめて考えたほうがよいこと, すべて1時間当たりの物質量で考えればよいことなどを確認しておく。
まず, 合成塔に入る部分について, 比が\( 25:1 \)と明示されているので, そこから考えていく。合成塔に入る1時間当たりのアルゴンの物質量(以降, 単位\( \rm{mol / h} \)は省略)を\( x \)とすると, 合成塔に入る(窒素+水素)は\( 25x \)となる。合成塔で(窒素+水素)が\( 20 \% \)減少したところまで書くと, 以下のようになる。
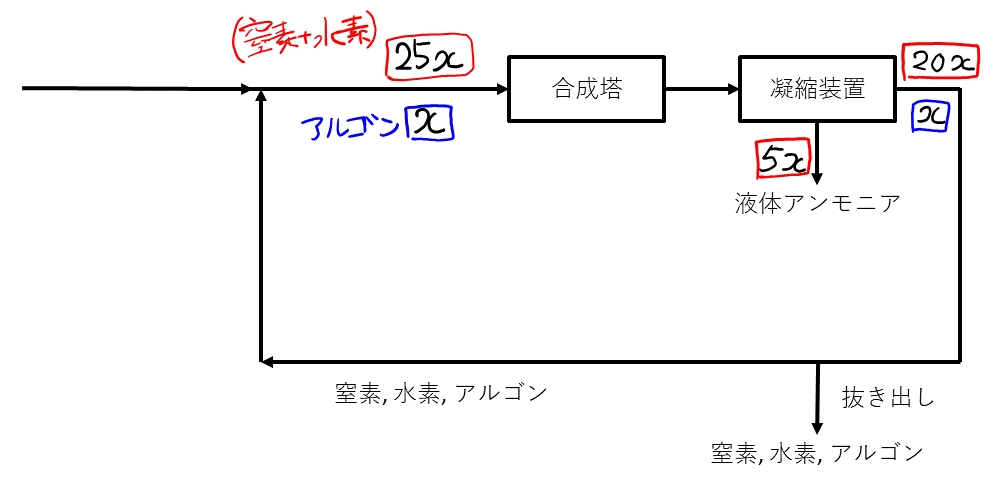
図より, アは\( 20 \)。これが求まれば, 文中の式
\( (99+y) : (y / \) ア \( + 1.0) = 25 : 1 \)
について考察するまでもなく, \( y \)が計算できる(\( y = 296 \))。
次に, 図の下側を埋めていく。合成塔に戻される(窒素+水素)が\( y \)であることから, 抜き出されたのは\( 20x – y \)だとわかる。抜き出される気体の比は, 合成塔から出てきたばかりで\( 20:1 \)だから, 抜き出されたアルゴンの量もわかる(\( 20x – y \)の\(\frac{1}{20}\))。よって, 抜き出されなかった(合成塔に戻される)アルゴンは, 残りの\( \frac{1}{20}y \)である。
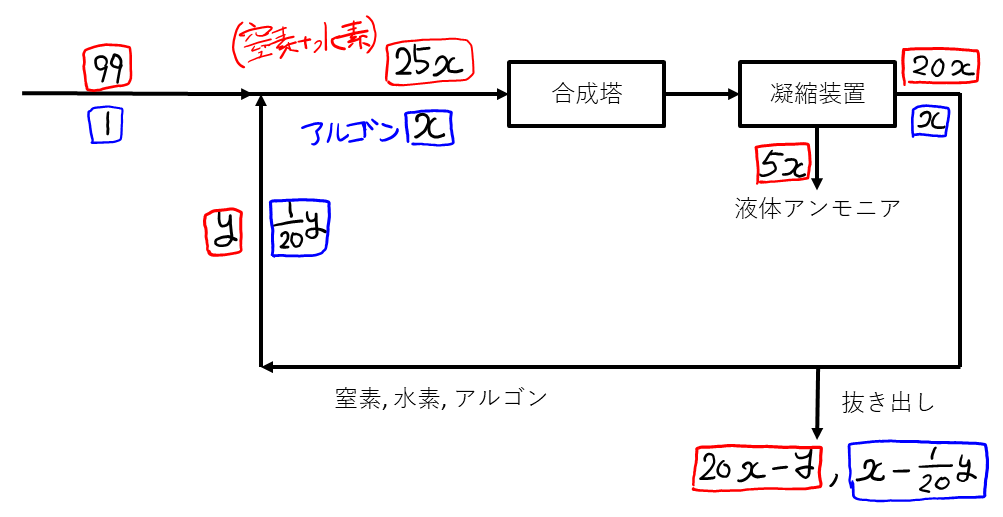
この図から, 合成塔に入る(窒素+水素)について\( \color{red}{99} + \color{red}{y} = \color{red}{25x} \), アルゴンについて\( \color{blue}{1} + \color{blue}{\frac{1}{20}y} = \color{blue}{x} \)という等式が立てられて, 比を取ると文中の式になることが確認できる。
\( y \)が分かっているので\( x \)が求まる(\( x = 15.8 \))。ウは\( 5x \)の部分であるが, \( \ce{N2 + 3H2 -> 2NH3} \)より, アンモニアの生成量は, \( 5x \)の\( \frac{2}{4} \)倍であることに注意。
エの抜き出される(窒素+水素)は, 先述の通り\( 20x – y \)で, すでに\( x \)と\( y \)が出ているので計算できる。
(b)
問2
オ
アンモニアの捕集方法は, もちろん上方置換。高校範囲では, 上方置換を使うのはアンモニアだけ。
カ
共有電子対は, 電気陰性度が大きい原子の方に引き寄せられる。\( \ce{H} \)と\( \ce{N} \)ではもちろん\( \ce{N} \)の方が大きい。
電気陰性度の基本について念のための確認。電気陰性度は, イオン化エネルギーと電子親和力の総合力と考えられるが, 一般にイオン化エネルギー\( \gg \)電子親和力なので, 電気陰性度の大小はイオン化エネルギーの大小とほぼ同じ。どちらも, 周期表の右上に行くほど大きい。
キ
水素結合は, 周期表の右上の原子である\( \ce{N}, \ce{O}, \ce{F} \)が\( \ce{H} \)と出会ったときに出来る。
問題文にあるように, 水素結合ありと水素結合なしでは, 当然水素結合ありの方が強い(沸点が高い)が, 発展として, 水素結合あり同士の比較もよく問われる。\( \ce{NH3}, \ce{H2O}, \ce{HF} \)の中で一番強いのは, 1原子当たり水素結合が2つ出来る\( \ce{H2O} \)である。
問2ク, 問3
共有結合の作り方は2種類ある。1つ目は, 原子Aと原子Bが, それぞれ不対電子を出し合って, 共有結合を作る方法。2つ目は, 原子Aの非共有電子対が, 原子Bの空軌道に入る方法(AとBの役割を入れ替えても同じ)。
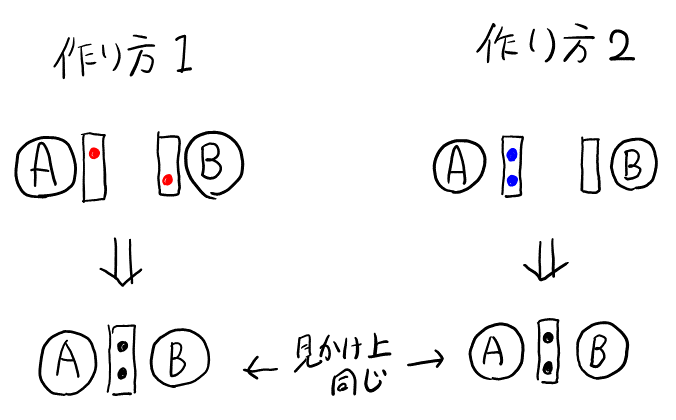
後者の作り方で出来た共有結合を, 配位結合と呼ぶ。
ただし, 上の図より明らかな通り, 共有結合を作ってしまえば, それがどちらの作り方で出来たのか判別することは出来ない。
問4
最初の\( \ce{NH3} \)の物質量を\( n \), 分解率を\( \alpha \)として表を書くと,
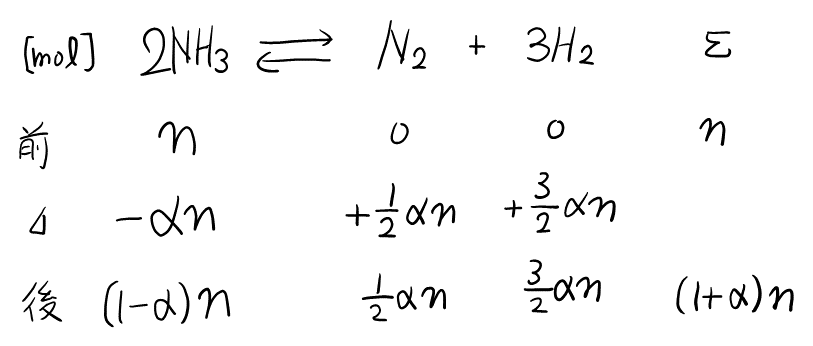
分解後の物質量が表せたので, 分解前と分解後で状態方程式を立てられる。分解前の圧力を\( P \)(分解後は\( 3.5 \)倍), 体積を\( V \)(常に一定)とすると,
分解前 : \( PV = nRT_1 \)
分解後 : \( 3.5PV = (1+\alpha)nR \cdot 2T_1 \)
より, 辺々割って\( \alpha \)が求まる。
振り返り
(a)は, ただの算数の問題だが, どこに着目すればよいかわかりにくいので, 実際の試験では多くの受験生が難問と感じたと思われる。一方(b)は, 問4も含めて基本問題であるので, こちらは絶対に落としてはいけない。
物理や化学は, その科目とは直接関係が無い, 読解力と算数力だけの問題がしばしば出題される。過去問を通じて慣れていくしかない。
コメント