問題
(1) 変数\( t \)が\( t>0 \)の範囲を動くとき
\begin{align}
&f(t) = \sqrt{t} + \frac{1}{\sqrt{t}} + \sqrt{t + \frac{1}{t} + 1} \\
&g(t) = \sqrt{t} + \frac{1}{\sqrt{t}} – \sqrt{t + \frac{1}{t} + 1}
\end{align}
について, \( f(t) \)の最小値は\( 2 + \sqrt{3} \), \( g(t) \)の最大値は\( 2 – \sqrt{3} \)であることを示せ。
(2) \( a = \sqrt{x^2 + xy + y^2}\), \( b = p\sqrt{xy} \), \( c = x + y \)とおく。任意の正数\( x, y(>0) \)に対して, \( a, b, c \)を\( 3 \)辺の長さとする三角形がつねに存在するように, \( p \)の値の範囲を定めよ。
発想
(1)は, 式がややこしいので, まずはよく観察する。そのまま微分するのは最終手段。
(2)は, 明らかに三角形の成立条件を使う問題。三角形の成立条件では, 辺の大小が分かっていれば条件がシンプルになるので, 辺の大きさを比べると, 常に\( c>a \)であることが分かる。また, (1)と同様に式を観察すると, 全て次数が同じことに気づくので, 変数の数を減らせそう。
(1)の下書き
気付くことをまとめると, 以下のようになる。
- \( \square + \frac{1}{\square} \)の形が多い→相加相乗が使えそう
- 同じ形が出てくるので, まとめられそう→\( \underline{\sqrt{t} + \frac{1}{\sqrt{t}}} = x \)と置き換えると, \( x^2 = \underline{t + \frac{1}{t}} + 2 \)となってお得
- \( f(t) = \square + \triangle, g(t) = \square – \triangle \)の形をしているので, \( f(t)g(t) = \square^2 – \triangle^2 \)が楽に計算できそう
相加相乗を使う場合
\( f(t) \)に相加相乗平均の大小関係を用いると,
$$\begin{eqnarray}
f(t) &=& \color{red}{\sqrt{t} + \frac{1}{\sqrt{t}}} + \sqrt{\color{blue}{t + \frac{1}{t}} + 1} \\
&\geqq& \color{red}{2\sqrt{\sqrt{t} \cdot \frac{1}{\sqrt{t}}}} + \sqrt{\color{blue}{2\sqrt{t \cdot \frac{1}{t}}} + 1} \\
&=& 2\sqrt{1} + \sqrt{2\sqrt{1} + 1} \\
&=& 2 + \sqrt{3}
\end{eqnarray}$$
となる。もちろん, ここから直ちに最小値が\( 2 + \sqrt{3} \)であるとは言えない(\( x^2 \geqq -1000 \)だからといって, \( x^2 \)の最小値は\( -1000 \)と言えないのと同じ)ので, 等号成立条件を調べて, \( \sqrt{t} = \frac{1}{\sqrt{t}} \)かつ\( t = \frac{1}{t} \)が成り立つ\( t \)が存在するかどうかを調べる。\( t=1 \)で成り立つのでOK。
次に\( g(x) \)の最大値。同様に相加相乗を使って求めようとすると, 等号の向きがそろわないので, うまく行かない。ここで, \( f(x) \)を上手く使う。最初に観察したように, \( f(x) \)と\( g(x) \)の積は, 2乗の差の公式で計算できそうなので計算してみると,
$$\begin{eqnarray}
f(t)g(t) &=& \left( \sqrt{t} + \frac{1}{\sqrt{t}} + \sqrt{t + \frac{1}{t} + 1} \right) \left( \sqrt{t} + \frac{1}{\sqrt{t}} – \sqrt{t + \frac{1}{t} + 1} \right) \\
&=& \left( \sqrt{t} + \frac{1}{\sqrt{t}} \right)^2 – \left( \sqrt{t + \frac{1}{t} + 1} \right)^2 \\
&=& \left( t + \frac{1}{t} + 2 \right) – \left( t + \frac{1}{t} + 1 \right) \\
&=& 1
\end{eqnarray}$$
よって, \( g(t) = \frac{1}{f(t)} \)となる(\( f(t) \neq 0 \)の確認は必ず必要)ので, \( f(t) \)が最小値\( 2 + \sqrt{3} \)をとるときに\( g(t) \)は最大値となり, その値は\( \frac{1}{2 + \sqrt{3}} = 2 – \sqrt{3} \)となる。
置き換えを使う場合
\( \sqrt{t} + \frac{1}{\sqrt{t}} = x \)と置くと, \( x^2 = t + \frac{1}{t} + 2 \)すなわち\( t + \frac{1}{t} = x^2 – 2 \)となるので, \( f,g \)をそれぞれ\( x \)の関数として, \( f(x) = x + \sqrt{x^2 – 1} \), \( g(x) = x – \sqrt{x^2 – 1} \)と表せる。
ここで, 置き換えをしているので, 改めて\( x \)の定義域の確認が必要。\( t>0 \)の範囲で, \( x = \sqrt{t} + \frac{1}{\sqrt{t}} \)の取りうる範囲は, グラフを書いてもよいが, 相加相乗より, \( x \geqq 2\sqrt{\sqrt{t} \cdot \frac{1}{\sqrt{t}}} = 2 \)である。
あとは, \( x \geqq 2 \)の範囲で, \( f(x) = x + \sqrt{x^2 – 1} \), \( g(x) = x – \sqrt{x^2 – 1} \)の増減を調べればよいだけ。\( t \)の関数のままよりもずっと楽に計算できる。
$$\begin{eqnarray}
f'(x) &=& 1 + \frac{2x}{2\sqrt{x^2-1}} \\
&=& \frac{\sqrt{x^2-1} + x}{\sqrt{x^2-1}} > 0 (\because x \geqq 2)
\end{eqnarray}$$
より, \( f(x) \geqq f(2) = 2 + \sqrt{3} \)
同様に, \( g'(x) = \frac{\sqrt{x^2-1} – x}{\sqrt{x^2-1}} \)となり, こちらは\( f'(x) \)ほど符号は自明ではないが, 分母は正で, 分子の\( \sqrt{x^2-1} \)と\( x \)を比べると, 両辺正のときは\( \sqrt{x^2-1} < x \)である(両辺2乗すれば明らか)。
よって, \( g'(x) < 0 \)より, \( g(x) \leqq g(2) = 2 – \sqrt{3} \)
そのまま微分する場合
何も考えずに微分すると, おそらく, \( f'(t) = \frac{t-1}{2} \left( \frac{1}{t \sqrt{t}} + \frac{t+1}{t^2 \sqrt{t + \frac{1}{t} + 1}} \right) \)となり, 括弧の中は正なので, 増減表が書ける。
同様に, \( g'(t) \)も頑張って計算すると, \( g'(t) = \frac{t-1}{2} \left( \frac{\sqrt{t^2 + t + 1} – (t+1)}{t^2 \sqrt{t + \frac{1}{t} + 1}} \right) \)となり, \( t > 0 \)の範囲で括弧の中は常に負なので, 増減表が書ける。
計算ミスしなければこちらの方針でもOK。
(2)の下書き
三角形の成立条件は, \( a+b>c \)…①かつ\( b+c>a \)…②かつ\( c+a>b \)…③である。覚えていなくても, 簡単な三角形から連想すればよい(底辺の長さを5とすると, 残り2辺がの長さが2と3でギリギリ作れない, など)。
もし, 最大辺が仮に\( a \)だと判明している場合, \( a+b>c \)①と\( c+a>b \)③は当然成り立つので, \( b+c>a \)②だけを考えればよくなる。このように, 三角形の成立条件は, 辺の大小関係が分かると扱いやすくなる。
今回の場合, よくわからない\( p \)が入っている\( b = p\sqrt{xy} \)\( b \)は置いておいて, \( a = \sqrt{x^2 + xy + y^2} \)\( a \)と\( c = x + y \)\( c \)の長さを比べると,
$$\begin{eqnarray}
c^2 – a^2 &=& (x+y)^2 – (x^2+xy+y^2) \\
&=& xy > 0(\because x, y > 0)
\end{eqnarray}$$
より, \( c > a(\because a, c>0) \)
よって, \( a+b>c \)①, \( b+c>a \)②, \( c+a>b \)③のうち, \( b+c>a \)②は当然成り立つので, \( a+b>c \)①と\( c+a>b \)③だけを考えればよくなった。
まず\( a+b>c \)①を考えると, \( \sqrt{x^2 + xy + y^2} + p\sqrt{xy} > x + y \)。
これが任意の\( x, y \)で成り立つ\( p \)の条件を求めるので, \( p \)を定数分離してグラフを書くのが定石。\( \sqrt{xy} > 0 \)に注意して同値変形すると, \( p > \sqrt{\frac{x}{y}} + \sqrt{\frac{y}{x}} – \sqrt{\frac{x}{y} + 1 + \frac{y}{x}} \)となる。ここで(1)が使えそうなことに気づく。\( t = \frac{x}{y} \)と置くと, 右辺は\( g(t) \)そのものである。よって, \( p > g(t) \)が, 任意の\( t \)で成り立つように\( p \)を定めてやればよく, \( g(t) \)の最大値が\( 2 – \sqrt{3} \)だったから, \( p > 2 – \sqrt{3} \)…④であればよい。
同様に\( c+a>b \)③も考える。おそらく\( f(t) \)が出てくるのだろう。同様に式変形をすると, \( f(t) > p \)となる。これが任意の\( t \)で成り立つように\( p \)を定めてやると, \( f(t) \)の最小値が\( 2 + \sqrt{3} \)だったから, \( p < 2 + \sqrt{3} \)…⑤であればよい。
以上より, \( a+b>c \)①かつ\( c+a>b \)③の条件から求めた\( p > 2 – \sqrt{3} \)④かつ\( p < 2 + \sqrt{3} \)⑤が求める答えである。
実際の答案を書く際には, (1)を利用できる条件(\( t \)の範囲)を満たしていることを明示すること。
解答例
(1)\( \sqrt{t}, \frac{1}{\sqrt{t}}, t, \sqrt{t} \)はすべて正であるから, 相加相乗平均の大小関係より,
$$\begin{eqnarray}
f(t) \geqq 2\sqrt{\sqrt{t} \cdot \frac{1}{\sqrt{t}}} + \sqrt{2\sqrt{t \cdot \frac{1}{t}} + 1} = 2 + \sqrt{3}
\end{eqnarray}$$
である。実際に\( t = 1 \)のとき\( f(1) = 2 + \sqrt{3} \)となるので, \( f(t) \)の最小値は\( 2 + \sqrt{3} \)。
また,
$$\begin{eqnarray}
f(t)g(t) = \left( \sqrt{t} + \frac{1}{\sqrt{t}} \right)^2 – \left( \sqrt{t + \frac{1}{t} + 1} \right)^2 = 1
\end{eqnarray}$$
であり, \( f(t) > 0 \)であるから, \( g(t) > 0 \)である。
よって, \( g(t) = \frac{1}{f(t)} \)となり, \( f(t) \)が最小となるときに, \( g(t) \)は最大となる。
したがって, \( g(t) \)の最大値は, \( g(1) = \frac{1}{f(1)} = \frac{1}{2 + \sqrt{3}} = 2 – \sqrt{3} \)。
(2)\( x, y \)が正のとき, \( a, c \)も正であり, \( c^2 – a^2 = xy > 0 \)より, \( c>a \)。
よって, 三角形の成立条件は, \( c-a < b < c+a \)である。
\( t = \frac{x}{y}(>0) \)と置いて整理すると, \( g(t) < p < f(t) \)となる。
これが任意の\( t(>0) \)に関して成り立つには, \( p \)が\( g(t) \)の最大値より大きく, \( f(t) \)の最小値より小さければよいので, (1)より, 求める\( p \)の範囲は, \( 2 – \sqrt{3} < p < 2 + \sqrt{3} \)
振り返り
(1)も(2)も式を観察することの大切さを教えてくれる良問。(2)は三角形の成立条件を適用する箇所が若干難しいが, それ以外は標準的な難易度。
(2)では定数分離の結果, 自然と変数が減らせた(\( x, y \)の2変数から\( t \)の1変数へ)が, このような誘導がなくても, 同次式を見たら, 次数を減らせないか?と常に意識しておきたい。
なお, 最初から(2)が(1)の誘導であると気づく必要はない。(2)を解いている途中に気づけばよい。
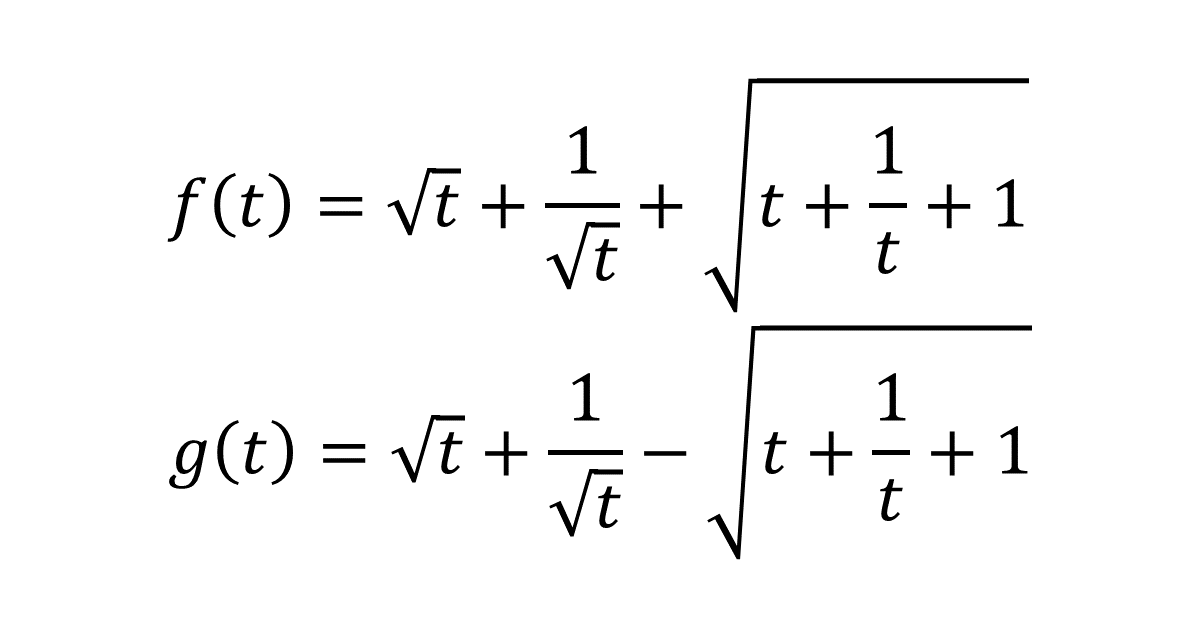
コメント