問題
数学的帰納法によって, \( \left( \displaystyle\frac{n+1}{2} \right)^n > n! \)を証明せよ。ここに\( n \)は\( 2 \)以上の整数とする。
発想
解法の指定があるのでそれに従う。
下書き
\( n=2 \)のときはすぐに示せるので省略。
\( n=k \)のときの\( ( \frac{k+1}{2} )^k > k! \)…①が成り立つことを仮定して, \( n=k+1 \)のときの\( ( \frac{k+2}{2} )^{k+1} > (k+1)! \)…②を示す。
\( ( \frac{k+2}{2} )^{k+1} > (k+1)! \)②を示すために, 引き算をする。\( ( \frac{k+1}{2} )^k > k! \)①を利用することを念頭に入れて, 少し分解してみる。
\begin{eqnarray}
\left( \frac{k+2}{2} \right)^{k+1} – (k+1)! &=& \left( \frac{k+2}{2} \right)^k \cdot \frac{k+2}{2} – (k+1) \cdot k! \\
\end{eqnarray}
\( k! \)が出てきたので, \( ( \frac{k+1}{2} )^k > k! \)①にマイナスを掛けたものを使って引き続き式変形していく。
(後で述べるように, この時点で見通しが付けば, マイナスの付いていない\( ( \frac{k+2}{2} )^{k+1} \)の方を変形するのがよい。)
\( ( \frac{k+1}{2} )^k > k! \)①より\( \color{red}{-k! > -( \frac{k+1}{2} )^k }\)を用いると,
\begin{eqnarray}
\left( \frac{k+2}{2} \right)^k \cdot \frac{k+2}{2} \color{red}{-} (k+1) \cdot \color{red}{k!}
&\color{red}{>}& \left( \frac{k+2}{2} \right)^k \cdot \frac{k+2}{2} \color{red}{-} (k+1) \cdot \color{red}{\left( \frac{k+1}{2} \right)^k} \\
\end{eqnarray}
帰納法の仮定(\( ( \frac{k+1}{2} )^k > k! \)①)も使い切ったので, あとはこの右辺だけに注目して\( 0 \)以上になることを示せばよい。
共通項(\( 2 \)の累乗)をくくると,
\begin{eqnarray}
\left( \frac{k+2}{2} \right)^k \cdot \frac{k+2}{2} – (k+1) \cdot \left( \frac{k+1}{2} \right)^k
&=& \frac{1}{2^{k+1}} \left\{ (k+2)^{k+1} – 2(k+1)^{k+1} \right\}
\end{eqnarray}
ここまでくると, 二項定理で展開するしかないことに気づくだろう。\( \color{red}{k+1} \)がたくさん出てくるので, それらをまとめることを考慮しながら,
\begin{eqnarray}
\frac{1}{2^{k+1}} \left\{ (k+2)^{k+1} – 2(k+1)^{k+1} \right\}
&=& \frac{1}{2^{k+1}} \left\{ \underline{(\color{red}{k+1} + 1)^{k+1}} – 2(\color{red}{k+1})^{k+1} \right\} \\
&=& \frac{1}{2^{k+1}} \left\{ \underline{\color{blue}{{}_{k+1}C_0 (k+1)^{k+1} + {}_{k+1}C_1 (k+1)^k} + {}_{k+1}C_2 (k+1)^{k-1} + \cdots + {}_{k+1}C_{k+1}} – 2(k+1)^{k+1} \right\} \\
&>& \frac{1}{2^{k+1}} \left\{ \color{blue}{(k+1)^{k+1} + (k+1)(k+1)^k} – 2(k+1)^{k+1} \right\} \\
&=& \frac{1}{2^{k+1}} \left\{ 2(k+1)^{k+1} – 2(k+1)^{k+1} \right\} \\
&=& 0
\end{eqnarray}
これで無事示せた。このように, 二項定理を使った不等式の証明では, 最初の二項だけで十分なことが多い(以下の解答例でも同様)。
また, 以下の解答例では, どうせ二項定理を使うのであればと, 最初の方に出てきた\( ( \frac{k+2}{2} )^{k+1} \)に対して二項定理を適用している。
解答例
\( ( \frac{n+1}{2} )^n > n! \)…①としておく。
(i) \( n=2 \)のとき, \( ( \frac{n+1}{2} )^n > n! \)①の左辺は\( \frac{9}{4} \), 右辺は\( 2 \)となるので, \( ( \frac{n+1}{2} )^n > n! \)①は成り立つ。
(ii) \( n=k \)のとき, \( ( \frac{n+1}{2} )^n > n! \)①が成り立つと仮定すると, \( \color{red}{( \frac{k+1}{2} )^k > k!} \)であるから,
\begin{eqnarray}
\left( \frac{(k+1)+1}{2} \right)^{k+1} – (k+1)! &=& \left( \frac{k+1}{2} + \frac{1}{2} \right)^k – (k+1)! \\
&=& \left( \frac{k+1}{2} \right)^{k+1} + _{k+1}C_{1}\left( \frac{k+1}{2} \right)^k \cdot \frac{1}{2} + _{k+1}C_{2}\left( \frac{k+1}{2} \right)^{k-1} \cdot \left\{ \frac{1}{2} \right\}^2 + \cdots + \left\{ \frac{1}{2} \right\}^{k+1} – (k+1)! \\
&>& \left( \frac{k+1}{2} \right)^{k+1} + \frac{k+1}{2} \cdot \left( \frac{k+1}{2} \right)^k – (k+1)! \\
&=& (k+1)\color{red}{\left( \frac{k+1}{2} \right)^k} – (k+1)! \\
&\color{red}{>}& (k+1)\color{red}{k!} – (k+1)! \\
&=& 0
\end{eqnarray}
よって, この仮定のもとで, \( n=k+1 \)のときも\( ( \frac{n+1}{2} )^n > n! \)①が成り立つ。
(i)(ii)より, \( 2 \)以上の自然数\( n \)に対して, \( ( \frac{n+1}{2} )^n > n! \)が成り立つ。
振り返り
二項定理を使う部分は, 慣れていないと思いつかないかもしれない。しかし, 解法の指定までしてあるので, 必ず正解しないといけない問題である。
補足
もし, 数学的帰納法に限定されていなかったら, どんな解法があるだろうか?以下に有力な手法を簡潔に紹介しておく。
まず, 微分は階乗があるので却下(微分可能の余地があるのは連続関数のみ)。
次に, 指数や階乗があれば, \( \log \)を取るのは自然であり, \( ( \frac{n+1}{2} )^n > n! \)①の右辺は
\begin{eqnarray}
\log n! = \log n + \log (n-1) + \cdots + \log 2
\end{eqnarray}
となる。この形は, 不等式評価で見たことがある人も多いはず。グラフの面積を考えて, 積分で評価をすることができる。(しかし本問の場合は, そこから先に進むのが難しい。)
また, 思いつきにくいが一番早いのは, 相加相乗平均を使う方法だろう。\( n \)項に拡張した相加相乗平均の大小関係
\begin{eqnarray}
\frac{1+2+\cdots+n}{n} \geqq \sqrt[n]{1 \times 2 \times \cdots \times n}
\end{eqnarray}
において, 左辺に等差数列の公式を使うと,
\begin{eqnarray}
\frac{\color{red}{1+2+\cdots+n}}{n} = \frac{1}{n} \cdot \color{red}{\frac{1}{2}n(n+1)} = \frac{n+1}{2}
\end{eqnarray}
となることに気付けば, ほぼ証明完了である。
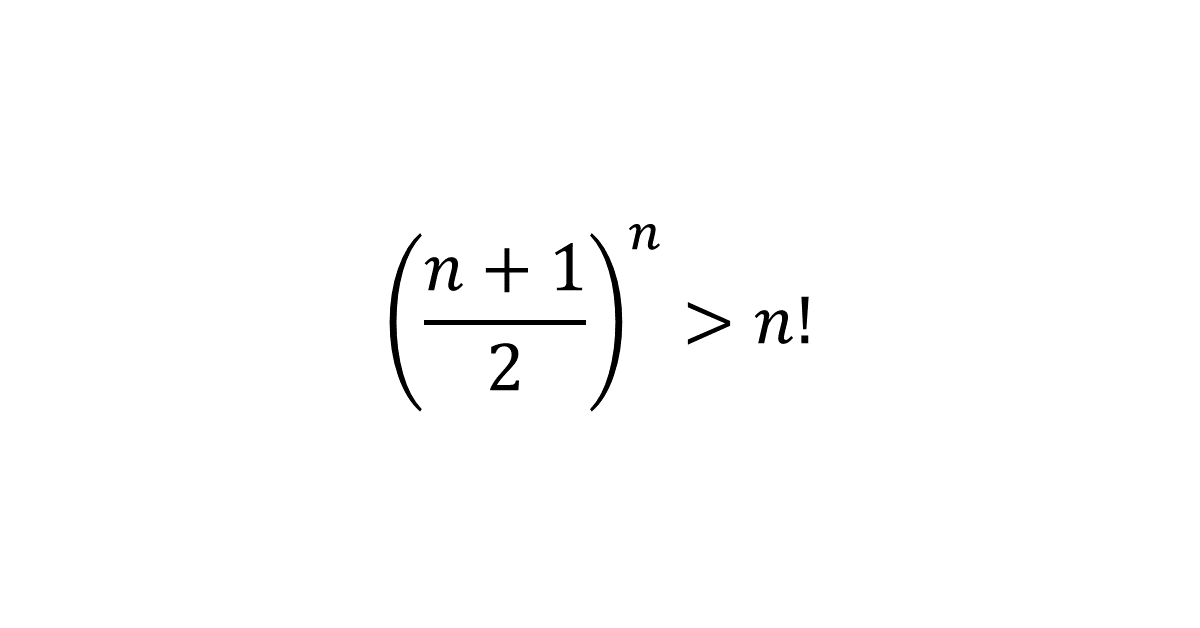
コメント