問題
\( p \)が素数であれば, どんな自然数\( n \)についても\( n^p – n \)は\( p \)で割り切れる。このことを, \( n \)についての数学的帰納法で証明せよ。
発想
解法の指定があるので, それに従う。
下書き
数学的帰納法で出来るか確認
(i) \( n = 1 \)のときは, \( 1^p – 1 = 0 \)は\( p \)で割り切れる。
(ii) \( n = k \)のとき, \( \color{red}{k^p – k} \)は\( p \)で割り切れると仮定する。
この仮定の下で, \( (\color{red}{k}+1)^\color{red}{p} \color{red}{-} (\color{red}{k}+1) \)は\( p \)で割り切れることを示す。
仮定を生かすことを考えると, \( (k+1)^p \)の部分に二項定理を使えば, \( \color{red}{k^p} \)の形が出てくる。
\begin{eqnarray}
\underline{(k+1)^p} – (k+1)
&=& \underline{{}_pC_0 k^p + {}_pC_1k^{p-1} + {}_pC_2k^{p-2} + \cdots + {}_pC_{p-2}k^2 + {}_pC_{p-1}k^1 + \require{cancel}\cancel{{}_pC_p}} – (k+\cancel{1}) \\
&=& \color{red}{k^p} + {}_pC_1k^{p-1} + {}_pC_2k^{p-2} + \cdots + {}_pC_{p-2}k^2 + {}_pC_{p-1}k \color{red}{- k} \\
&=& \color{red}{k^p – k} + \sum_{i=1}^{p-1}{}_pC_ik^{p-i}
\end{eqnarray}
ここで, 仮定より\( \color{red}{k^p – k} \)の部分は\( p \)で割り切れるので, あとは\( \displaystyle \sum_{i=1}^{p-1}{}_pC_ik^{p-i} \)の部分が\( p \)で割り切れる(\( p \)の倍数である)ことを示せばよい。
有名事実の利用
これは, 以下の有名事実を使う。
\( p \)が素数のとき, \( i = 1, 2, \cdots p-1 \)においては,
\( {}_pC_i \)は\( p \)の倍数
これは京大受験生には常識だが, 証明せずに使うと減点される可能性が高い。証明は一度理解すると簡単なので, 使うときは必ず証明とセットで使うこと。
この証明は, 以下の\(2\)点を言えばよいだろう。
\(1\)点目:\( {}_pC_i \)は整数。
\(2\)点目:\( {}_pC_i = \frac{\color{blue}{p}(p-1)\cdots(p-i+1)}{\color{red}{i}(\color{red}{i-1})\cdots\color{red}{2}\cdot1} \)の分母の各項(\( \color{red}{i} \)や\( \color{red}{i-1} \)や\( \color{red}{3} \)や\( \color{red}{2} \)など)は, 素数\( \color{blue}{p} \)と互いに素。
これら\(2\)点から, \( {}_pC_i \)は約分されて整数になるが, その際に\( p \)は残るので, \( p \)の倍数になるということが言える。この証明方法からもわかるように, 「\( p \)が素数」「\( i = 1, 2, \cdots p-1 \)」という条件は重要である。
解答例
まず, 「\( p \)が素数のとき, \( i = 1, 2, \cdots p-1 \)において, \( {}_pC_i \)は\( p \)の倍数である」…①を示しておく。
\( {}_pC_i = \frac{p(p-1)\cdots(p-i+1)}{i(i-1)\cdots2\cdot1} \)は, \( p \)個から\( i \)個を選ぶ組み合わせの数なので整数である。\( p \)は素数より, \( i, i-1, \cdots, 2 \)のそれぞれと互いに素だから約分されずに残り, \( {}_pC_i = p \times (整数) \)の形になるので, \( p \)が素数, \( i = 1, 2, \cdots p-1 \)のとき, \( {}_pC_i \)は\( p \)の倍数①は成り立つ。
次に, 任意の素数\( p \), 任意の自然数\( n \)に対して, \( n^p – n \)は\( p \)で割り切れることを, \( n \)に関する数学的帰納法で示す。
(i) \( n = 1 \)のときは, \( 1^p – 1 = 0 \)は\( p \)で割り切れる。
(ii) \( n = k \)のとき, \( k^p – k \)は\( p \)で割り切れる…②と仮定する。\( n=k+1 \)のとき,
\begin{eqnarray}
(k+1)^p – (k+1) &=& (省略)\\
&=& k^p – k + \displaystyle \sum_{i=1}^{p-1}{}_pC_ik^{p-i}…③
\end{eqnarray}
となる。
\( k^p – k \)は\( p \)で割り切れる②より\( k^p – k \)は\( p \)の倍数であり, \( p \)が素数, \( i = 1, 2, \cdots p-1 \)のとき, \( {}_pC_i \)は\( p \)の倍数①より\( \displaystyle \sum_{i=1}^{p-1}{}_pC_ik^{p-i} \)は\( p \)の倍数の和であるから, \( k^p – k + \displaystyle \sum_{i=1}^{p-1}{}_pC_ik^{p-i} \)③は\( p \)の倍数の和となる。すなわち, \( p \)で割り切れる。
(i)(ii)より, 題意は示された。
振り返り
完答しなければならないレベルの問題であるが, 差が付きやすい, いかにも京大らしい問題である。解き方は指定されていて一本道なので, \( {}_pC_i \)の性質を使う問題だと気づくことだけがポイント。\( {}_pC_i \)の性質は何度も出題されているので, 証明方法も含めて確実に理解しておかなければならない。
補足
フェルマーの小定理の紹介
本問は, 有名な「フェルマーの小定理」と関係している。
\( p \)が素数, \( n \)が\( p \)と互いに素な整数であるとき,
\( n^{p-1} \equiv 1 \pmod p \)
問題文は, フェルマーの小定理の合同式に\( n \)を掛けた, \( n^p \equiv n \pmod p \)と全く同じである。
実際, フェルマーの小定理の証明は, 本問でやったようにまず\( n^p \equiv n \pmod p \)を示してから, \( n \)と\( p \)が互いに素だから合同式の両辺を\( n \)で割って \( n^{p-1} \equiv 1 \pmod p \)と証明することが多い。
注意合同式の割り算が出来るのは, 互いに素のときだけ!
注意本問の表現(\( n^p \equiv n \pmod p \))の方が, 互いに素という前提が必要ないシンプルな形であり, こちらをフェルマーの小定理ということもある。
補題の紹介と証明
また, フェルマーの小定理には, もう一つの有名な証明方法が存在する。整数の剰余分類に関する, 以下の補題を用いる。
\( n \)と\( p \)が互いに素のとき, \( p-1 \)個の整数\( n, 2n, \cdots, (p-1)n \)を\( p \)で割った余りは, すべて異なる
証明は背理法で行う。等しい余りのものが存在すると仮定し, それらを \( kn, ln \) (ただし, \( \underline{1 \leqq k < l \leqq p-1} \))とする。「余りが等しい\( \Leftrightarrow \)差が割り切れる」の関係より, \( ln – kn = (\color{blue}{l-k})\color{red}{n} \)は\( p \)の倍数となる。ここで, \( \color{red}{n} \)は, \( p \)と互いに素だから, \( n \)は\( p \)の倍数ではない。一方, \( \color{blue}{l-k} \)も, \( \underline{1 \leqq k < l \leqq p-1} \)より \( 1 \leqq l-k \leqq p-2 \)だから, \( p \)の倍数にはなれない。よって矛盾する。
フェルマーの小定理の証明
補題①を用いて, フェルマーの小定理を証明する。
補題①は要するに, \( n \)と\( p \)が互いに素のとき, \( p-1 \)個の整数\( \color{red}{n}, \color{red}{2n}, \cdots, \color{red}{(p-1)n} \)を\( p \)で割った余りは, 順番は知らないが, \( p-1 \)通りの余り\( \color{blue}{1}, \color{blue}{2}, \cdots, \color{blue}{p-1} \)を(重複なく)全て尽くす, ということを言っている。
合同式を使えばここから直ちに,
\begin{eqnarray}
\color{red}{n} \times \color{red}{2n} \times \cdots \color{red}{(p-1)n} &\equiv& \color{blue}{1} \times \color{blue}{2} \times \cdots \times \color{blue}{(p-1)} \pmod p\\
&\Leftrightarrow&\\
n^{p-1}(p-1)! &\equiv& (p-1)! \pmod p
\end{eqnarray}
と書ける。ここに, \( p \)は素数という条件を追加すると, \( p \)と\( (p-1)! \)は互いに素となるので, 合同式でも割り算ができて, \( n^{p-1} \equiv 1 \pmod p \)が証明できる。
補足のまとめ
フェルマーの小定理は, 知らなくても全く問題ないが, 高校で習わない定理としては大学入試での活躍度がかなり高めなので, 知っていると得することがあるかもしれない。
補足の内容で一番重要なのは補題①の証明方法で, こちらは汎用性が高いので, 今後も似た証明を行う機会があるはずである。抽象的でわかりにくいかもしれないが, 是非理解しておくことをおすすめする。
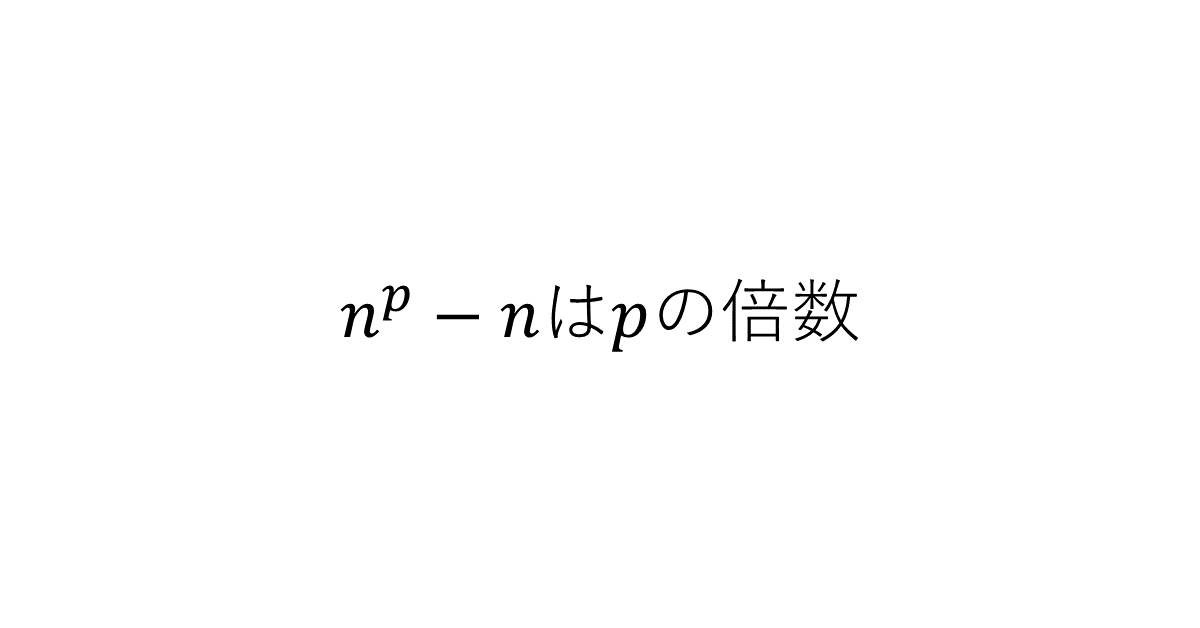
コメント