問題
\( a, b \)は\( a > b \)をみたす自然数とし, \( p, d \)は素数で\( p > 2 \)とする。このとき, \( a^p – b^p = d \)であるならば, \( d \)を\( 2p \)で割った余りが\( 1 \)であることを示せ。
発想
素数絡みだから, まずは因数分解を考える。結論は, 「\( d-1 \)が\( 2p \)で割り切れる」等に言い換えたほうが考えやすそう。
下書き
\( n \)乗の差の因数分解公式1を利用して,
\begin{eqnarray}
a^p – b^p = d \Leftrightarrow (a-b)(a^{p-1} + a^{p-2}b + \cdots + b^{p-1}) = d
\end{eqnarray}
よって, \( d \)は素数だから, 候補は以下の\(4\)通りに限定される。
| 候補\(1\) | 候補\(2\) | 候補\(3\) | 候補\(4\) | |
| \(a-b\) | \( 1 \) | \( d \) | \( -1 \) | \( -d \) |
| \(a^{p-1} + a^{p-2}b + \cdots + b^{p-1}\) | \( d \) | \( 1 \) | \( -d \) | \( -1 \) |
これらはもちろん絞り込めて, \(a^{p-1} + a^{p-2}b + \cdots + b^{p-1} > 0\)(または\( a > b \))より, マイナスの入った候補\(3,4\)は直ちに除外される。
また, \(a^{p-1} + a^{p-2}b + \cdots + b^{p-1} = 1 \)となることもなさそうなので, 候補\(1\)に確定。
よって, \(a-b=1\)…①と\(a^{p-1} + a^{p-2}b + \cdots + b^{p-1}=d\)…②が得られる。
\(a-b=1\)①という非常にシンプルな式が出てきたので, 文字を消去してみる。\(a^{p-1} + a^{p-2}b + \cdots + b^{p-1}=d\)②はややこしい式なので, シンプルな元の\( a^p – b^p = d \)の方に代入する。普通は\( b \)を消去するが, やってみるとマイナスが出てくるので, マイナスが出ないように\( a \)を消去してみる。
(むやみに式変形するのではなく, このように目的を持って, なるべくシンプルに式変形をする姿勢が大切)
\(a-b=1\)①より\( a = b+1 \)を\( a^p – b^p = d \)に代入して, \( (\color{red}{b}+1)^\color{red}{p} – \color{red}{b^p} = d \)…③
\( \color{red}{b^p} \)が消えてくれそうなので, 二項定理で展開するか, \( n \)乗の差の因数分解公式を使って整理する。
\begin{eqnarray}
\color{blue}{d} &=& \underline{(b+1)^p} – b^p \\
&=& \underline{{}_pC_0 b^p + {}_pC_1 b^{p-1} + {}_pC_2 b^{p-2} + \cdots + {}_pC_{p-1} b + {}_pC_p} – b^p \\
&=& \color{red}{b^p} + {}_pC_1 b^{p-1} + {}_pC_2 b^{p-2} + \cdots + {}_pC_{p-1} b + 1 – \color{red}{b^p} \\
&=& {}_pC_1 b^{p-1} + {}_pC_2 b^{p-2} + \cdots + {}_pC_{p-1} b + \color{blue}{1}
\end{eqnarray}
これで, \( \color{blue}{d – 1} \)が出てきた。
\( d-1 \)が\( p \)の倍数を示す
\( {}_pC_1b^{p-1} + {}_pC_2b^{p-2} + \cdots + {}_pC_{p-1}b \)の部分は\( p \)の倍数(京大受験生の常識。詳しくはこちら)なので, まず「\( d – 1 \)が\( p \)の倍数」と言える。
\( d-1 \)が\( 2 \)の倍数を示す
あとは, 「\( d-1 \)が\( 2 \)の倍数」ということを言いたい。少し扱いにくいので言い換えると, 「\( d-1 \)が偶数」, 「\( d \)が奇数」, などに言い換えられる。「\( d \)が奇数」がシンプルで良さそう。
\( d \)が出てくる式として, \(a^{p-1} + a^{p-2}b + \cdots + b^{p-1}=d\)②や\( (b+1)^{p} – b^p = d \)③があるが, どちらからでも「\( d \)が奇数」が言える。まずはシンプルな\( (b+1)^{p} – b^p = d \)③の利用を考える。
\( (b+1)^p – b^p = d \)…③を利用
まず前提として, 奇数は何乗しても奇数, 偶数は何乗しても偶数である。\( b+1 \)と\( b \)は連続する整数なので, 偶奇は異なる(一方が偶数なら, もう一方は奇数)。よって, \( (b+1)^p \)と\( b^p \)も偶奇は異なる。偶奇が異なるもの同士の引き算は, 必ず奇数になるので, \( (b+1)^{p} – b^p = d \)③より\( d \)は奇数。
\(a^{p-1} + a^{p-2}b + \cdots + b^{p-1}=d\)…②を利用
実はこちらの方が簡単。そもそも\( d \)は素数だから, \( d \)が\( 2 \)である可能性を排除できれば, 自動的に\( d \)は奇数となる。\(a^{p-1} + a^{p-2}b + \cdots + b^{p-1}=d\)②式よりほぼ明らかに\( d > 2 \)なので, \( d \)は奇数。
\( d-1 \)が\( 2p \)の倍数を示す
すでに\( d-1 \)が\( p \)の倍数, \( d-1 \)が\( 2 \)の倍数を示しているが, ここから直ちに\( d-1 \)は\( 2p \)の倍数, と書くと減点。\( p \)と\( 2 \)が互いに素ということを必ず断っておく。
(なぜこの一文が必要かわからない人は, 互いに素でないとどうなるか具体例で考えてみること)
解答例
\( a^p – b^p = d \)より,
$$(a-b)(a^{p-1} + a^{p-2}b + \cdots + b^{p-1}) = d$$
\( d \)は素数より,
$$(a-b, a^{p-1} + a^{p-2}b + \cdots + b^{p-1}) = (1, d), (d, 1), (-1, -d), (-d, -1)$$
ここで, \( a,b \)は自然数かつ\( p \geqq 3 \)より,
$$a^{p-1} + a^{p-2}b + \cdots + b^{p-1} \geqq 1 + 1 + 1 = 3$$
となるから,
$$(a-b, a^{p-1} + a^{p-2}b + \cdots + b^{p-1}) = (1, d)…①$$
となる。\( (a-b, a^{p-1} + a^{p-2}b + \cdots + b^{p-1}) = (1, d) \)①から得られる\( a-b = 1 \)を, \( a^p – b^p = d \)に代入して\( a \)を消去すると, \( (b+1)^p – b^p = d \)となる。
さらに展開して整理すると,
$${}_pC_1b^{p-1} + {}_pC_2b^{p-2} + \cdots + {}_pC_{p-1}b = d – 1…②$$
ここで, \( p \)が素数で, \( k = 1, 2, \cdots, p-1 \)のとき, \( {}_pC_k \)を考える。
\( {}_pC_k \)は整数で, \( {}_pC_k = \frac{p(p-1)\cdots(p-k+1)}{k(k-1) \cdots 2 \cdot 1} \)となるが, \( p \)は素数だから, 分子の\( p \)は, 分母の\( k, k-1, \cdots, 2 \)のそれぞれと約分されずに残る。よって, \( {}_pC_k \)は\( p \)の倍数である。
この事実を使うと, \( {}_pC_1b^{p-1} + {}_pC_2b^{p-2} + \cdots + {}_pC_{p-1}b = d – 1 \)②より, \( d-1 \)は\( p \)の倍数の和となるので, 「\( d-1 \)は\( p \)の倍数である」…③と言える。
また, \( (a-b, a^{p-1} + a^{p-2}b + \cdots + b^{p-1}) = (1, d) \)①から得られる\( a^{p-1} + a^{p-2}b + \cdots + b^{p-1} = d \)と, \( a,b \)は自然数かつ\( p \geqq 3 \)より,
\begin{eqnarray}
d &=& a^{p-1} + a^{p-2}b + \cdots + b^{p-1} \\
&\geqq& 1 + 1 + 1 = 3
\end{eqnarray}
となる。よって, \( d \)は\( 3 \)以上の素数, すなわち奇数である。
したがって, 「\( d-1 \)は\( 2 \)の倍数である」…④と言える。
\( d-1 \)は\( p \)の倍数③, \( d-1 \)は\( 2 \)の倍数④および, \( p \)は\( 3 \)以上の素数より\( p \)と\( 2 \)は互いに素であることから, \( d-1 \)は\( 2p \)の倍数である。
よって, \( d \)を\( 2p \)で割った余りは\( 1 \)である。
振り返り
京大過去問の中でもトップレベルの良問だが, 難易度は高い。\(a-b=1\)までは簡単なのでできてほしい。そのあとは, やみくもに式変形すると泥沼に陥る危険がある。使える式と結論をじっくりと見極めて, 出来るだけ簡単なものから活用する感覚を養いたい。
初見で解けなくても気にする必要はないので, 整数問題に必要な考え方をしっかり学び取ってほしい。
補足
\( a^p \)という形を見ると, フェルマーの小定理を思い浮かべる人もいるかもしれない。
\( p \)が素数, \( a \)が整数であるとき,
\( a^p \equiv a \pmod p \)
実際, 「\( d-1 \)が\( p \)の倍数」を示すところは, 以下のように, フェルマーの小定理を使うと簡単に示せる(本番でフェルマーの小定理を使いたい無謀な受験生は, 証明してから使うこと)。
\begin{eqnarray}
d &=& a^p – b^p (\because 与式) \\
&=& (b+1)^p – b^p (\because a=b+1) \\
&\equiv& (b+1) – b \pmod p (\because フェルマーの小定理) \\
&\equiv& 1 \pmod p
\end{eqnarray}
より, \( d \)を\( p \)で割った余りは\( 1 \)。
- 入試では知らないと解けない問題も意外と多いので, もし知らない, 覚えにくいという人は, \( x^3 – y^3 = (x-y)(x^2 + xy + y^2) \)の一般化にすぎないということを意識して, 確実に覚えておく。 ↩︎
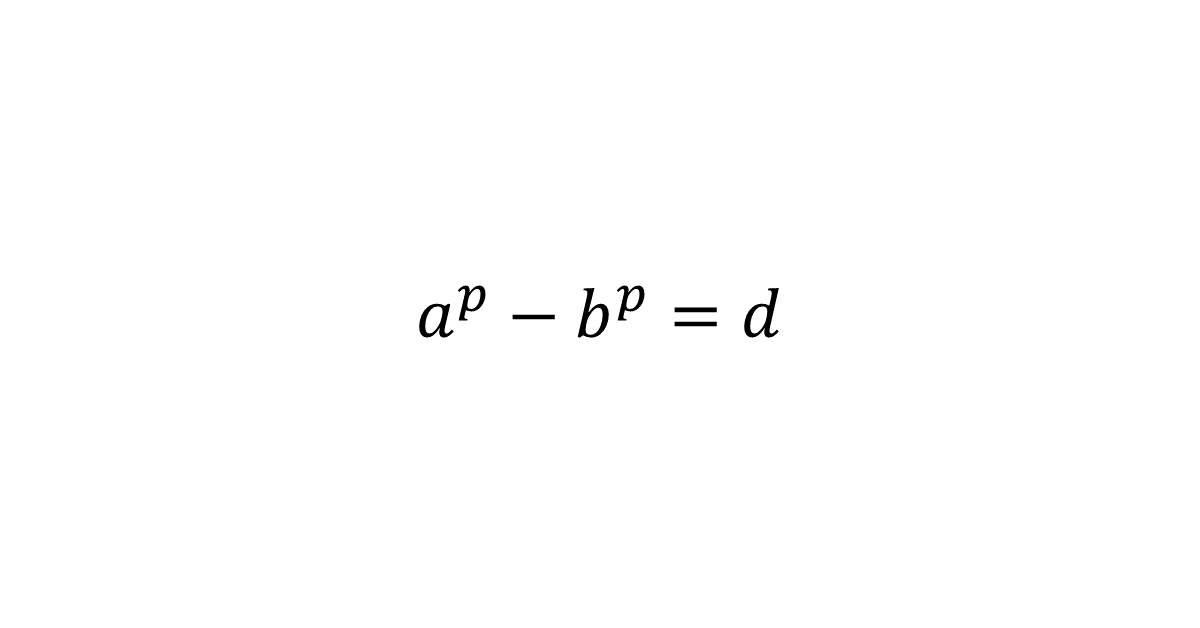
コメント