問題
以下の問に答えよ。ただし\( \sqrt{2}, \sqrt{3}, \sqrt{6} \)が無理数であることは使ってよい。
(1) 有理数\( p, q, r \)について, \( p + q\sqrt{2} + r\sqrt{3} = 0 \)ならば, \( p = q = r = 0 \)であることを示せ。
(2) 実数係数の\( 2 \)次式\( f(x) = x^2 + ax + b \)について, \( f(1), f(1 + \sqrt{2}), f(\sqrt{3}) \)のいずれかは無理数であることを示せ。
発想
(1)は, 類題「\( p + q\sqrt{2} = 0 \)ならば, \( p = q = 0 \)であることを示せ」をやったことがあるはずなので, 同様にできないか考える。
(2)は問題文から, 全て有理数と仮定して矛盾を導く方法が真っ先に思い浮かんでほしい。
あとはもちろん(1)の利用。まず素直に, 式変形で\( p + q\sqrt{2} + r\sqrt{3} = 0 \)の形に帰着させることが目標。「\( p + q\sqrt{2} + r\sqrt{3} + s\sqrt{6} = 0 \)ならば\( p = q = r = s = 0 \)」なども同様に示せそうなので, \( p + q\sqrt{2} + r\sqrt{3} + s\sqrt{6} = 0 \)などの形に帰着させるほうが楽かもしれない。実際に式変形をしてみないと分からない。
(1)の下書き
まず, 「\( p, q \)が有理数のとき, \( p + q\sqrt{2} = 0 \)ならば, \( p = q = 0 \)である」の示し方を確認しておく。
\( q \neq 0 \)と仮定すると, \( \sqrt{2} = -\frac{p}{q} \)と変形できるが, 左辺は無理数, 右辺は有理数となり, 矛盾。
よって仮定が間違っていて, \( q = 0 \)であることが分かり, そこから\( p = 0 \)も直ちに分かる。
このように背理法で簡単に示せる。これは京大受験生なら全員出来ないといけないので, 出来なかった人は今覚えること。
複素数の分野の「\( p, q \)が実数のとき, \( p + qi = 0 \)ならば, \( p = q = 0 \)である」や, ベクトルの分野の「\( \vec{a} \)と\( \vec{b} \)が一次独立のとき, \( p\vec{a} + q\vec{b} = \vec{0} \)ならば\( p = q = 0 \)である」という事実を何気なく使っている人も多いと思うが, ここでやったものと似ていると気付くだろうか。証明も同じようにできるので確認しておくと良い。
前者は, もし\( q \neq 0 \)とすると\( i = -\frac{p}{q} \)となるが, 左辺は虚数(虚部が\( 1 \)), 右辺は実数(虚部が\( 0 \))となるので矛盾。よって\( q = 0 \)で, \( p \)も\( 0 \)。
後者は, もし\( q \neq 0 \)とすると\( \vec{b} = -\frac{p}{q}\vec{a} \)となるが, これは\( \vec{a} \)と\( \vec{b} \)が一次独立ということに矛盾(一方が他方のスカラー倍になるのは一次独立ではない)。よって\( q = 0 \)で, \( p \)も\( 0 \)。
今回も, \( \sqrt{X} = (有理数) \)の形にして矛盾を導きたいので, 根号を一つにするために, 適当に\( 2 \)乗してやればよい。\( q\sqrt{2} \)でも\( r\sqrt{3} \)でもどちらでもよいが, 例えば\( q\sqrt{2} \)を移項した\( p + r\sqrt{3} = -q\sqrt{2} \)を\( 2 \)乗すると, \( \color{red}{2}\sqrt{3}\color{red}{pq} = 2q^2 – p^2 – 3r^2 \)となるので, 上と同様にやると, \( \color{red}{2pq} = 0 \)となる。あとは\( p = 0 \)の場合と\( q = 0 \)で場合分けすれば示せるはず。
(2)の下書き
いずれかが無理数であることを示すのは難しいので, 背理法で, 「全て有理数」と仮定して矛盾を導く。
・\( f(1) = a + b + 1 = \frac{n_1}{m_1} \)(\( m_1 \)は自然数, \( n_1 \)は整数, \( n_1 \)と\( m_1 \)は互いに素)
・\( f(1 + \sqrt{2}) = (1 + \sqrt{2})a + b + 3 + 2\sqrt{2} = \frac{n_2}{m_2} \)(同上)
・\( f(\sqrt{3}) = \sqrt{3}a + b + 3 = \frac{n_3}{m_3} \)(同上)
のように置くのが自然。ここからの変形はよく考える必要がある。
この3つの式を使って, \( p + q\sqrt{2} + r\sqrt{3} = 0 \)のような形にしたいが, (1)で示した通り, \( p, q, r \)は有理数である。
ここで, \( a, b \)は有理数とも無理数ともいわれていない, よくわからない文字なので, いわば邪魔な文字。よって, \( a, b \)を消去するのが正解。
3つの式から\( a, b \)を消去する。
よく見ると, \( b \)の係数はすべて\( 1 \)なので, 辺々引き算すると\( b \)は簡単に消える。よって, まず\( a \)だけの式が2つ出てくる。あとは, その2つの式から\( a \)を消去すればOK。
3分くらい頑張って計算すると,
\( \frac{n_3}{m_3} – \frac{n_1}{m_1} + 2 + (\frac{n_1}{m_1} – \frac{n_2}{m_2} + 2)\sqrt{2} + (\frac{n_3}{m_3} – \frac{n_1}{m_1} – 2)\sqrt{3} = 0 \)
となるので, (1)より,
・\( \color{red}{\frac{n_3}{m_3} – \frac{n_1}{m_1}} + 2 = 0 \)…①
・\( \frac{n_1}{m_1} – \frac{n_2}{m_2} + 2 = 0 \)
・\( \color{red}{\frac{n_3}{m_3} – \frac{n_1}{m_1}} – 2 = 0 \)…②
となる。しかし, ①と②は明らかに矛盾している(同時には成り立たない)ので, 結局仮定が間違っていることが示せて, 終了。
式変形をやってみると, \( \frac{n_1}{m_1} \)などはまとめて考えていることが分かると思うので, \( = \frac{n_1}{m_1} \)(\( m_1 \)は自然数, \( n_1 \)は整数, \( n_1 \)と\( m_1 \)は互いに素)などと置かなくても, \( = m_1 \)(\( m_1 \)は有理数)などと置けば十分であることが分かる。
解答例
(1)
まず, 「有理数\( r_1, r_2 \)および\( n = 2, 3, 6 \)について, \( r_1 + r_2\sqrt{n} = 0 \)ならば, \( r_1 = r_2 = 0 \)」…①を示しておく。
もし, \( r_2 \neq 0 \)なら, \( r_1 + r_2\sqrt{n} = 0 \)より, \( \sqrt{n} = -\frac{r_1}{r_2} \)と変形できる。
このとき, 左辺は無理数であり, 右辺は有理数となるから, 矛盾が生じる。
よって, \( r_2 = 0 \)であり, \( r_1 + r_2\sqrt{n} = 0 \)より, \( r_1 = 0 \)であるので, \( r_1 + r_2\sqrt{n} = 0 \)ならば, \( r_1 = r_2 = 0 \)①は成り立つ。
\( p + q\sqrt{2} + r\sqrt{3} = 0 \)…②のとき, \( p + r\sqrt{3} = -q\sqrt{2} \)であり, 両辺を\( 2 \)乗して整理すると, \( 2q^2 – p^2 – 3r^2 – 2pq\sqrt{3} = 0 \)となる。
\( 2q^2 – p^2 – 3r^2, -2pq \)は有理数だから, \( r_1 + r_2\sqrt{n} = 0 \)ならば, \( r_1 = r_2 = 0 \)①より, \( -2pq = 0 \), すなわち\( p = 0 \)または\( q = 0 \)である。
(i) \( p = 0 \)のとき, \( p + q\sqrt{2} + r\sqrt{3} = 0 \)②は, \( q\sqrt{2} + r\sqrt{3} = 0 \)となり, 両辺を\( \sqrt{2} \)倍すると, \( 2q + r\sqrt{6} = 0 \)となる。
よって, \( 2q, r \)は有理数だから, \( r_1 + r_2\sqrt{n} = 0 \)ならば, \( r_1 = r_2 = 0 \)①より, \( q = r = 0 \)である。
(ii) \( q = 0 \)のとき, \( p + q\sqrt{2} + r\sqrt{3} = 0 \)②は, \( p + r\sqrt{3} = 0 \)となる。
よって, \( p, r \)は有理数だから, \( r_1 + r_2\sqrt{n} = 0 \)ならば, \( r_1 = r_2 = 0 \)①より, \( p = r = 0 \)である。
(2)
\( f(1), f(1 + \sqrt{2}), f(\sqrt{3}) \)が全て有理数と仮定する。このとき,
\( f(1) = a + b + 1 = r_3 \)…③
\( f(1 + \sqrt{2}) = (1 + \sqrt{2})a + b + 3 + 2\sqrt{2} = r_4 \)…④
\( f(\sqrt{3}) = \sqrt{3}a + b + 3 = r_5 \)…⑤
と置ける(\( r_3, r_4, r_5 \)は有理数)。
③④より\( b \)を消去すると, \( \sqrt{2}a + 2 + 2\sqrt{2} = r_4 – r_3 \)…⑥
③⑤より\( b \)を消去すると, \( (\sqrt{3} – 1)a + 2 = r_5 – r_3 \)…⑦
⑥⑦より\( a \)を消去して整理すると,
\( r_5 – r_3 + 2 + (r_3 – r_4 + 2)\sqrt{2} + (r_5 – r_3 – 2)\sqrt{3} = 0 \)
\( r_5 – r_3 + 2, r_3 – r_4 + 2, r_5 – r_3 – 2 \)は有理数だから, (1)より, \( r_5 – r_3 + 2 = r_5 – r_3 – 2 = 0 \)となるが, これは, \( 2 = -2 \)となり矛盾。
よって, \( f(1), f(1 + \sqrt{2}), f(\sqrt{3}) \)のいずれかは無理数である。
振り返り
(1)は完答しないといけない。落ち着いて場合分けをしてすべての場合を尽くせばOK。
(2)も難しくはないが, 式変形で沼にはまる可能性がある。式がごちゃごちゃになったら, 一旦元の式に戻ることが大切。今回の場合は, 3つの式から, 文字を2つ消去して, 1つの式にする, という構造が分かっていれば, そこまで迷うことはないはずである。\( \sqrt{6} \)が出てきて困った!と言う人は, 解答の\( (\sqrt{3} – 1)a + 2 = r_5 – r_3 \)⑦式に\( (\sqrt{3} – 1) \)が入っていることに着目し, \( (\sqrt{3} – 1)a + 2 = r_5 – r_3 \)⑦式を\( a = \)のように書いて有理化してから, \( \sqrt{2}a + 2 + 2\sqrt{2} = r_4 – r_3 \)⑥式に代入すればよい。
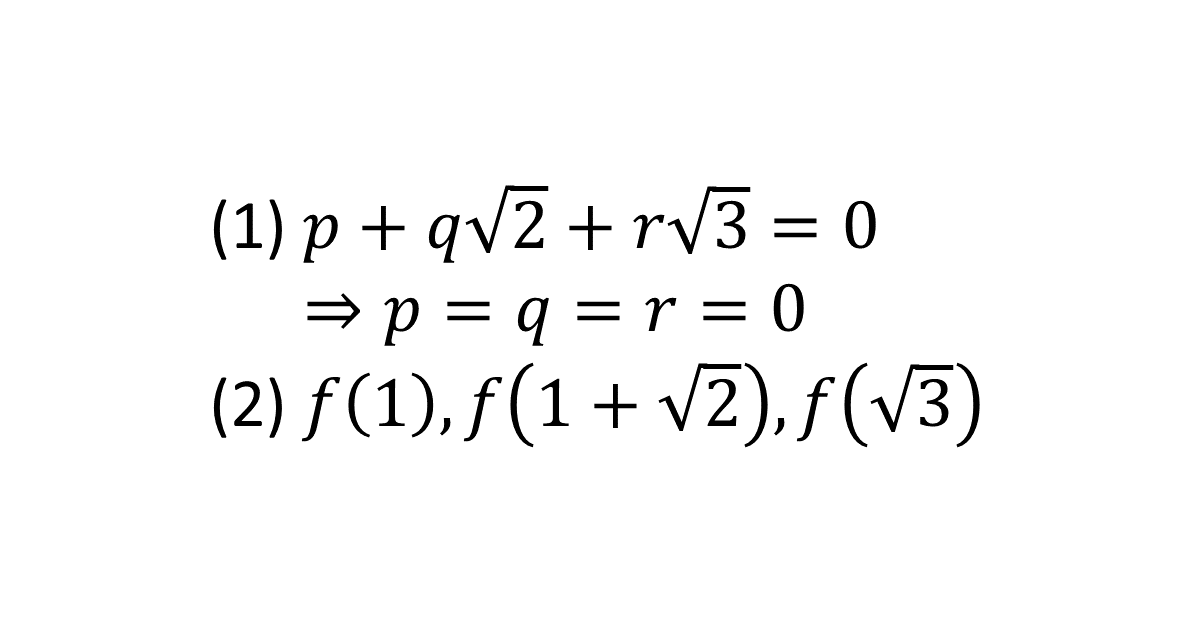
コメント