問題
整数\( n \)に対し\( f(n) = \frac{n(n-1)}{2} \)とおき, \( a_n = i^{f(n)} \)と定める。ただし, \( i \)は虚数単位を表す。このとき, \( a_{n+k} = a_n \)が任意の整数\( n \)に対して成り立つような正の整数\( k \)をすべて求めよ。
発想
まずは実験して周期を予想する。等式があるので, 等式を変形することから始めてもよい。
下書き
解法1:実験から考える
| \( n \) | \( \cdots \) | \( 1 \) | \( 2 \) | \( 3 \) | \( 4 \) | \( 5 \) | \( 6 \) | \( 7 \) | \( 8 \) | \( 9 \) | \( 10 \) | \( \cdots \) |
| \( f(n) \) | \( \cdots \) | \( 0 \) | \( 1 \) | \( 3 \) | \( 6 \) | \( 10 \) | \( 15 \) | \( 21 \) | \( 28 \) | \( 36 \) | \( 45 \) | \( \cdots \) |
| \( i^{f(n)} \) | \( \cdots \) | \( 1 \) | \( i \) | \( -i \) | \( -1 \) | \( -1 \) | \( -i \) | \( i \) | \( 1 \) | \( 1 \) | \( i \) | \( \cdots \) |
\( 1, i, -i, -1, -1, -i, i, 1 \)の\( 8 \)周期だと予測できるので, \( a_n = a_{n+8} = a_{n+16} = \cdots \)が成り立ちそう。よって, \( f(n+8) \)と\( f(n) \)の関係を調べてみる。
$$\begin{eqnarray}
f(n+8) – f(n) &=& \frac{(n+8)(n+7)}{2} – \frac{n(n-1)}{2}\\
&=& \frac{(n^2 + 15n + 56) – (n^2 – n)}{2} \\
&=& \frac{16n+56}{2} \\
&=& 8n+28 \\
&=& 4(2n+7)
\end{eqnarray}$$
よって, \( f(n+8) = f(n) + 4(2n+7) \)だから,
$$\begin{eqnarray}
a_{n+8} &=& i^{f(n+8)} = i^{f(n) + 4(2n+7)}\\
&=& i^{f(n)} \cdot \color{red}{i^{4(2n+7)}} = a_{n} \cdot \color{red}{1} \\
&=& a_{n}
\end{eqnarray}$$
ここで, \( i^4 \)は\( 1 \)なので, \( \color{red}{i^{4m}} \) (\( m \)は整数)も\( \color{red}{1} \)であることを用いた。
これで\( a_{n+8} = a_n \)となったので, \( a_n \)の周期が\( 8 \)であることが証明できて, 終了。
解答例のように, 周期が\( 8 \)より小さいことはないということはきちんと記述しておかないといけない。
また正の整数\( k \)をすべて求めよとあるので, \( k=8 \)だけでなく, \( k \)は\( 8 \)の倍数, のように答えないといけないことにも注意。
解法2:式変形から考える
\( a_{n+k} = a_n \)を変形していく。
$$\begin{eqnarray}
a_{n+k} = a_n &\Leftrightarrow& i^{f(n+k)} = i^{f(n)}\\
&\Leftrightarrow& \frac{i^{f(n+k)}}{i^{f(n)}} = 1\\
&\Leftrightarrow& i^{f(n+k)-f(n)} = 1
\end{eqnarray}$$
\( i \)を\( f(n+k)-f(n) \)乗すると\( 1 \)になるのだから, \( f(n+k)-f(n) \)は\( 4 \)の倍数。\( f(n+k)-f(n) \)を計算すると,
$$\begin{eqnarray}
f(n+k)-f(n) &=& \frac{(n+k)(n+k-1)}{2} – \frac{n(n-1)}{2} \\
&=& \frac{\{ n^2 + (2k-1)n + k(k-1) \} – \{ n^2 – n \}}{2} \\
&=& \frac{1}{2}\{ 2kn + k(k-1) \} \\
&=& \frac{1}{2}k(2n + k – 1)
\end{eqnarray}$$
より, これが\( 4 \)の倍数ということは, \( k(2n+k-1) \)が\( 8 \)の倍数。
これが任意の\( n \)について成り立つような\( k \)を求める。これは, 必要条件から攻める方法が自然に思いついてほしい。
・\( n = 0 \)で成り立つことが必要なので, \( k(k-1) \)が\( 8 \)の倍数であることが必要。
・\( n = 1 \)で成り立つことも必要なので, \( k(k+1) \)が\( 8 \)の倍数であることも必要。
・\( n = 2 \)で成り立つことも必要なので, \( k(k+3) \)が\( 8 \)の倍数であることも必要。
\( \cdots \)
これらの条件を見ると, \( k \)が\( 8 \)の倍数であることが必要そうであることがわかる。よって, まずは必要条件として\( k \)が\( 8 \)の倍数であることを示しにいく。
\( k(k-1) \)が\( 8 \)の倍数\( \cdots ① \)かつ\( k(k+1) \)が\( 8 \)の倍数\( \cdots ② \)の2つの条件から, \( k \)が\( 8 \)の倍数を示す。
「連続整数は互いに素」に着目
\( k(k-1) \)が\( 8 \)の倍数①は, \( 8 \)の約数である\( 1,2,4,8 \)が, \( k \)および\( k-1 \)にどのように分配されるかを教えてくれる。考えられるのは, 「\( k-1 \)が\( 8 \)の倍数」「\( k \)が\( 2 \)の倍数で\( k-1 \)が\( 4 \)の倍数」「\( k \)が\( 4 \)の倍数で\( k-1 \)が\( 2 \)の倍数」「\( k \)が\( 8 \)の倍数」の4通り。ここで, 連続する整数は互いに素という常識を思い出すと, 「\( k-1 \)が\( 8 \)の倍数」「\( k \)が\( 8 \)の倍数」の2通りに絞られる。
つまり, \( k(k-1) \)が\( 8 \)の倍数①から, \( k \)か\( k-1 \)のどちらかが\( 8 \)の倍数と言える。
同様に, \( k(k+1) \)が\( 8 \)の倍数②から, \( k \)か\( k+1 \)のどちらかが\( 8 \)の倍数と言える。
\( k-1 \)と\( k+1 \)が同時に\( 8 \)の倍数となることはないので, \( k \)が\( 8 \)の倍数と確定する。
よって, 少なくとも\( k \)が\( 8 \)の倍数であることが必要である。
「偶奇」に着目
\( k(k-1) \)が\( 8 \)の倍数①と\( k(k+1) \)が\( 8 \)の倍数②を使って, \( k \)の偶奇に着目しても, \( k \)が\( 8 \)の倍数と言うことができる。
(i) もし\( k \)が偶数なら, \( k-1 \)は奇数だから, \( k(k-1) \)が\( 8 \)の倍数①より\( k \)の方が\( 8 \)の倍数となるしかないのでOK。
(ii) もし\( k \)が奇数なら, \( k(k-1) \)が\( 8 \)の倍数①より\( k-1 \)の方が\( 8 \)の倍数となるしかない。同じように\( k(k+1) \)が\( 8 \)の倍数②を考えると, \( k+1 \)の方が\( 8 \)の倍数となるしかない。ここで, \( k-1 \)と\( k+1 \)がともに\( 8 \)の倍数となることはあり得ないので, そもそも\( k \)は奇数ではなかった。
(i)(ii)より, \( k \)が\( 8 \)の倍数であることが必要である。
いずれにせよこれで必要条件が分かったので, 十分性を確認すればよい。つまり, 逆に, \( k \)が\( 8 \)の倍数のとき, \( k(2n+k-1) \)は明らかに\( 8 \)の倍数となる。
解答例1
任意の整数\( n \)について,
$$\begin{eqnarray}
f(n+8) &=& \frac{(n+8)(n+7)}{2}\\
&=& \frac{n(n-1)}{2} + 8n+28\\
&=& f(n) + 4(2n+7)
\end{eqnarray}$$
よって,
$$\begin{eqnarray}
a_{n+8} &=& i^{f(n+8)} = i^{f(n) + 4(2n+7)}\\
&=& i^{f(n)} \cdot i^{4(2n+7)} = a_{n} (\because nは整数)
\end{eqnarray}$$
したがって\( a_n \)は\( 8 \)個ごとに同じ値が現れる。
一方, \( a_1 \)から\( a_8 \)の値は以下のとおりであるから, \( 8 \)より小さい正の整数\( k \)で, \( a_{n+k} = a_n \)が成り立つことはない。
| \( a_1 \) | \( a_2 \) | \( a_3 \) | \( a_4 \) | \( a_5 \) | \( a_6 \) | \( a_7 \) | \( a_8 \) |
| \( 1 \) | \( i \) | \( -i \) | \( -1 \) | \( -1 \) | \( -i \) | \( i \) | \( 1 \) |
以上より, \( a_n \)は周期が\( 8 \)と分かるので, 求める\( k \)は, \( 0 \)より大きい\( 8 \)の倍数すべてである。
解答例2
\( f(n+k)-f(n) = \frac{1}{2}k(2n + k – 1) \)だから,
$$\begin{eqnarray}
a_{n+k} = a_n &\Leftrightarrow& i^{f(n+k)} = i^{f(n)}\\
&\Leftrightarrow& i^{f(n+k)-f(n)} = 1\\
&\Leftrightarrow& \frac{1}{2}k(2n + k – 1)が4の倍数\\
&\Leftrightarrow& k(2n + k – 1)が8の倍数
\end{eqnarray}$$
これが任意の\( n \)について成り立つような正の整数\( k \)を求める。
まず, \( n=0 \)のときを考えて, \( k(k-1) \)が\( 8 \)の倍数であることが必要である。\( k \)と\( k-1 \)は互いに素だから, \( k \)と\( k-1 \)のどちらか一方が\( 8 \)の倍数となる。
次に, \( n=1 \)のときを考えて, \( k(k+1) \)が\( 8 \)の倍数であることが必要である。同様に\( k \)と\( k+1 \)のどちらか一方が\( 8 \)の倍数となる。
ここで, \( k-1 \)と\( k+1 \)がともに\( 8 \)の倍数となることはないので, \( k \)が\( 8 \)の倍数となることが必要である。
逆に\( k \)が\( 8 \)の倍数であるとき, 任意の整数\( n \)について\( k(2n + k – 1) \)は\( 8 \)の倍数である。
以上より, 求める正の整数\( k \)は, すべての\( 8 \)の倍数である。
振り返り
実験すれば簡単に予測でき, それを示すのも難しくない。
式変形で示す方は, 後半部分が多少難しく, 整数問題に慣れていないと厳しいかもしれない。しかし, 必要条件から考える, という全体の方針は必ず理解しておくこと。
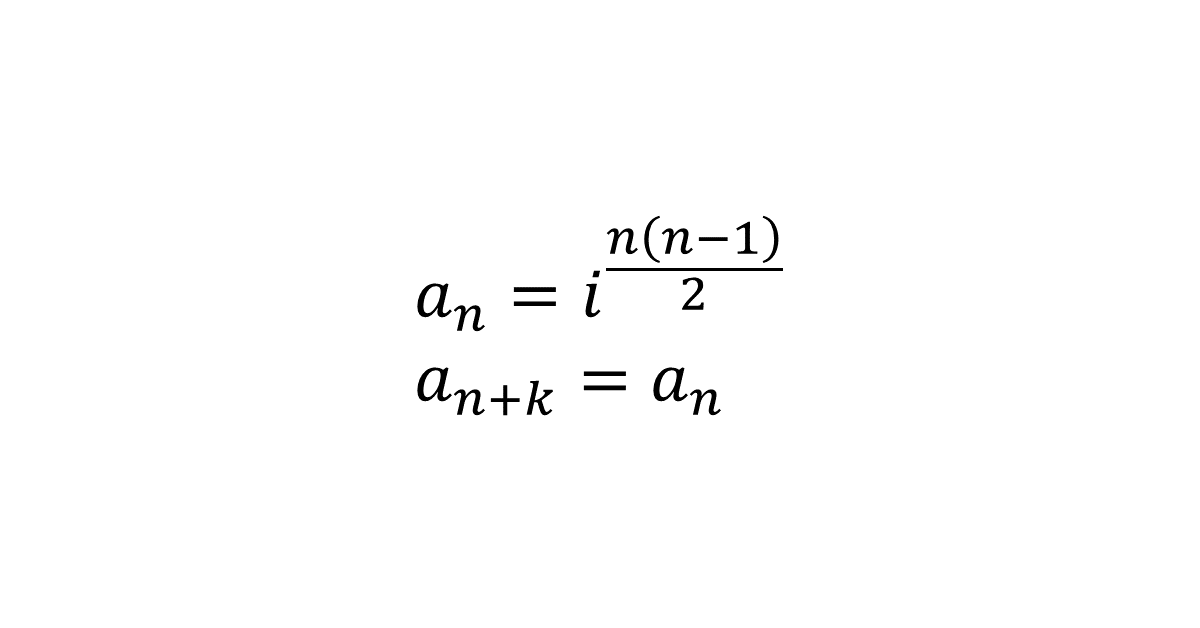
コメント