問題
\( n \)を自然数とする。次の3つの不等式(1), (2), (3)をすべて満たす自然数の組\( (a, b, c, d) \)はいくつあるか。\( n \)を用いてあらわせ。
(1) \( 1 \leqq a < d \leqq n \)
(2) \( a \leqq b < d \)
(3) \( a < c \leqq d \)
発想
文字が多いので, まずは実験して雰囲気をつかむ。
下書き
小さい\( n \)で実験する。\( n = 1 \)では\( 1 \leqq a < d \leqq n \)(1)を満たす\( a, d \)が存在しないので, \( n = 2 \)から始める。
\( n = 2 \)のとき
\( 1 \leqq a < d \leqq n \)(1)は\( 1 \leqq a < d \leqq 2 \)となり, \( (a, d) = (1, 2) \)と確定。
このとき, \( a \leqq b < d \)(2)は\( 1 \leqq b < 2 \), \( a < c \leqq d \)(3)は\( 1 < c \leqq 2 \)となり, \( (b, c) = (1, 2) \)と確定。
よって, 1通り。
\( n = 3 \)のとき
\( 1 \leqq a < d \leqq n \)(1)は\( 1 \leqq a < d \leqq 3 \)となり, \( (a, d) = (1, 2), (2, 3), (1, 3) \)の3通り。
(i) \( (a, d) = (1, 2) \)のとき, 先ほどとまったく同様に, \( (b, c) = (1, 2) \)と確定する。
(ii) \( (a, d) = (2, 3) \)のとき, 先ほどとほとんど同じで, \( (b, c) = (2, 3) \)と確定する。
(iii) \( (a, d) = (1, 3) \)のとき, \( a \leqq b < d \)(2)は\( 1 \leqq b < 3 \), \( a < c \leqq d \)(3)は\( 1 < c \leqq 3 \)となり, \( b, c \)はそれぞれ2通り取りうるので, \( (b, c) \)の組は\( 2 \times 2 = 4 \)通り。
(i)(ii)(iii)より, \( 1 + 1 + 4 = 6 \)通り。
\( n = 4 \)のとき
\( 1 \leqq a < d \leqq n \)(1)は\( 1 \leqq a < d \leqq 4 \)となり, \( (a, d) = (1, 2) \), \( (2, 3) \), \( (3, 4) \), \( (1, 3) \), \( (2, 4) \), \( (1, 4) \)の6通り。
ここまでの実験で,
\( (a, d) = (1, 2), (2, 3), (3, 4) \)のように差が1のときは, \( (b, c) \)は\( \color{red}{1} \)つに確定する。
\( (a, d) = (1, 3), (2, 4) \)のように差が2のときは, \( (b, c) \)の組は\( \color{blue}{4} \)つある。
ということがわかる。
\( (a, d) = (1, 4) \)のときは, \( a \leqq b < d \)(2)は\( 1 \leqq b < 4 \), \( a < c \leqq d \)(3)は\( 1 < c \leqq 4 \)となり, \( b, c \)はそれぞれ3通り取りうるので, \( (b, c) \)の組は\( 3 \times 3 = 9 \)通り。
よって, \( 3 \times \color{red}{1} + 2 \times \color{blue}{4} + 1 \times 9 = 20 \)通り。
\( n = n \)のとき(一般の場合)
ここまでで, だいたいつかめたので, 一般の\( n \)の場合を考えてみる(不安な場合は, \( n = 5 \)の場合も考えてみること)。
\( 1 \leqq a < d \leqq n \)(1)は\( 1 \leqq a < d \leqq n \)であり, まず\( (a, d) \)の組は, \( a, b \)の差に注意して分けると, 以下の通り。
\( (a, d) = (1, 2), (2, 3), \cdots, (n-1, n) \)…①
\( (a, d) = (1, 3), (2, 4), \cdots, (n-2, n) \)…②
\( \cdots \)
\( (a, d) = (1, 1 + k), (2, 2 + k), \cdots, (n-k, n) \)…③
\( \cdots \)
\( (a, d) = (1, n) \)…④
ここで, \( k \)を使って一般化した\( (a, d) = (1, 1 + k), (2, 2 + k), \cdots, (n-k, n) \)③を途中に書いた。
この\( k \)は, \( (a, d) = (1, 2), (2, 3), \cdots, (n-1, n) \)①や\( (a, d) = (1, n) \)④と見比べることにより, \( k = 1, 2, \cdots, n-1 \)を取ることが分かる。
次に, それぞれの場合について, \( (a, d) \)の組の数を求める。
\( (a, d) = (1, 2), (2, 3), \cdots, (n-1, n) \)①のとき, \( (a, d) \)の組を数えると\( \color{red}{n-1} \)通りある。
\( (a, d) \)それぞれの組について, \( d = a+1 \)だから, \( a \leqq b < d \)(2)は\( a \leqq b < a+1 \), \( a < c \leqq d \)(3)は\( a < c \leqq a+1 \)となり, \( b, c \)はそれぞれ1通りしかとらない。
よって, 組\( (a, b, c, d) \)は, \( (\color{red}{n-1}) \times \color{blue}{1} \times \color{blue}{1} = n-1 \)通り。
\( (a, d) = (1, 3), (2, 4), \cdots, (n-2, n) \)②のとき, \( (a, d) \)の組を数えると\( \color{red}{n-2} \)通りある。
\( (a, d) \)それぞれの組について, \( d = a+2 \)だから, \( a \leqq b < d \)(2)は\( a \leqq b < a+2 \), \( a < c \leqq d \)(3)は\( a < c \leqq a+2 \)となり, \( b, c \)はそれぞれ2通りずつ取りうる。
よって, 組\( (a, b, c, d) \)は, \( (\color{red}{n-2}) \times \color{blue}{2} \times \color{blue}{2} = 4(n-2) \)通り。
\( (a, d) = (1, 1 + k), (2, 2 + k), \cdots, (n-k, n) \)③は後回しにして\( (a, d) = (1, n) \)④のとき, \( (a, d) \)の組を数えると(もちろん)\( \color{red}{1} \)通りある。
このとき, \( a \leqq b < d \)(2)は\( 1 \leqq b < n \), \( a < c \leqq d \)(3)は\( 1 < c \leqq n \)となり, \( b, c \)はそれぞれ\( n-1 \)通りずつ取りうる。
よって, 組\( (a, b, c, d) \)は, \( \color{red}{1} \times (\color{blue}{n-1}) \times (\color{blue}{n-1}) = (n-1)^2 \)通り。
このようにして, 各場合分けに対して個数を求め, それぞれを足し合わせれば完了。
つまり, 一般化した\( (a, d) = (1, 1 + k), (2, 2 + k), \cdots, (n-k, n) \)③の場合の個数を求め, \( k = 1, 2, \cdots, n-1 \)で足し合わせればよい。
計算は特に難しくないが, 必ず検算すること。
解答例
\( 1 \leqq a < d \leqq n \)(1)より, \( (a, d) \)の組は,
\( (a, d) = (1, 1 + k), (2, 2 + k), \cdots, (n – k, n) ( k = 1, 2, \cdots, n-1 ) \)
となる。このとき, 各\( k \)に対して, \( (a, b, c, d) \)の組を数える。
まず, \( (a, d) \)の組は, \( n – k \)通りある。
次に, \( a \leqq b < d \)(2)は\( l \leqq b < l + k \)(\( l = 1, 2, \cdots, n – k \))となるので, \( b \)は, \( b = l, l+1, \cdots, l + k – 1 \)の\( k \)通りをとりうる。
最後に, \( a < c \leqq d \)(3)は\( l < c \leqq l + k \)(\( l = 1, 2, \cdots, n – k \))となるので, \( c \)は, \( c = l+1, l+2, \cdots, l + k \)の\( k \)通りをとりうる。
よって, この\( k \)のとき, \( (a, b, c, d) \)の組は, \( (n-k) \cdot k \cdot k = k^2(n-k) \)通りである。
したがって, 求める場合の数は,
$$\begin{eqnarray}
\sum_{k=1}^{n-1} k^2(n-k) &=& n\sum_{k=1}^{n-1} k^2 – \sum_{k=1}^{n-1} k^3 \\
&=& n \cdot \frac{1}{6}(n-1)n\left\{ 2(n-1) + 1 \right\} – \left\{ \frac{1}{2}(n-1)n \right\}^2 \\
&=& \frac{1}{12}n^2(n-1)\left\{ 2(2n-1) – 3(n-1) \right\} \\
&=& \frac{1}{12}n^2(n^2-1)
\end{eqnarray}$$
振り返り
文字ばかりで一見とっつきづらいが, 実験すると単純な不等式だと分かる。解答例のように一般化すると綺麗に書けるが, いきなり書けるはずもないので, 納得するまで実験をすることが大切。
一般化した書き方に慣れている人には簡単で, 慣れていない人は解き方は何となく分かっても書きづらかったと思われる。京大は, 抽象的な問題(例えば一般の\( n \)を使った問題)が好きなので, 一般化して解答を書き上げる練習を普段からしておく必要がある。
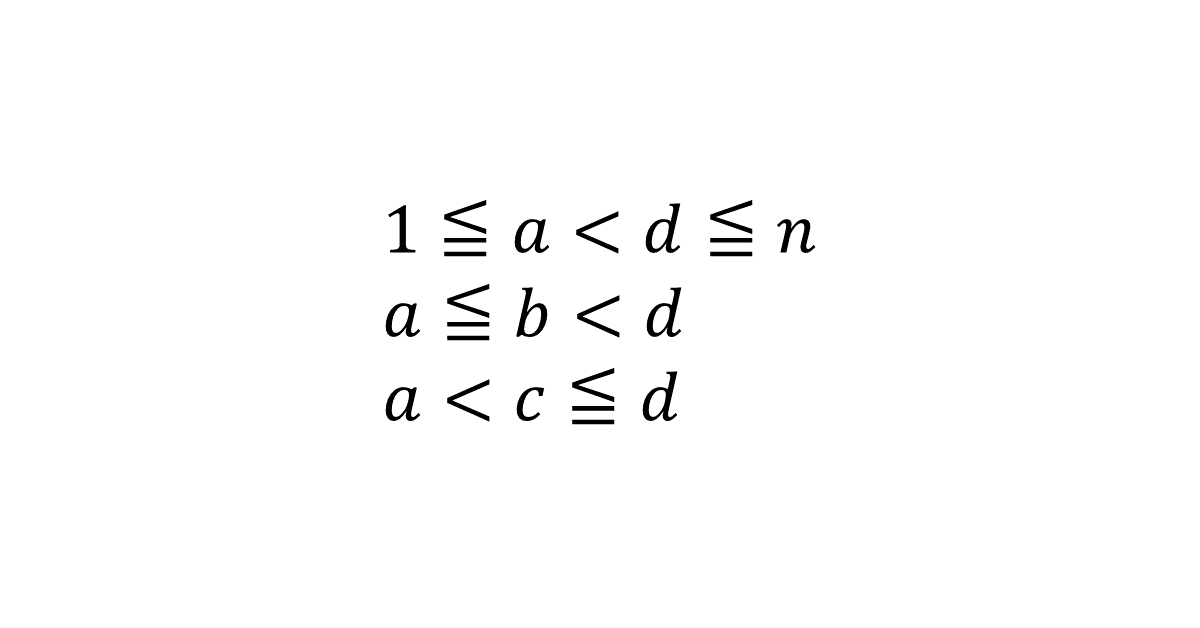
コメント