問題
\( n \)個のボールを\( 2n \)個の箱へ投げ入れる。各ボールはいずれかの箱に入るものとし, どの箱に入る確率も等しいとする。どの箱にも\(1\)個以下のボールしか入っていない確率を\( p_n \)とする。このとき, 極限値\( \displaystyle \lim_{n \to \infty} \frac{\log p_n}{n} \)を求めよ。
発想
\( p_n \)は, 変に考えずに, 直接求めることができる。
\( \frac{\log p_n}{n} \)の部分は, いろんな式変形が考えられるので, ここがポイント。
下書き
\( p_n \)を求める
\( p_n \)は, ボールの視点に立つと,
\(1\)個目のボールはどこに入ってもよい。
\(2\)個目のボールは, 残り\( 2n – 1 \)個のどれかに入るので, 確率は\( \frac{2n-1}{2n} \)。
\(3\)個目のボールは, 残り\( 2n – 2 \)個のどれかに入るので, 確率は\( \frac{2n-2}{2n} \)。
\( \cdots \)
\(n\)個目のボールは, 残り\( 2n – (n-1) \)個のどれかに入るので, 確率は\( \frac{2n-(n-1)}{2n} \)。
よって, \( p_n = \frac{2n-1}{2n} \times \frac{2n-2}{2n} \times \cdots \times \frac{2n-(n-1)}{2n} \)。
\( p_n \)の別の求め方
もしくは, 場合の数的に考えて, 全事象の場合の数と, 該当事象の場合の数の比から, \( p_n \)を求めてもよい。
今回, 全事象の数は, \( (2n)^n \)。
該当事象(どの箱にも\(1\)個以下のボールしか入らない事象)の数は, \( {}_{2n}\mathrm{P}_n \)(注意\( {}_{2n}\mathrm{C}_n \)ではない)。
よって, \( p_n = \frac{{}_{2n}\mathrm{P}_n}{(2n)^n} = \frac{(2n)!}{n!(2n)^n} \)。
極限を求められるように式変形
いずれにせよ, ここから, \( \displaystyle\lim_{n \to \infty} \frac{\log p_n}{n} \)が求められるように変形していく。\(\text{log}\)内部の掛け算は足し算になることや, \( \displaystyle\lim_{n \to \infty}\frac{1}{n} \)があることなどから, 区分求積っぽいという感性が働くのが望ましい。区分求積だと分かれば, 前者の\( p_n \)を使って以下のようにやるのが早いだろう。
\begin{eqnarray}
\lim_{n \to \infty} \frac{\log \color{red}{p_n}}{n}
&=& \lim_{n \to \infty} \frac{1}{n} \log \left( \color{red}{\frac{2n-1}{2n} \times \frac{2n-2}{2n} \times \cdots \times \frac{2n-(n-1)}{2n}} \right) \\
&=& \lim_{n \to \infty} \frac{1}{n} \left\{ \log \left( 1-\frac{1}{2n} \right) + \log \left( 1-\frac{2}{2n} \right) + \cdots + \log \left( 1-\frac{n-1}{2n} \right) \right\} \\
&=& \lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^{n-1} \log \left( 1-\frac{k}{2n} \right) \\
&=& \int_0^1 \log \left( 1 – \frac{x}{2} \right) dx
\end{eqnarray}
あとは適当に積分して終了。
解答例は, あえてわかりやすさより綺麗さを重視した答案とした。
ここまでの内容が理解できた人は, 細かい式変形を追う必要はない。
意欲のある人は, 総和記号(\( \sum \))や総乗記号(\( \prod \))1を展開して, 式変形が正しいことを確認してみてほしい。
解答例
どの箱にも\(1\)個以下のボールしか入らないとき, \( k \)番目(\( k=1,2, \cdots, n \))のボールが空の箱に入る確率は\( \frac{2n-(k-1)}{2n} \)だから,
\begin{eqnarray}
\color{red}{p_n} = \displaystyle\prod_{k=1}^n \frac{2n-(k-1)}{2n} = \color{red}{\displaystyle\prod_{k=1}^{n-1} \left(1-\frac{k}{2n}\right)}
\end{eqnarray}
よって,
\begin{eqnarray}
\lim_{n \to \infty} \frac{\log \color{red}{p_n}}{n}
&=& \lim_{n \to \infty} \frac{1}{n} \log \color{red}{\prod_{k=1}^{n-1} \left(1-\frac{k}{2n}\right)}\\
&=& \lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^{n-1} \log \left( 1-\frac{k}{2n} \right)\\
&=& \int_0^1 \log \left( 1 – \frac{x}{2} \right) dx \\
&=& \color{red}{\int_0^1} \{ \color{red}{\log (2-x)} – \log 2 \}\color{red}{dx} \\
&=& \color{red}{\Big[ x \log (2-x) \Big]_0^1 + \int_0^1 \underline{\frac{x}{2-x}} dx} – \log2 \\
&=& 0 + \int_0^1(\underline{-1 -\frac{2}{x-2}})dx – \log2 \\
&=& \Big[ -x -2 \log |x-2| \Big]_0^1 – \log2 \\
&=& \log2 – 1
\end{eqnarray}
振り返り
\( p_n \)を求めるところは簡単。その後, 区分求積に持っていく思考と, 式変形が若干難しい。区分求積が思いつかなければおしまいなので, 区分求積のヒントを察知することが大切である。また, \( p_n \)を階乗や累乗でまとめてしまうと, 区分求積が見えずらいので, 式変形もポイントである。
分かってしまえばなんてことない問題だが, 実際の出来はかなり悪かったと思われる。解けたら周りと差をつけられるような問題である。
- 何故か高校では習わないが, 総和記号の掛け算バージョンというだけである。例えば, \( \displaystyle\prod_{k=1}^{n} a_k = a_1 \times a_2 \times \cdots \times a_n \) ↩︎
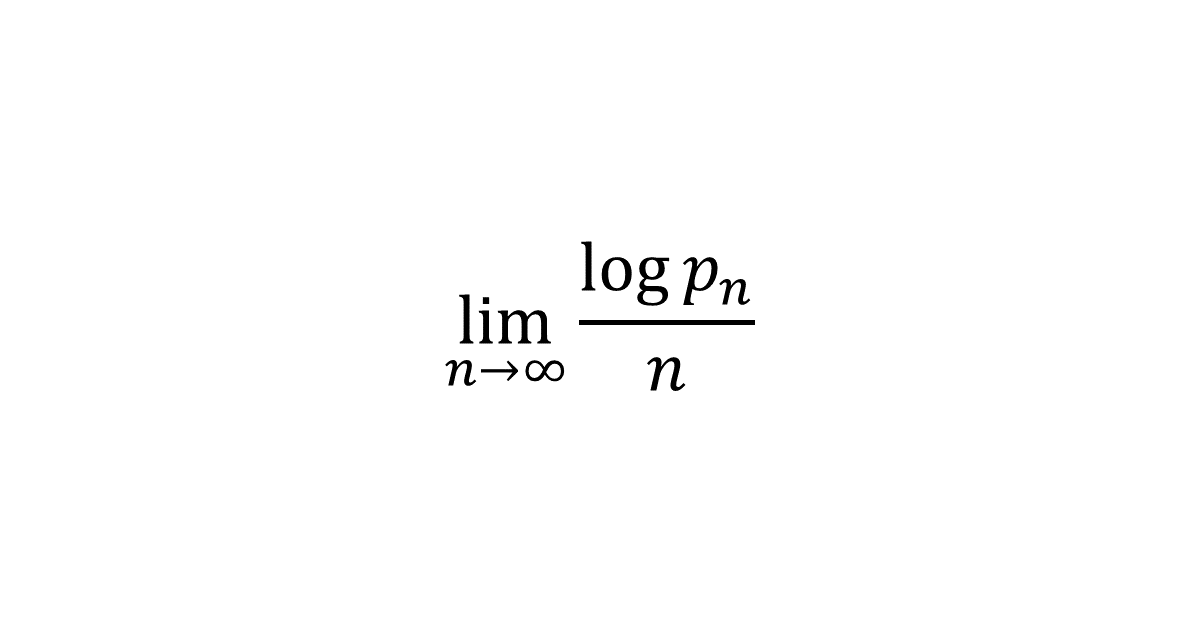
コメント