問題
\( \{a_n\} \)を正の数からなる数列とし, \( p \)を正の実数とする。このとき\( a_{n+1} > \frac{1}{2}a_n – p \)をみたす番号\( n \)が存在することを証明せよ。
発想
数列があるので, 不等号を等号と見なして普通に変形すると\( a_{n+1} + 2p > \frac{1}{2}(a_n + 2p) \)となる。しかし, 通常の数列は, \( a_{n+1} + 2p = \frac{1}{2}(a_n + 2p) \)がすべての\( n \)について成り立つので, ここからさらに\( a_n + 2p = (\frac{1}{2})^{n-1}(a_1 + 2p) \)という変形ができた。
今回は, \( a_{n+1} + 2p > \frac{1}{2}(a_n + 2p) \)となる\( n \)が(何か一つでも)あることを示す問題なので, 全ての\( n \)についてはもちろん成り立っていない。よって, 問題文に\( a_{n+1} > \frac{1}{2}a_n – p \)と書いてあるからと言って, いつもの調子でいきなり\( a_n + 2p > (\frac{1}{2})^{n-1}(a_1 + 2p) \)と変形するのは致命的な間違いである。
すべての\( n \)で成り立つ条件を使いたいので, 背理法で否定してみる。
注意\(n\)に関する命題を\( P(n) \)とすると, 「ある\(n\)について\( P(n) \)が成り立つ」の否定は, 「すべての\(n\)について\( P(n) \)が成り立たない」である。
下書き
\( a_{n+1} + 2p > \frac{1}{2}(a_n + 2p) \)をみたす番号\( n \)が存在しないと仮定すると, すべての\( n \)について, \( a_{n+1} + 2p \leqq \frac{1}{2}(a_n + 2p) \)が成り立つ。
よって, この式の\( n \)を\( n-1, n-2, \cdots \)にしたものを順に適用することによって,
\( a_n + 2p \leqq \frac{1}{2}(\color{red}{a_{n-1} + 2p}) \color{red}{\leqq} \frac{1}{2} \cdot \color{red}{\frac{1}{2}(a_{n-2} + 2p)} \leqq \cdots \leqq (\frac{1}{2})^{n-1}(a_1 + 2p) \)
となる(普通の数列と同じように変形できる)。
さて, ここから矛盾を導くことになるが, ほぼ自明に, \( n \)が大きくなれば不等式\( a_n + 2p \leqq (\frac{1}{2})^{n-1}(a_1 + 2p) \)は成り立たなくなり, 矛盾と言える。
たとえば, \( n = 10000 \)では, \( a_{10000} + 2p \leqq (\frac{1}{2})^{9999}(a_1 + 2p) \)となるが, 右辺は限りなくゼロに近く, 左辺は正なので, 矛盾。
もし\( n = 10000 \)でも, まだ\( a_{10000} + 2p > (\frac{1}{2})^{9999}(a_1 + 2p) \)が成り立っていれば, もっと大きい\( n \)を代入すればよい。
この辺りの論理は厳密に書くことは難しいが, 高校範囲でしっかり習うこともないので, 適当に\( n \to \infty \)のとき…と書いておけば十分である。
解答例
\( a_{n+1} > \frac{1}{2}a_n – p \)をみたす番号\( n \)が存在しないと仮定すると, すべての\( n \)で\( a_{n+1} \leqq \frac{1}{2}a_n – p \)が成り立つ。
よって, \( a_n + 2p \leqq (\frac{1}{2})^{n-1}(a_1 + 2p) \)と変形できる。
条件より, 左辺は常に正である。
ここで, \( n \to \infty \)とすると, (右辺)\( \to 0 \)となるが, これは(左辺)\( > 0 \)に矛盾する。
したがって, \( a_{n+1} > \frac{1}{2}a_n – p \)をみたす番号\( n \)は存在する。
振り返り
抽象的で一見とっつきにくいが, やってみると意外と簡単で, 合否の分かれ目になる問題。
与えられた数列の不等式を利用するためには, 背理法がうまくはまると気づくことが最大のポイントである。
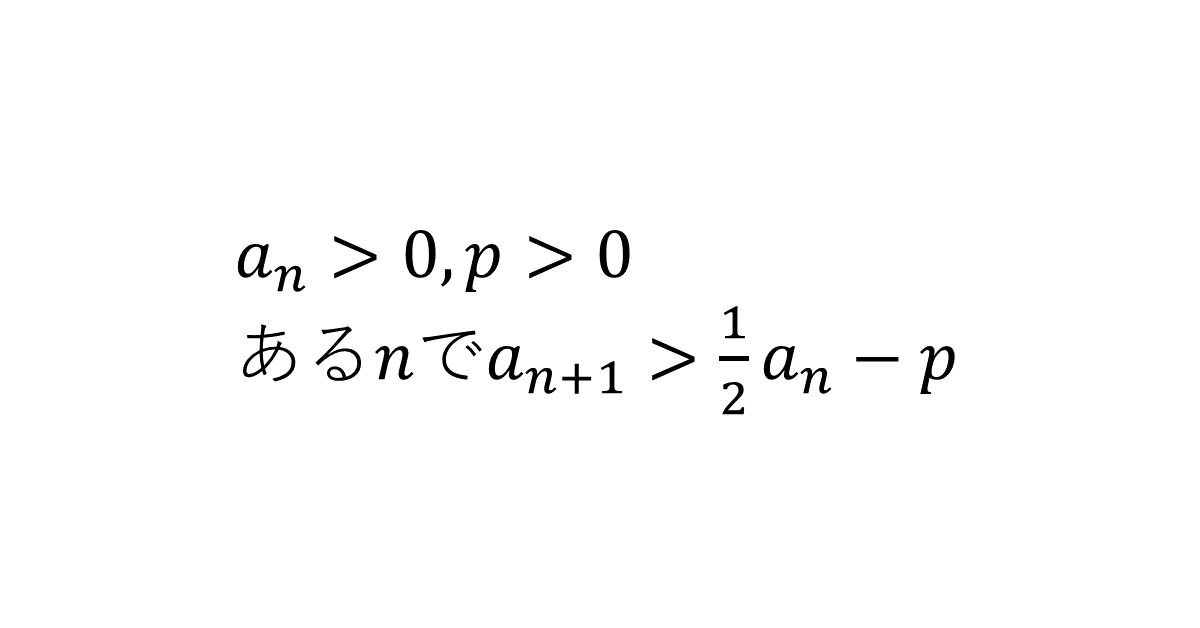
コメント