問題
数列\( \{a_n\} \)は, すべての正の整数\( n \)に対して\( 0 \leqq 3a_n \leqq \displaystyle\sum_{k=1}^n a_k \)を満たしているとする。このとき, すべての\( n \)に対して\( a_n=0 \)であることを示せ。
発想
\( n \)に関する証明なので数学的帰納法は真っ先に思いつくが, あまり見ない設定なので, 具体的に書きながら性質を調べてみる。
下書き
「すべての正の整数\( n \)に対して\( 0 \leqq 3a_n \leqq \displaystyle\sum_{k=1}^n a_k \)」というのは, 常に成り立つ前提。よって,
・\( n=1 \)のときの, \( 0 \leqq 3a_1 \leqq a_1 \)…①
・\( n=2 \)のときの, \( 0 \leqq 3a_2 \leqq a_1 + a_2 \)…②
・\( n=3 \)のときの, \( 0 \leqq 3a_3 \leqq a_1 + a_2 + a_3 \)…③
\( \cdots \)
これらはすべて, いつでもどこでも使ってよい。
順に見ていくと, まず\( 0 \leqq 3a_1 \leqq a_1 \)①より, \( a_1 = 0 \)が成り立つ。
これを\( 0 \leqq 3a_2 \leqq a_1 + a_2 \)②に代入すると, \( 0 \leqq 3a_2 \leqq a_2 \)となり, 同様に\( a_2 = 0 \)が成り立つ。
これらを\( 0 \leqq 3a_3 \leqq a_1 + a_2 + a_3 \)③に代入すると, \( 0 \leqq 3a_3 \leqq a_3 \)となり, 同様に\( a_3 = 0 \)が成り立つ。
…
このように順番に, すべて\( 0 \)と言うことができるので, 帰納法で示せそうである。
注意点は, \( a_3 = 0 \)を言うときに, \( a_1 = 0 \)と\( a_2 = 0 \)のどちらも代入している。よって, 帰納法の仮定は, 前ひとつではなく, 前すべてを仮定しないといけない。
解答例
(i) \( n = 1 \)のとき, \( 0 \leqq 3a_n \leqq \displaystyle\sum_{k=1}^n a_k \)に\( n=1 \)を代入して, \( 0 \leqq 3a_1 \leqq a_1 \)。
よって, \( 0 \leqq a_1 \)かつ\( a_1 \leqq 0 \)より, \( a_1 = 0 \)が成り立つ。
(ii) \( n=1, 2, \cdots, k \)のとき, \( a_1=0, a_2=0, \cdots, a_k=0 \)…①が成り立つと仮定する。
このとき, \( 0 \leqq 3a_n \leqq \displaystyle\sum_{k=1}^n a_k \)に\( n=k+1 \)を代入して, \( 0 \leqq 3a_{k+1} \leqq a_1 + \cdots + a_k + a_{k+1} \)。
\( a_1=0, a_2=0, \cdots, a_k=0 \)①を代入すると, \( 0 \leqq 3a_{k+1} \leqq a_{k+1} \)。
よって, \( 0 \leqq a_{k+1} \)かつ\( a_{k+1} \leqq 0 \)より, \( a_{k+1} = 0 \)が成り立つ。
(i)(ii)より, すべての\( n \)に対して\( a_n=0 \)が成り立つ。
振り返り
数学的帰納法をきちんと理解していますかというだけの, 非常に簡単な問題。しかし, 数学的帰納法に慣れていないと, 自分でも何を書いているかわからなくなったり, 論理展開が合っているかどうか不安になるかもしれない。今はどの仮定が使えて, どの結論を言おうとしているのか, はっきりと意識することが大切である。本問を使って, 数学的帰納法の基本的な考え方を確実に身に付けてほしい。
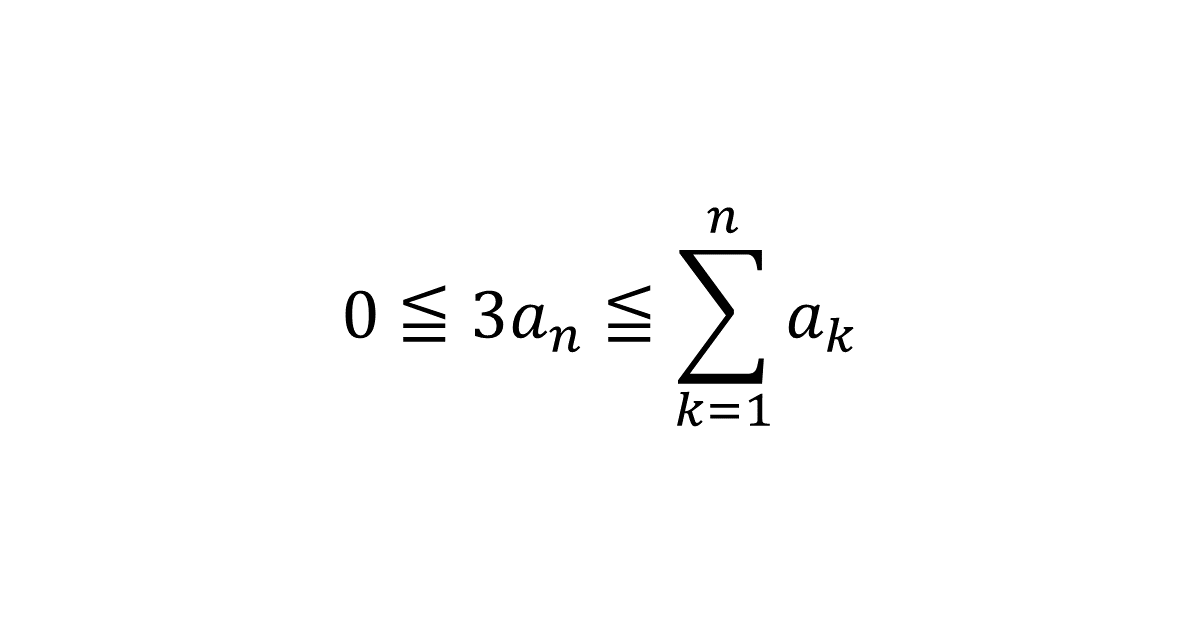
コメント