問題
\( xy \)平面上に\( 2n \)個の点\( A_i(i, 1), B_i(i, 2) \)(\( i=1, 2, \cdots, n \))がある。上下に隣り合う\( 2 \)点\( A_i, B_i \)を結ぶ線分を「縦辺」(\( i=1, 2, \cdots, n \)), 左右に隣り合う\( 2 \)点\( A_i, A_{i+1} \)および\( B_i, B_{i+1} \)を結ぶ線分を「横辺」(\( i=1, 2, \cdots, n-1 \))と言う。すべての横辺には, 各辺独立に, 確率\( p \)で右向きの矢印が, 確率\( 1-p \)で×印が描かれている。またすべての縦辺には常に上向きの矢印が描かれている。このとき点\( A_1(1, 1) \)から出発して, 矢印の描かれている辺だけを通り, 矢印の方向に進んで, 点\( B_n(n, 2) \)に到達する経路が少なくとも\( 1 \)本存在する確率を\( Q_n \)とする。以下の問に答えよ。
(1) \( Q_2, Q_3 \)を求めよ。
(2) \( Q_n \)を求めよ。
発想
誘導があるので, 小さい\( n \)ではしらみつぶしに実験してから, 一般の\( n \)にどうつなげるのかを考える。
下書き
\( Q_2 \)
\( n=2 \)のときの図は正方形になる。横辺は2つあり, それぞれ矢印か×の2通りなので, \( 2^2 = 4 \)通りを調べればよいだけ。
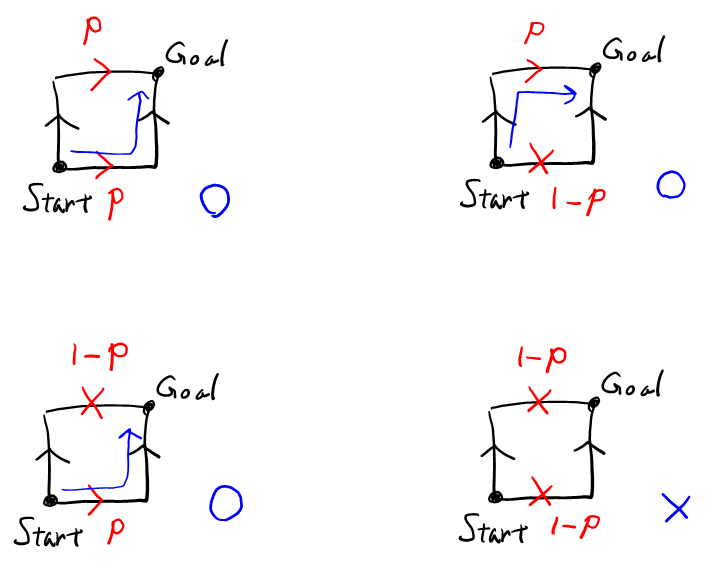
よって, ○となる3通りの確率を足し合わせて, \( Q_n = p^2 + p(1-p) + p(1-p) = p(2-p) \)。
\( Q_3 \)
誘導に乗る
横辺が4つになり, 全ての場合の数は\( 4^2 = 16 \)通りに増える。大変そうなので, \( Q_2 \)とのつながりを考えてみる。
\( Q_2 \)で, 正方形の左下から右上に移動できる確率を求めたので, もし, 最初に右へ移動できれば, あとは\( Q_2 \)の確率で最後まで到達できる(下図)。

また, 最初に右へ行けず, 上右と移動できる場合は, そこからさらに右へ一つ移動できれば最後まで到達できる(下図)。

よって, \( Q_3 = p \times Q_2 + p(1-p) \times p \)より求まる。
なお, 確率では排反な事象を抜けもれなく足し合わせなければならない。上の2通りですべての事象を重複なく尽くしているか自信がなければ, 以下のように場合分けをすれば確実であろう。

直接数える
適切に場合分けをして, 数え上げてみる。下の横辺で初めて×になる箇所で場合分けをすると, 以下の通りになる。

よって, \( Q_3 = (1-p) \times p^2 + p(1-p) \times p + p^2 \)
\( Q_n \)
誘導に乗る
\( Q_3 \)と同じようにして, \( Q_{n+1} \)と\( Q_n \)の漸化式を立てればよい。つまり, 以下の2通りで場合分けをする。
(i)最初に右に移動できる場合(確率\( p \))
最後まで到達できる確率は, \( p \times Q_n \)
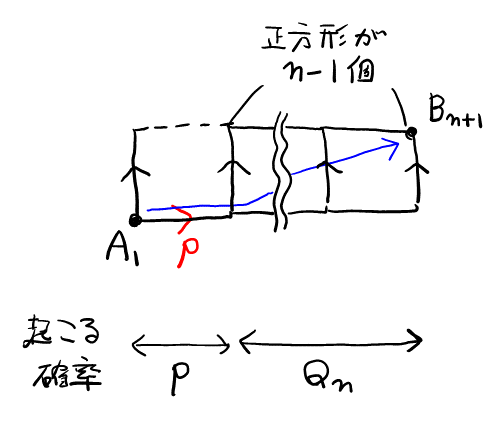
(ii)最初に右に移動できず, 上右と移動できる場合(確率\( p(1-p) \))
上右と移動した後, 右に\( n-1 \)回移動できればよいので, 最後まで到達できる確率は, \( p(1-p) \times p^{n-1} \)

よって, 漸化式は\( Q_{n+1} = pQ_n + p^n(1-p) \)となり, これを初期条件\( Q_2 = p(2-p) \)(または\( Q_1 = 1 \))のもとで解けばよい。
直接数える
\( Q_3 \)と同様に, 下の横辺で初めて×になる箇所で場合分けをすると, 以下のようになる(この図を書くのが少し面倒)。
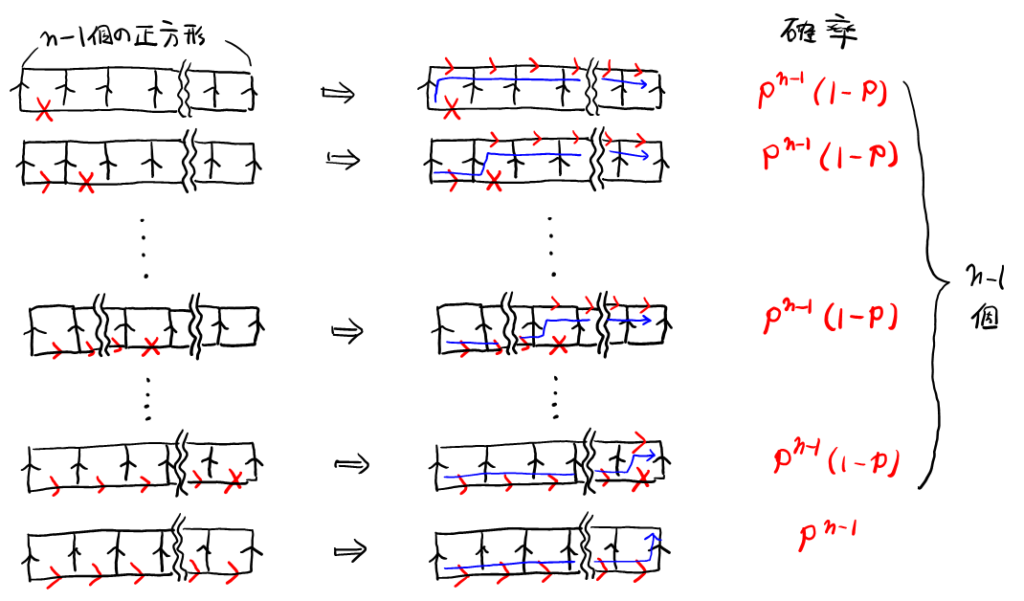
最後の場合以外は全て, 矢印と×の数が等しいので確率も等しくなり, それぞれの確率は\( p^{n-1}(1-p) \)。
最後の場合は, 矢印が\( n-1 \)個ある確率なので, \( p^{n-1} \)。
よって, これらの確率を全て足して, \( Q_n = (n-1) \times p^{n-1}(1-p) + p^{n-1} \)。
解答例
(1)
\( n=2 \)のとき, \( B_2 \)に到達するのは,
(i)\( A_1, A_2 \)が矢印の場合
(ii)\( A_1, A_2 \)が×で, かつ\( B_1, B_2 \)が矢印の場合
のいずれかであり, これらは排反ですべての場合を尽くす。
よって, \( Q_2 = p + p(1-p) = p(2-p) \)
\( n=3 \)のとき, \( B_2 \)に到達するのは,
(i)\( A_1, A_2 \)が矢印の場合
\( A_2 \)から\( B_3 \)まで到達すればよいので, \( p \times Q_2 \)
(ii)\( A_1, A_2 \)が×で, かつ\( B_1, B_2 \)が矢印の場合
\( B_2, B_3 \)が矢印であればよいので, \( p(1-p) \times p \)
よって, \( Q_3 = pQ_2 + p^2(1-p) = p^2(3-2p) \)
(2)
\( A_1 \)から\( B_{n+1} \)に到達するのは,
(i)\( A_1, A_2 \)が矢印の場合
\( A_2 \)から\( B_{n+1} \)まで到達すればよいので, \( p \times Q_n \)
(ii)\( A_1, A_2 \)が×で, かつ\( B_1, B_2 \)が矢印の場合
\( B_2, B_3 \sim B_n, B_{n+1} \)の\( n-1 \)個の横辺が全て矢印であればよいので, \( p(1-p) \times p^{n-1} \)
よって, \( Q_{n+1} = pQ_{n} + p^n(1-p) \)
整理して, \( \frac{Q_{n+1}}{p^{n+1}} – \frac{Q_n}{p^n} = \frac{1-p}{p} \)
等差数列だから, \( \frac{Q_n}{p} = \frac{Q_2}{p^2} + (n-2)\frac{1-p}{p} \)
したがって, \( Q_n = p^{n-1}(n+p-np) \)
振り返り
確率の基本的な問題であるが, 確率の基本を意識しないと, 漏れや重複により数え間違いが発生しやすい問題。確実に排反になるように場合分けをすることが大切。
また, 本問は誘導があるので気づきやすいが, 京大の確率は漸化式が頻出なので, 再帰的な構造に着目する意識を常に持っておこう。

コメント