問題
\( N \)を自然数とする\( N+1 \)個の箱があり, \( 1 \)から\( N+1 \)までの番号が付いている。どの箱にも玉が\( 1 \)個入っている。番号\( 1 \)から\( N \)までの箱に入っている玉は白玉で, 番号\( N+1 \)の箱に入っている玉は赤玉である。次の操作(*)を, おのおのの\( k=1, 2, \cdots, N+1 \)に対して, \( k \)が小さい方から順番に\( 1 \)回ずつ行う。
(*) \( k \)以外の番号の\( N \)個の箱から\( 1 \)個の箱を選び, その箱の中身と番号\( k \)の箱の中身を交換する。(ただし, \( N \)個の箱から\( 1 \)個の箱を選ぶ事象は, どれも同様に確からしいとする。)
操作がすべて終了した後, 赤玉が番号\( N+1 \)の箱に入っている確率を求めよ。
発想
状況を正確に理解するため, 小さい\( N \)で図を書いてみる。すると, 最後の箱に赤玉が入るためには, 最後の\( N+1 \)回目の操作でほぼ決まることがわかる。
下書き
\( N = 2, 3 \)くらいで図を書いて状況を掴む。まず\( N = 2 \)で樹形図を書く。
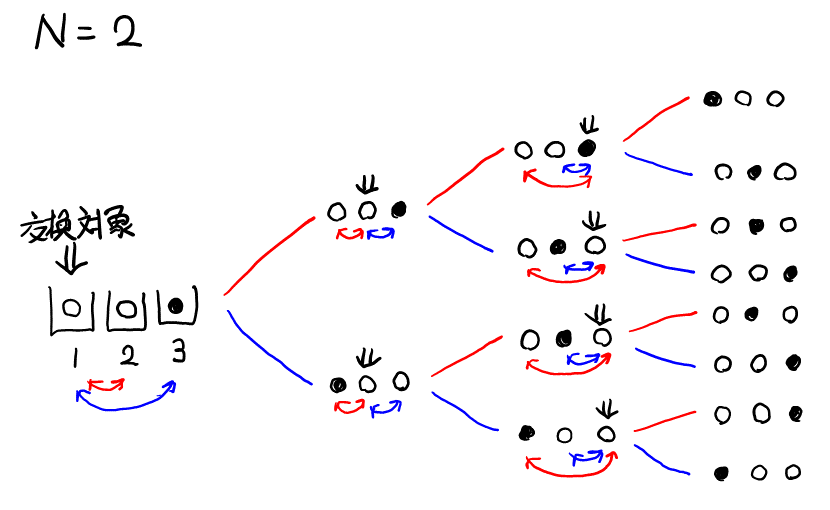
次に, \( N = 3 \)でも樹形図を書いてもよいが, 多くて大変そうなので, 最後の箱に赤玉が入る場合と入らない場合の具体例を書いてみる。
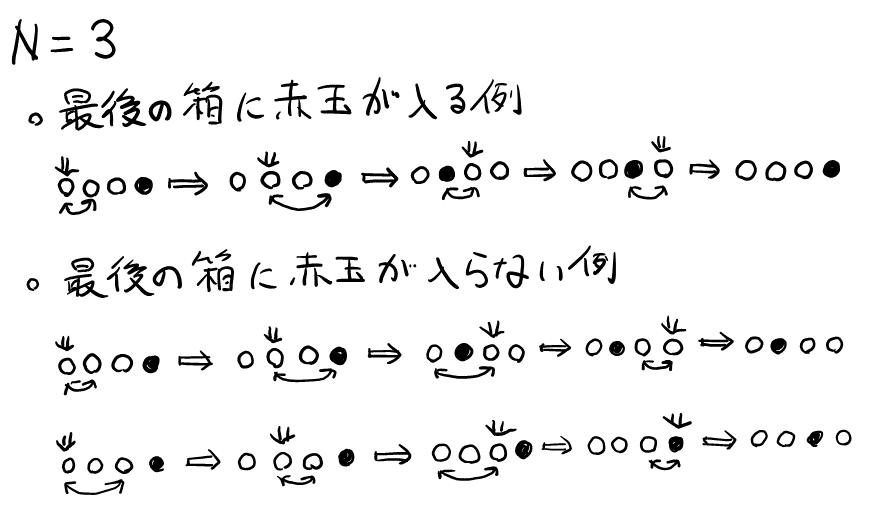
やっているうちに, よく考えれば当たり前だが, 最後の箱に赤玉が入っているためには, 最後の操作で赤玉を交換しないといけない, と気づく。よって, 最後の操作までのどこかで, 赤玉をどこかに移動しておく必要がある。
さらによく考えると, 一旦赤玉が移動してしまえば, 最後の操作以外で, 最後の箱に戻ってくることはないと気づく。
以上より,
・\( 1 \sim N \)回目のどこかで赤玉が移動する…①
・\( N+1 \)回目に赤玉が(最後の箱に)移動する…②
の2つがともに成り立てばよい。
まず\( N+1 \)回目に赤玉が(最後の箱に)移動する②の確率は簡単で, \( 1 \sim N \)番目の箱のどこかにある赤玉をピンポイントで選ぶ確率なので, \( \frac{1}{N} \)。
\( 1 \sim N \)回目のどこかで赤玉が移動する①の確率は, 少なくとも1回赤玉を選ぶ, と考えて, 余事象を使うと早い。つまり, \( N \)回の操作で1回も赤玉を選ばない確率は\( (\frac{N-1}{N})^N \)であるから, \( 1 \sim N \)回目のどこかで赤玉が移動する①の確率は\( 1- (\frac{N-1}{N})^N \)。
\( 1 \sim N \)回目のどこかで赤玉が移動する①かつ\( N+1 \)回目に赤玉が(最後の箱に)移動する②の確率を求めるので, これらを掛けたものが答えである。
解答例
\( 1 \sim N \)回目の操作で1度も番号\( N+1 \)の箱が選ばれないと, \( N+1 \)回目の操作で番号\( N+1 \)の箱に入っている赤玉が移動してしまうので, 赤玉が番号\( N+1 \)の箱に入っていることはない。
逆に, \( 1 \sim N \)回目の操作で少なくとも1回, 番号\( N+1 \)の箱が選ばれる(…①とする)と, \( N+1 \)回目の操作前には赤玉は番号\( 1 \sim N \)の箱のどこかにある。よって, \( N+1 \)回目の操作で赤玉が入った箱が選ばれる(…②とする)場合に限り, 赤玉が番号\( N+1 \)の箱に入っていることになる。
\( 1 \sim N \)回目の操作で少なくとも1回, 番号\( N+1 \)の箱が選ばれる①の確率は, 余事象を考えて\( 1- (\frac{N-1}{N})^N \), \( N+1 \)回目の操作で赤玉が入った箱が選ばれる②の確率は\( \frac{1}{N} \)だから, 求める確率は, \( \frac{1}{N}\{1- (\frac{N-1}{N})^N\} \)
補足(①の求め方の別解)
\( 1 \sim N \)回目のどこかで赤玉が移動する確率…①
の求め方については, 必ず余事象を思いついてもらわないと困るが, あえて余事象を使わないこともできる。こちらの考え方も重要なので取り上げておく。
\( 1 \sim N \)回目のどこかで赤玉が移動する確率①は, 以下のように考えても同じである。
\( k \)回目(\( k=1, 2, \cdots, N \))に初めて赤玉を選ぶ確率の和…①’
よって, \( k \)回目に初めて赤玉を選ぶ確率を求めて, \( k = 1 \sim N \)まで足し合わせると求めることができる。
\( k \)回目に初めて赤玉を選ぶ確率は, \( 1, 2, \cdots, k-1 \)回目までは白玉を選び続け, \( k \)回目に赤玉を選び, \( k+1 \)回目以降は何を選んでもよいので, \( (\color{blue}{\frac{N-1}{N}})^{k-1} \cdot \color{red}{\frac{1}{N}} \)となる。これらの和を求める際には, 等比数列の和の公式を使えばよい。\( \sum_{k=1}^N \{ (\frac{N-1}{N})^{k-1} \cdot \frac{1}{N} \} \)が\( 1- (\frac{N-1}{N})^N \)と一致することを確認すること。
振り返り
確率を求めること自体は簡単で, 立式が出来るかどうかの問題。立式するためには, 状況の把握が何よりも大切で, 必要があれば実験して, 正しく状況を理解する能力が問われている。
この問題では, 赤玉が一度でも移動したら\( N \)回目までは戻らないことと, \( N + 1 \)回目に赤玉を選ぶ必要があることに, 気づかなければいけない。そこがわかれば答えは出せるはずである。
それほど難しくない問題なので, 出来れば完答したい。

コメント