問題
次の文を読んで, に適した式を, それぞれの解答欄に記入せよ。
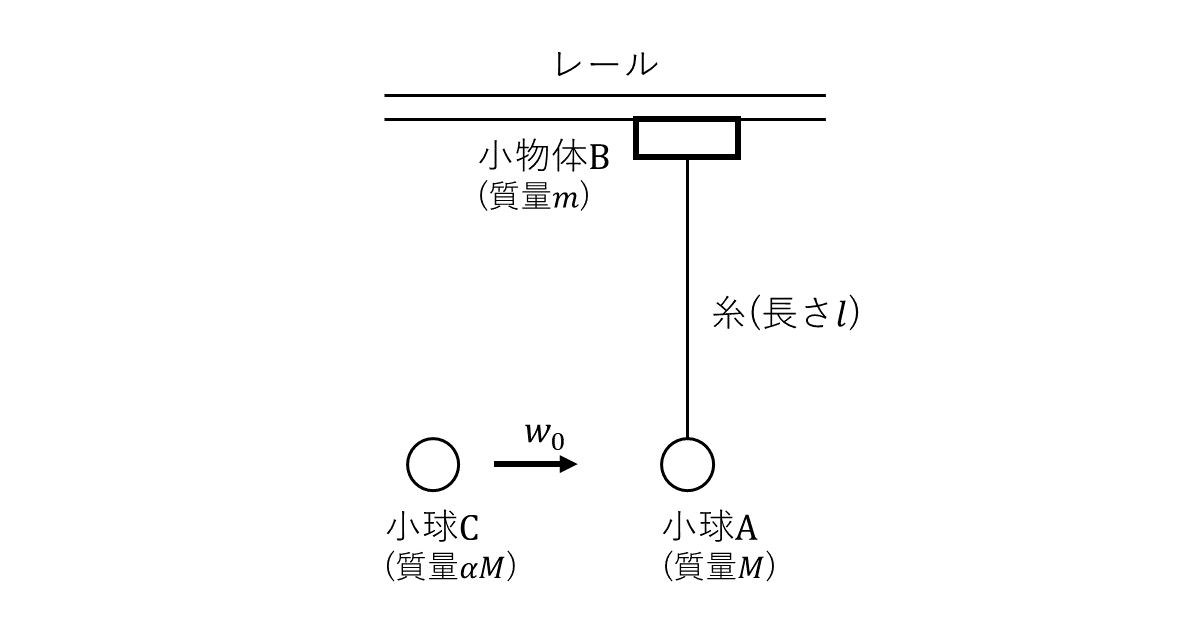
(1) 図1に示すように, 質量\( M \)の小球\( \rm{A} \)が, 質量を無視できる長さ\( l \)の伸びない糸でつり下げられており, 糸の他端にとりつけられた質量\( m \)の小物体\( \rm{B} \)は, 水平な直線レールに沿って滑らかに移動できるようになっている。重力加速度を\( g \)とし, 空気抵抗は無視できるとする。
はじめに, 図1の静止状態において, 小球\( \rm{A} \)の\( \alpha \)倍の質量\( \alpha M \)をもつ小球\( \rm{C} \)が, 水平右向きに速さ\( w_0 \)で小球\( \rm{A} \)に正面衝突し, 両球はたがいに水平方向にはねかえされた。小球\( \rm{A, C} \)の衝突後の運動は, レールを含む鉛直平面内に限られるものとする。衝突直後, 小物体\( \rm{B} \)はレールに沿ってすべりはじめたが, その初速度は\( 0 \)であった。小球\( \rm{A} \)と小球\( \rm{C} \)の衝突のはねかえりの係数(反発係数)が\( e \)であるとき, 衝突直後の小球\( \rm{A} \)の速さはイであり, 小球\( \rm{C} \)については, もし不等式ロが成り立てば右向きに運動し, その速さはハである。また, この衝突によって失われた全力学的エネルギーはニである。
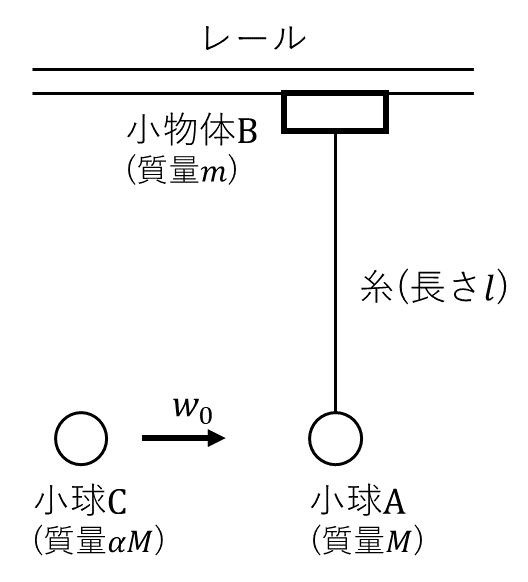
(2) (1)における衝突によって, 小球\( \rm{A} \)が得た水平右向きの初速度の大きさを\( u_0 \)と記し, 以下では, 衝突後の運動に関係する諸量を\( u_0 \)を用いて表すことにする。衝突の後, 小物体\( \rm{B} \)はレールに沿って移動しつつ, 糸は鉛直状態を中心にして左右に振れた。ただし, 振れの最大の角度は\( 90 \)度よりも小さかった。ある瞬間に, 小球\( \rm{A} \)の速度の水平成分(右向きが正)が\( u \)であり, 小物体\( \rm{B} \)のそれが\( v \)であった。\( u \)と\( v \)との間には等式ホが成り立たなければならない。一方, 同じ瞬間に, 小物体\( \rm{B} \)から距離\( x \)だけ離れた糸上の点がもつ速度の水平成分は, 糸が直線状であることに注意すれば, \( u, v, l, x \)を用いてヘのように表される。これら二つの関係から, \( x= \)トの点の速度は常に一定の水平成分チをもつことがわかる。
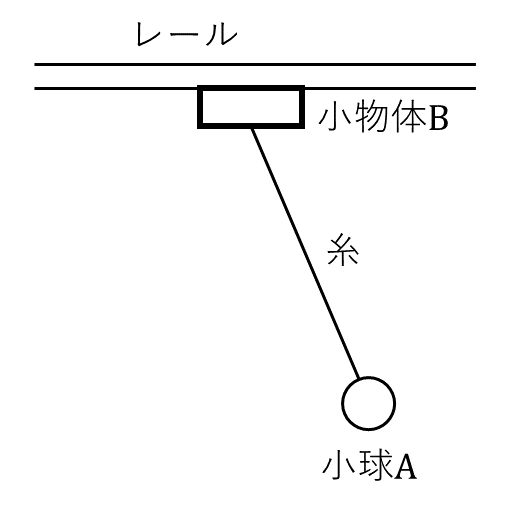
(3) 糸が図2に示されるように右に振れ切った瞬間, 小球\( \rm{A} \)は水平方向にのみ速さリをもち, 最低点からヌだけ高い位置にある。その後はじめて糸が鉛直になった瞬間における小球\( \rm{A} \)の運動は, もし不等式ルが成り立てば右向きであり, その速さはヲである。また, 同じ瞬間における小物体\( \rm{B} \)の速さはワである。
解説
(1)
(1)は小手調べ。典型問題なので解説は省略する。
(2)
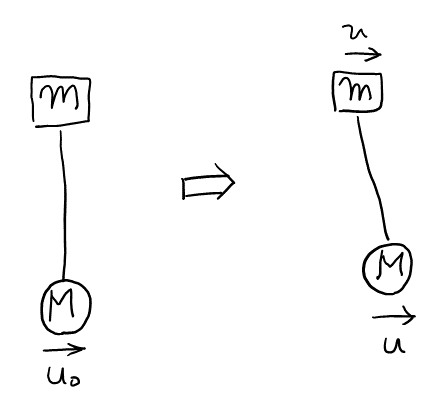
ホ
運動量保存則で一発。\( Mu_0 = mv + Mu \)…①となる。
ヘ
差が付くポイント。見ないタイプの問題なので, 図をよく見て考える。以下のようにシンプルに書き換えれば, ただの比の問題だと分かる。
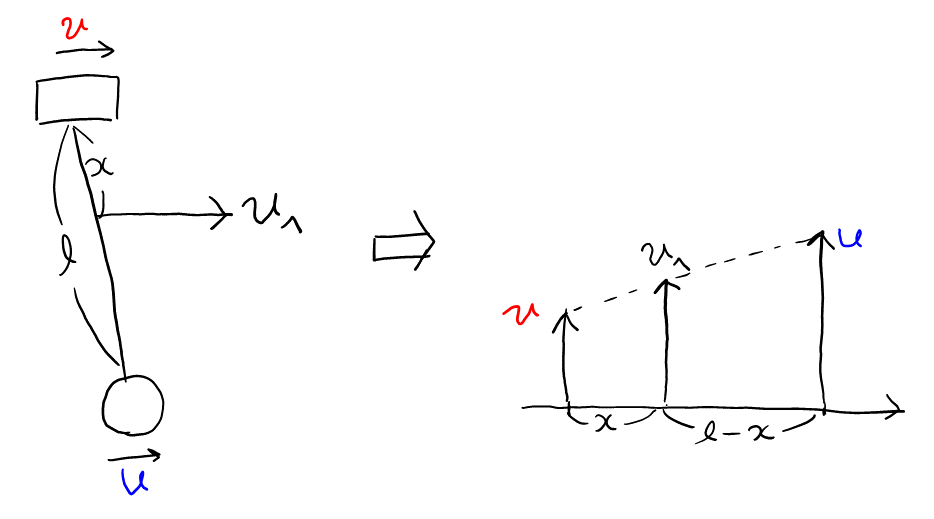
\( v_ヘ \)は, \( \color{red}{v} \)と\( \color{blue}{u} \)を\( x : l-x \)に内分したような速度になるので, 逆比になることに注意して, \( v_ヘ = \frac{x}{x + (l-x)}\color{blue}{u} + \frac{l-x}{x + (l-x)}\color{red}{v} \)となる。\( x = 0 \)や\( x = l \)を入れて検算すること。
逆に, \( x = 0 \)のとき\( v_ヘ = v \), \( x = l \)のとき\( v_ヘ = u \)になることを使って, \( v_ヘ \)を求めてもよい。ほぼ明らかに一次関数的な変化なので, 2点の情報がわかれば求まる。\( (0, v), (l, u) \)を通る直線を求める要領で, \( v_ヘ = \frac{u-v}{l}x + v \)となる。
トチ
「常に一定の水平成分」とあるので, 慣れた人なら重心速度一定の法則を思い浮かべるはず。これを(何となくでも)知っていれば, 決め打ちで重心の\( x \)を入れて, \( v_ヘ \)が一定になるかを確かめればよい。
重心の\( x \)は, 再びシンプルな図を書くと,
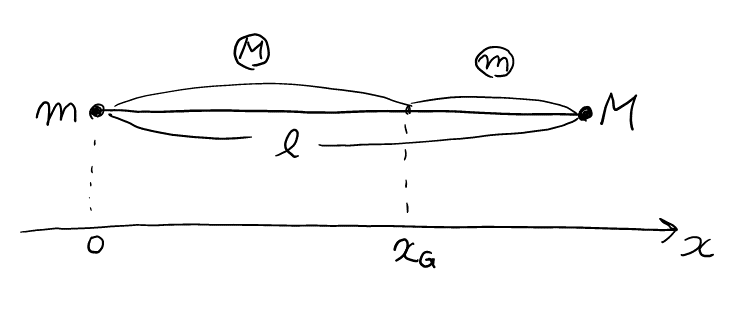
長さ\( l \)を\( M:m \)(逆比)に内分する点だとわかるから, \( x_G = l \times \frac{M}{M+m} \)となる。
これを\( v_ヘ \)に入れて少し計算すると, \( v_ヘ = \frac{mv + Mu}{M+m} \)となるが, \( Mu_0 = mv + Mu \)①よりこれは一定となる。よって\( x \)は重心であるという”あたり”は正しかったとわかる。
重心速度一定を使わない場合は, ホとヘから\( v \)を消去して\( u \)だけの式にし, \( u \)の係数\( =0 \)と考えるよい。
(3)
リヌ
よくある設定であり, 振れ切った瞬間は\( \rm{A} \)と\( \rm{B} \)の速度が同じだとすぐに気づかないといけない(\( \rm{B} \)から見ると, \( \rm{A} \)は一瞬止まって見えるから)。
リは運動量保存則で瞬殺, ヌもいつも通りエネルギー保存則で一発。
ルヲワ
ここも特に難しくはなく, 運動量保存とエネルギー保存を連立すればよいだけ。分かりにくい場合は図を書いて考えること。
問題文より, \( v_ワ \)の方は場合分けなく一意に求まりそうなので, まず\( v_ヲ \)を消去して\( v_ワ \)から出すとよいだろう。
振り返り
(2)がポイントで, テーマは重心速度一定である。ただ, 本問を解く場合は, 詳しく知っていなくてもよい。いずれにせよ, (2)は解けたら安心レベルの難易度なので, 初めのうちは解けなくても心配する必要はない。
こういう大問では, (1)を落とさないことが大切である。10分ほどかけてよいので, 確実に正解すること。
また, 京大物理によくあることだが, (2)より(3)の方が簡単で, 特にリなどは一瞬で求まる。このような問題後半の簡単な問題を目敏く見つける感覚も養ってほしい。
コメント