問題
次の文を読んで, に適した式または数をそれぞれの解答欄に記入せよ。
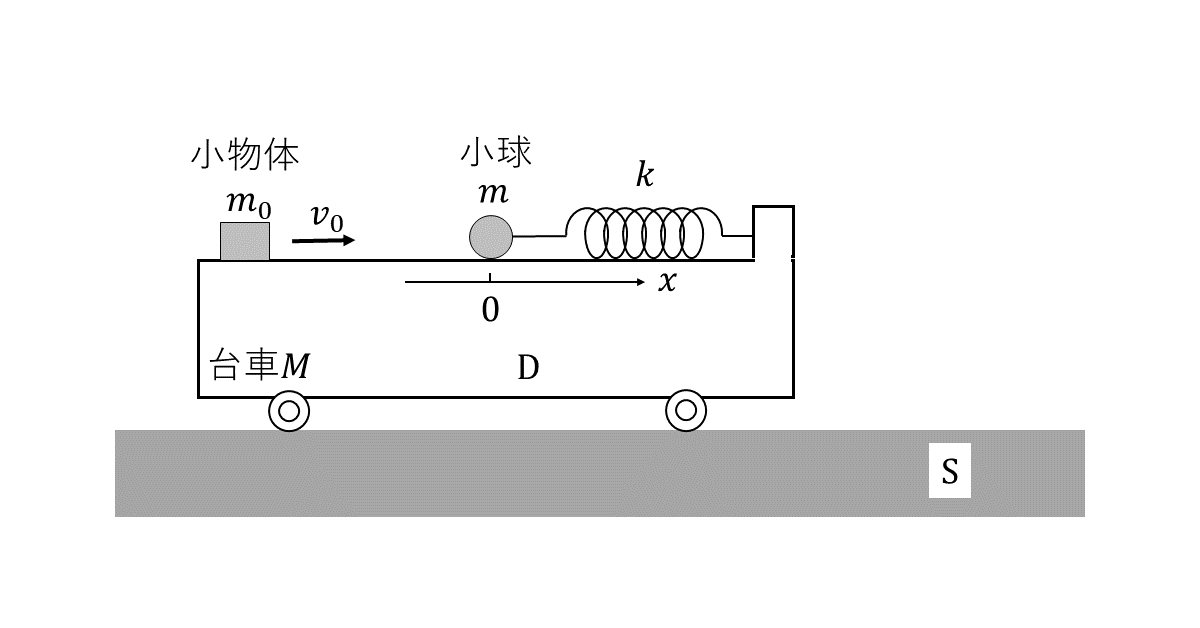
図1のように, 水平な床の上を摩擦なしに動くことのできる質量\( M[\rm{kg}] \)の台車がある。台車上で, 質量\( m[\rm{kg}] \)の小球がばね定数\( k[\rm{N/m}] \)のばねで台車の端につながれ, 一方の端には質量\( m_0[\rm{kg}] \)の小物体が置かれている。はじめ, ばねは自然長であり, 台車, 小球, および小物体は静止している。小物体を速度\( v_0[\rm{m/s}] \)で小球に向けて滑らせた後の, 台車, 小球, および小物体の運動について考える。以下, 台車に固定した座標系を\( \rm{D} \), 床に固定した静止座標系を\( \rm{S} \)と呼ぶ。座標系\( \rm{D} \)での小球の位置は, ばねが\( x[\rm{m}] \)縮んだときを正, 伸びたときを負として座標\( x \)で表す。座標系\( \rm{S} \)では右方向を正とする。運動はすべて同一鉛直面内で起こり, ばねは質量が無視でき十分長く, 台車と小球の間の摩擦は常に無視できるとする。重力加速度の大きさを\( g[\rm{m/s^2}] \)とする。
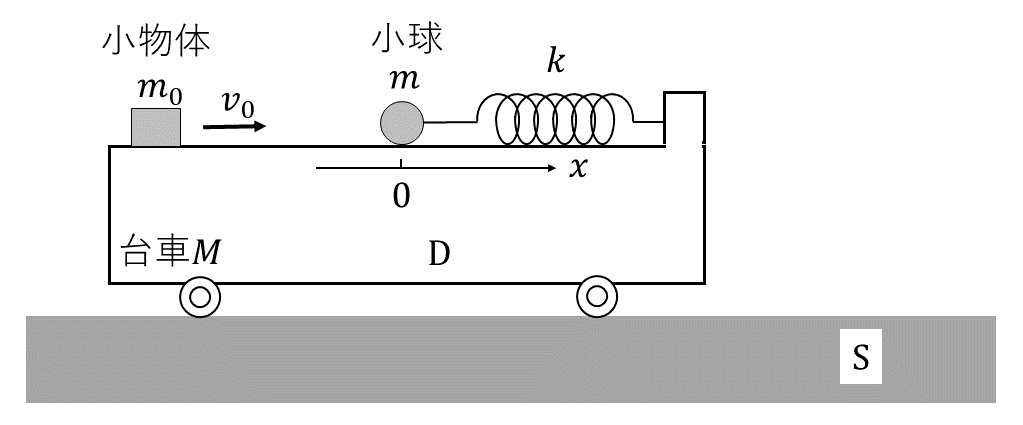
(1) 小物体と台車の間の摩擦が無視でき, 小物体は一回だけ小球と完全弾性衝突をし, 以後小球と衝突することはなかったとする。衝突直後の小物体の速度はイ\( [\rm{m/s}] \), 小球の速度\( v[\rm{m/s}] \)は\( v= \)ロである。ここで, 衝突後の台車と小球の運動を考えよう。小球の座標が\( x \)であるとき, 座標系\( \rm{S} \)で台車の運動を観測すると, 台車の加速度\( b[\rm{m/s^2}] \)は, \( b= \)ハである。この時の座標系\( \rm{D} \)での小球の加速度を\( a[\rm{m/s^2}] \)とすると, 小球の運動方程式は\( b \)を用いて\( ma= \)ニと書ける。この式から, 座標系\( \rm{D} \)での小球の運動は単振動であり, その周期はホ\( [\rm{s}] \), 振動の中心は\( x= \)ヘであることがわかる。
この単振動の振幅を求めるために, ばねが最も縮んだ時を考える。この時の座標系\( \rm{S} \)での台車と小球の速度は, 両者の相対速度が\( 0 \)であることと運動量保存則を使って, \( v \)を用いてト\( [\rm{m/s}] \)と表される。この結果とエネルギー保存則を使うと, 振幅は\( v \)を用いて, チ\( [\rm{m}] \)と表されることがわかる。
(2) 次に, 小物体と台車の間に摩擦があり, 小物体は小球に衝突することなく台車上で静止したとする。小物体が静止するまでの運動を考える。ただし, 動摩擦係数を\( \mu \)とする。小球の座標が\( x \)であるとき, 座標系\( \rm{S} \)での台車の加速度\( b'[\rm{m/s^2}] \)は\( b’= \)リである。この時の座標系\( \rm{D} \)での小球の加速度を\( a'[\rm{m/s^2}] \)とすると, 小球の運動方程式は\( b’ \)を用いて\( ma’= \)ヌと書ける。これより, 座標系\( \rm{D} \)での小球の運動は単振動であり, その中心は\( x= \)ルであることがわかる。
解説
問題文をざっと読み, 摩擦力は基本働かないが, (2)になると小物体と台車の間にだけ摩擦力が働くことに注意しておく。
(1)
イロ
いつも通り運動量保存則の式と反発係数の式を連立するだけ。必ず図を書いて, 正負を間違えないように注意。
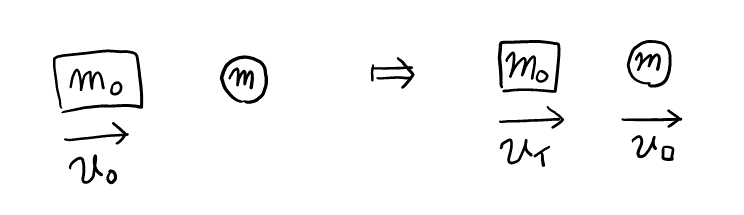
問題で問われてはいないが, 「以後小球と衝突することはなかった」とあるので, 小物体は左に進んだ, つまり\( v_イ < 0 \)より\( m_0 < m \)であることがわかる。
ハ
地面から見ているので, 慣性力は関係ない。台車に注目して図を書く。
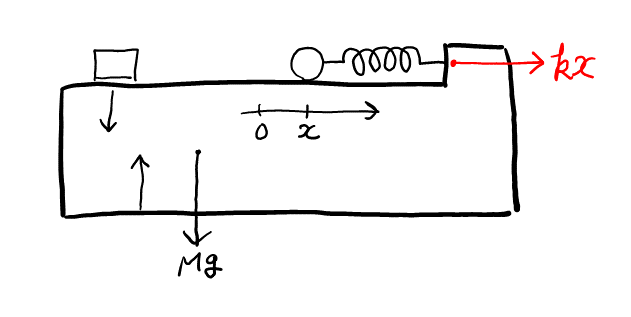
台車には, 弾性力のみが水平方向に働き, 運動方程式が書ける。
ニ
今度は台車に乗っているので, 慣性力が働く。小球に注目して図を書く。
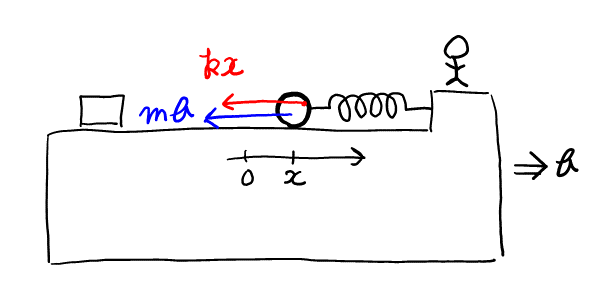
小球には, 弾性力と慣性力が水平方向に働き, 運動方程式が書ける。
ホへ
\( ma = -K(x-x_0)(k>0) \)の形で表せたら単振動であり, このとき, 振動中心は\( x_0 \), 角振動数\( \omega = \sqrt{\frac{K}{m}} \)となる(\( \omega \)がわかれば\( T \)もわかる)。よって, \( ma = -K(x-x_0) \)を目指して変形していく。
ハをニに代入して式変形すると, \( ma = -\frac{k(M+m)}{M}x \)となるので, \( K=\frac{k(M+m)}{M} \), \( x_0=0 \)の場合だとわかる。
トチ
簡単なので省略。
(2)
小物体は小球には到達しないが, 摩擦力が働くので, 台車が動き, その結果ばねが伸び縮みすることに注意する。摩擦力の向きは, もちろん運動を妨げる向きと考えてもよいが, 小物体が台車を「引きずっている」イメージを持つとわかりやすいかもしれない。
リ
地面から見ているので, 慣性力は関係ない。台車に注目して図を書く。
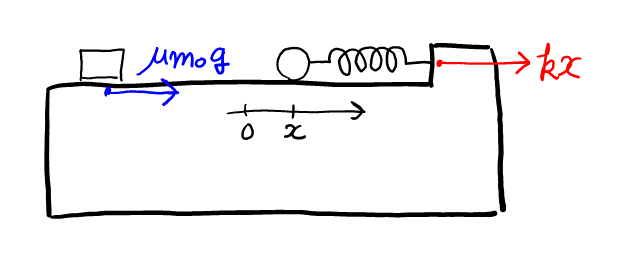
台車には, 弾性力に加えて, 動摩擦力が水平方向に働き, 運動方程式が書ける。
ヌ
今度は台車に乗っているので, 慣性力が働く。小球に注目して図を書く。
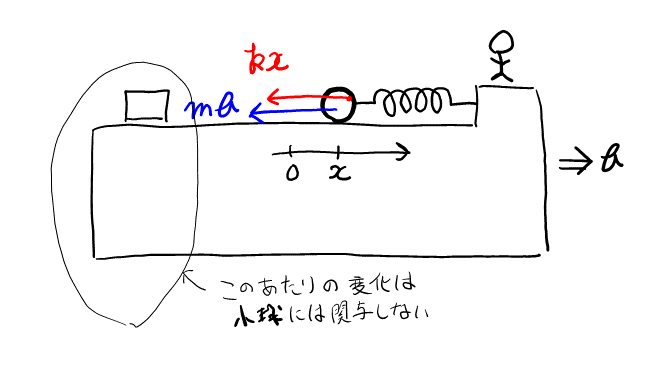
小球には, 弾性力と慣性力が水平方向に働き, 運動方程式が書ける。結果的にニとほとんど同じになってしまうので, 見逃している力が無いか, 慎重に見直してから答えを書く。
ル
ホへと同様に, \( ma = \underline{-K(x-x_0)} \)を目指して変形していく。やってみると分かるが, 意外と変形が大変なので, 全て展開した形で比較すると良い。つまり, 目指す形は\( ma = \underline{-\color{red}{K}x+\color{blue}{Kx_0}} \)のように, \( x \)の項と定数項に分けて考える。
リをヌに代入して頑張って計算すると, \( ma’ = -\color{red}{\frac{k(M+m)}{M}}x \color{blue}{- \frac{\mu mm_0g}{M}} \)となるので, \( \color{red}{K} = \frac{k(M+m)}{M} \), \( \color{blue}{Kx_0} = – \frac{\mu mm_0g}{M} \)の場合だと分かり, ここから\( K \)を消去して\( x_0 \)が求まる。
振り返り
決して難しくはないが, こういう問題で8~9割確保することがいかに大切かということがわかるような問題。特に最後の問題などは計算も多少時間がかかり, 差が付きやすい。単振動は京大頻出分野であるので, 重点的に見直しておきたい。
コメント