問題
次の文を読んで, には適した式を, には適した数値を, それぞれの解答欄に記入せよ。
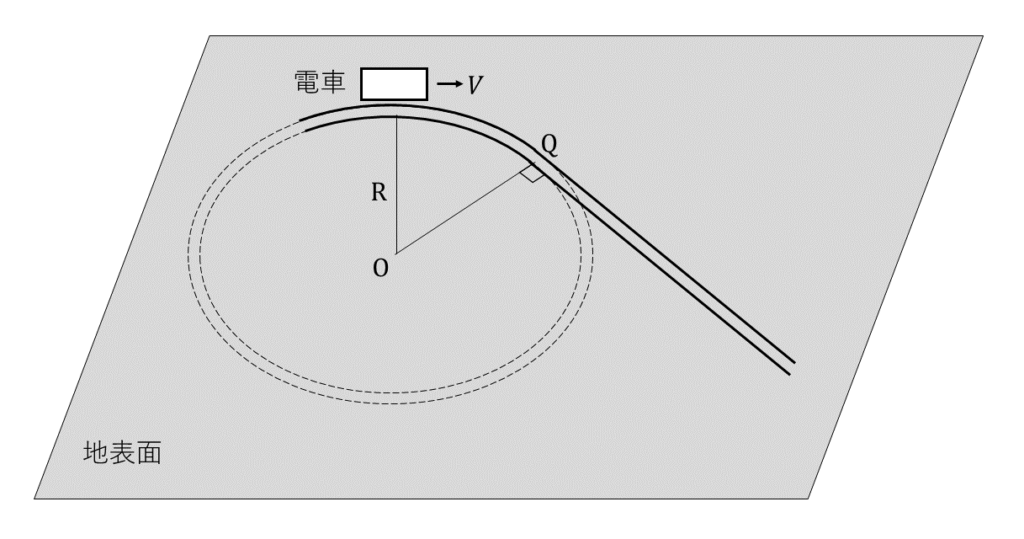
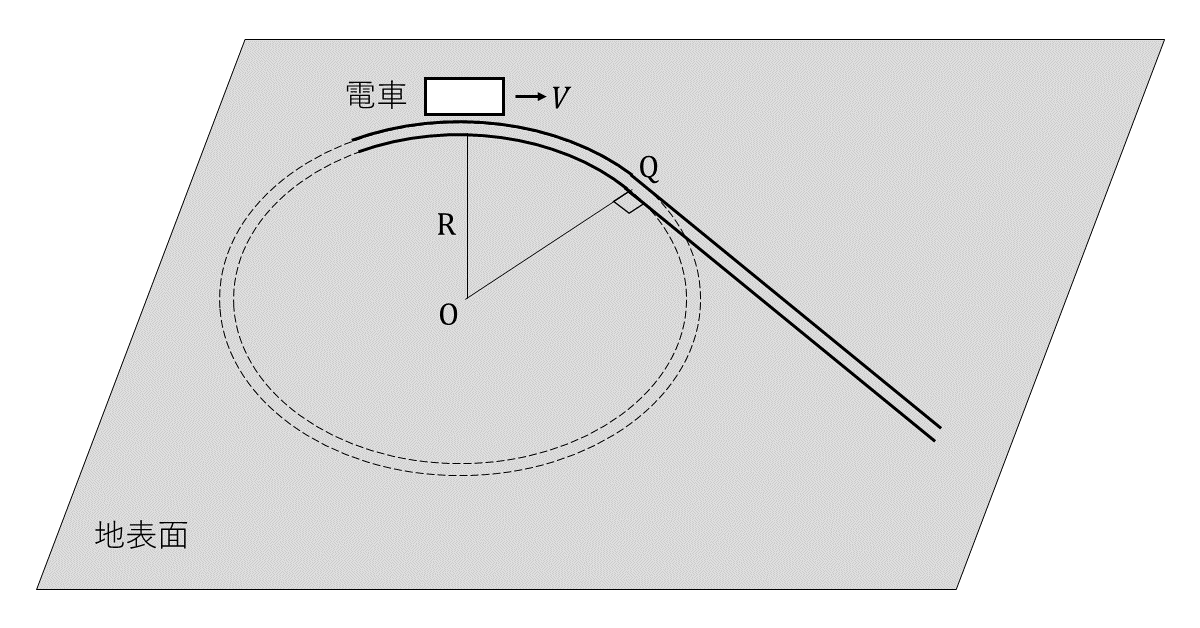
図1のように, 水平な地表面上に敷かれたレール上を電車が一定の速さ\( V \)で動いているとする。このレールは, 点\( \rm{Q} \)の手前で点\( \rm{O} \)を中心とした半径\( R \)の円弧状であり, 点\( \rm{Q} \)の先では点\( \rm{Q} \)で円弧に接する直線状となっている。レールの幅, 電車の幅, 長さ, 高さはいずれも, \( R \)に比べて非常に小さいとする。以下の(1)~(3)では電車が円弧状のレール上を動いているときについて, (4)では電車が直線状のレール上を動いているときについて, 車内での小物体の運動を考える。ここで, 重力加速度の大きさを\( g \)とし, 小物体の大きさと小物体に対する空気の抵抗はいずれも無視する。
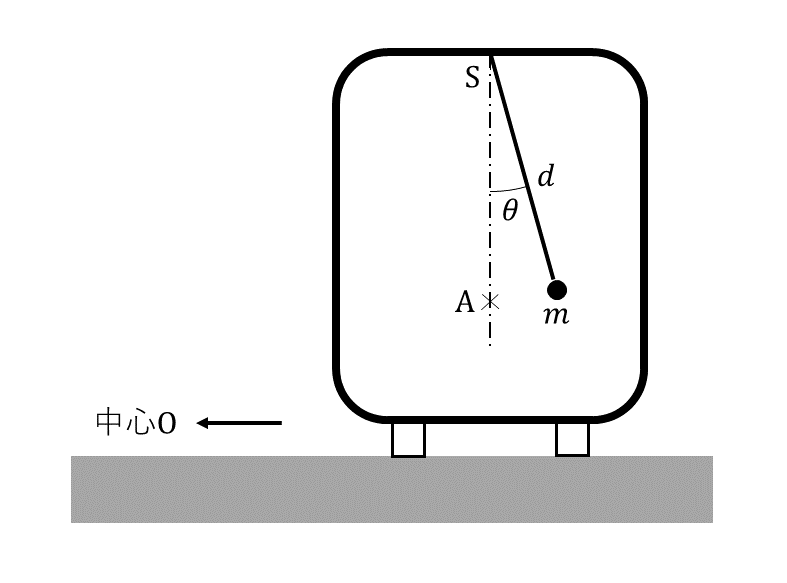
(1) 電車が点\( \rm{Q} \)の手前の円弧上のレール上を走っているとき, 図2のように, 電車の天井の点\( \rm{S} \)から, 質量の無視できる長さ\( d \)の意図でつるされた質量\( m \)の小物体は, 車内の観測者から見て静止していた。なお, 図2はこの電車を進行方向から見たところであり, 図の左方向が中心\( \rm{O} \)の方向である。また, 点\( \rm{A} \)は電車が動いていないときの小物体の静止位置である。このとき, 車内の観測者には, 車内の小物体に大きさアの遠心力が働いているように見えるので, 糸が円直線\( \rm{SA} \)となす角\( \theta \)は\( \tan \theta = \)イを満たす。また, 糸の張力\( T \)と重力\( mg \)との比は\( \theta \)のみを用いて, \( T / (mg) = \)ウと表される。
(2) 小物体が車内の観測者から見て動いているときでも, その速さが\( V \)に比べてじゅうぶんに小さければ, 短い間に電車の加速度運動が小物体へ及ぼす影響は, 大きさアの遠心力の見に表れると近似的に考えることができる。以下, この近似を使って考えることにする。この場合, 車内の観測者から見て小物体には常に重力大きさアの遠心力の合力が働くので, あたかも重力加速度の方向と大きさが変化したように見える。この見かけの重力加速度の大きさを\( g’ \)とすると, \( g’ \)と\( g \)の比は\( \theta \)のみを用いて表すことができて, \( g’ / g = \)エとなる。
(3) 小物体を点\( \rm{A} \)から, 車内の観測者から見て速さ\( u \)で電車の進行方向に押し出した。この後, 小物体は車内の観測者から見て円運動をした。この円運動の半径は\( d \)と\( \theta \)を用いて表すとオである。また, 速さ\( u \)は\( d, g’, \theta \)を用いて表すと\( u = \)カであり, 円運動の周期は\( d, g’, \theta \)を用いて表すとキとなる。
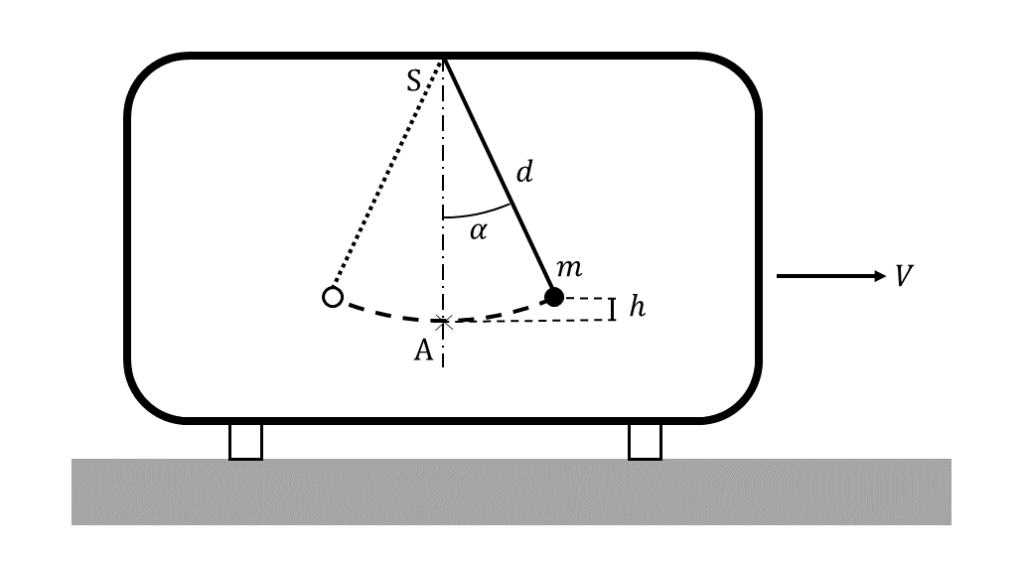
(4) この小物体が(3)のように円運動をしていて, ちょうど点\( \rm{A} \)を通過したときに, 電車は図1のレール上の点\( \rm{Q} \)を通過し, 直線状のレールに速さ\( V \)のまま移った。この直線状のレール上を走っているとき, 車内の観測者が見ると, 図3のように, 小物体は点\( \rm{A} \)を中心とする振動をした。この振動において, 点\( \rm{A} \)からはかった小物体の最高位置の高さ\( h \)は\( u \)と\( g \)を用いて, \( h = \)クと表される。したがって, この振動において糸が鉛直線となす最大の角度を\( \alpha \)として, \( g’ / g = \)エと\( u = \)カの結果を使って, \( \cos \alpha \)を\( \tan \theta \)のみを用いて表すと, \( \cos \alpha = \)ケとなる。ここで, \( \alpha \)も\( \theta \)も小さいとして\( \cos \alpha \fallingdotseq 1 – \alpha^2 / 2 \)および\( \tan \theta \fallingdotseq \theta \)と近似すると, \( \alpha \fallingdotseq \)コ\( \times \theta \)となる。
解説
慣性系と非慣性系を明確に区別することが大切。
非慣性系→加速運動中の物体から見た世界。慣性力\( ma \)が働く。
慣性系→加速度0の物体から見た世界。\( ma = F \)が成り立つ。
本問では, (1)~(3)は等速円運動(つまり, 加速度あり)をしているので, 電車内は非慣性系。
(4)では, 等速直線運動(つまり, 加速度なし)をしているので, 電車内は慣性系。
(1)
等速円運動における慣性力は, 遠心力である。アは公式そのまま。
次に遠心力を考慮して図を書くと, よく見る図になる。いつも通り水平方向と鉛直方向の2式を立てて, \( T \)と\( \theta \)を未知数として解けばよい。
(2)
「見かけの重力加速度」はよく出てくるので, 確実に理解しておく。遠心力がない世界では\( T_0 = m \color{red}{g} \)でつりあっていたのが, 遠心力がある世界では\( T = m \color{red}{\frac{g}{\cos \theta}} \)でつりあうことになるので, 式を見比べると, 遠心力がある世界での重力加速度は\( \frac{g}{\cos \theta} \)とみなせる。これが見かけの重力加速度である。
(3)
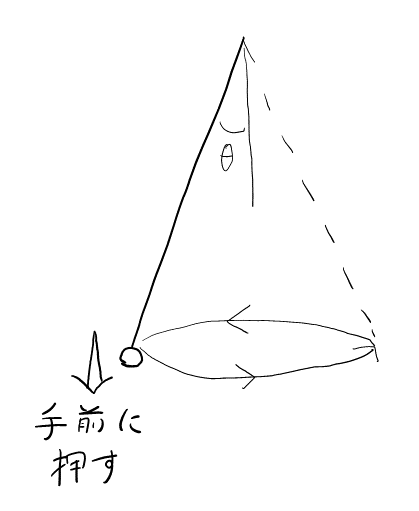
まず, 運動のイメージが掴めただろうか。分かりにくい人は, 慣性力が働かない「普通」の世界の運動から考えてみると良い。図4のように, 振り子を傾けた状態から, 垂直に押し出すときの運動はイメージできるはずである。ここから類推すると, 見かけの重力が働く「斜め」の世界では, 図5のようになる。このイメージさえ掴めればこの問題は十分である。
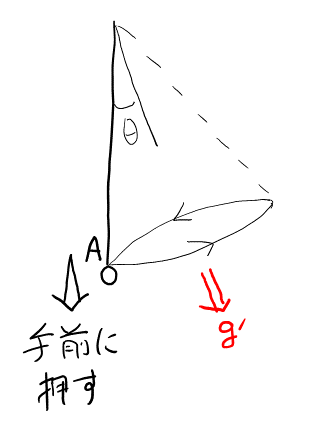
実際, オは図から直ちに分かり, カも通常の円錐振り子と同様に解けばよい(円運動の中心方向と垂直な方向の2式を連立して, 張力\( T’ \)を消去)。キは公式そのまま。
(4)
最初に述べたように, ここからは慣性系となる。車内から見た世界は, もはや「普通」の世界に戻っていることに注意する。
さて, ここでも運動のイメージが少しつきにくい。(3)では円運動をしていたのが, (4)では1次元的な運動になっている。これは, 図5の点\( \rm{A} \)でちょうど, (3)から(4)に切り替わったと考えると, 上手く説明がつく。
以上の観察から, (4)に切り替わった瞬間は最下点であり, そのときの速さは(3)から引き継いだ\( u \)である。
ここまで分かれば, エネルギー保存則を使った基本中の基本問題だと分かる。コはあまり見ない問題だが, ここまでこれば難なく解答できるだろう。
振り返り
(1)(2)までは確実にできなければならない。(3)が本問のポイントで, 見かけの重力のもとでの運動をイメージできるかどうか。(4)は(3)を乗り切った人には難しくないはず。
全体的に, 京大基準ではやや簡単レベルなので, 途中間違えてしまった人は, この問題が完答できるようになることを目指そう。
コメント