問題
次の文を読んで, には適した式または数値を, { }からは適切なものを選びその番号を, それぞれの解答欄に記入せよ。なお, はすでに または{ }で与えられたものと同じものを表す。また, 問1, 問2では指示にしたがって, 解答をそれぞれの解答欄に記入せよ。
以下の設問では, 向心力を受けて円運動する物体について摩擦力による速さの変化を考える。その際, さまざまな物理量の微小な変化を調べる。
(1)
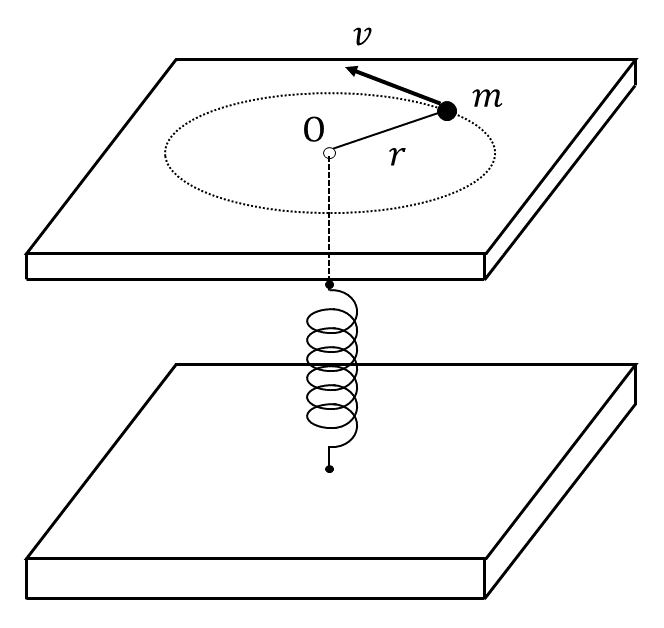
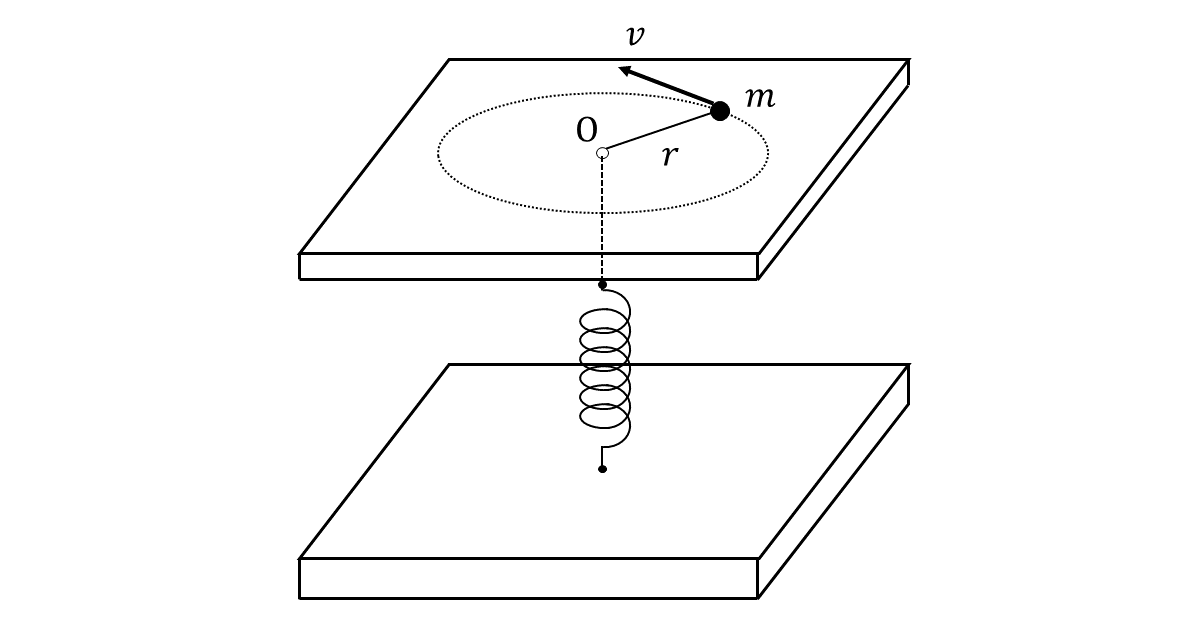
図1のように, 滑らかな台の上に置かれた質量\( m \)の物体が, ひもにつながれている。ひもは台の中心\( \rm{O} \)に開けられたなめらかな小さな穴を貫通し, ばねにつながれている。さらにばねの下端は下側の台に固定されている。この物体は半径\( r \), 速さ\( v \)の等速円運動をしている。ばね定数は\( b \)であり, ばねとひもの質量は無視してよいものとする。また, 物体が点\( \rm{O} \)にあるとき, ばねの長さが自然の長さであるようになっている。
この等速円運動に対する運動方程式は\( \frac{mv^2}{r} = \)アとなる。物体の運動エネルギーは\( K = \frac{1}{2}mv^2 \), ばねの弾性力の位置エネルギーは\( V = \frac{1}{2}br^2 \)で与えられる。このとき運動方程式から運動エネルギー\( K \)と位置エネルギー\( V \)の間に{イ:①\( K = V \) ②\( K = -V \) ③\( 2K = V \) ④\( 2K = -V \) ⑤\( K = 2V \) ⑥\( K = -2V \)}という関係が成り立つことが分かる。
(2)
次に, この物体に速度と逆方向に摩擦力が作用した場合を考える。摩擦力の大きさ\( D \)は一定とする。ばねの力に比べて非常に小さい摩擦力が作用したため, 図2のように軌道がわずかに円運動から変化したとしよう。そのため, 物体の速度は(1)で考えた速度と厳密には異なっている。ただし, 摩擦力が非常に小さい場合には, 速度の差はわずかであるので無視してよいものとする。物体の速さを\( v \)とすると, 図2のように微小な時間\( \varDelta t \)の間の移動距離は\( \varDelta s = v \varDelta t \)で与えられる。この移動の結果, 物体と点\( \rm{O} \)との距離は\( r \)から\( r – \varDelta r \)に変化する。実際には\( r \)に比べてその変化\( \varDelta r \)は非常に小さいが, この図では微小な変化\( \varDelta r \)を強調している。また, 物体の運動方向とばねによる向心力の間の角度\( \alpha \)は\( 90 {}^\circ \)よりわずかに小さい。
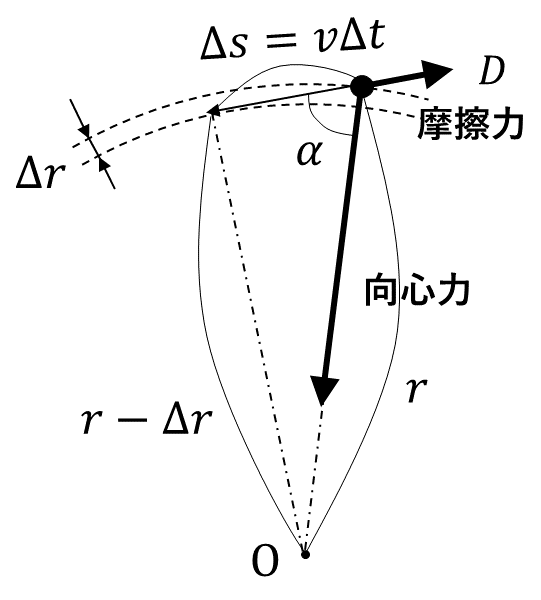
この微小な時間\( \varDelta t \)の間に生じる運動エネルギーの微小な変化\( \varDelta K \)は, ばねの力による仕事と摩擦力による仕事で決まるので, \( \varDelta K = ( \)ウ\( ) \times \varDelta s \)と与えられる。\( \varDelta s \)と\( \varDelta r \)が微小であることより, \( \varDelta s \cos \alpha = \varDelta r \)が成り立つとする。運動エネルギーの微小な変化\( \varDelta K \)のうち, ばねによる仕事は, 半径の微小な変化\( \varDelta r \)に比例する形でエと表される。このばねによる仕事と位置エネルギーの微小な変化の関係を調べよう。軌道の半径が\( r \)から\( r – \varDelta r \)に微小に変化する間に, 位置エネルギーは
$$\begin{eqnarray}
\varDelta V &=& \varDelta \left(\frac{1}{2}br^2\right) \\
&=& \frac{1}{2}b(r – \varDelta r)^2 – \frac{1}{2}br^2 \\
&=& -br\varDelta r + \frac{1}{2}b(\varDelta r)^2 \\
&\fallingdotseq& -br\varDelta r
\end{eqnarray}$$
だけ微小に変化する。上式の最後の行では, 微小な変化\( \varDelta r \)の2次の項\( \frac{1}{2}b(\varDelta r)^2 \)を無視している。このように, 本問題では微小な変化の2次の項は無視してよい。したがって運動エネルギーの微小な変化のうち, ばねによる仕事の部分は{オ:①\( +1 \) ②\( -1 \) ③\( +\frac{1}{2} \) ④\( -\frac{1}{2} \)}\( \times \varDelta V \)となる。また摩擦力による仕事は, 微小な時間\( \varDelta t \)に比例する形でカと表すことができる。したがって, \( \varDelta t \)の間に生じる力学的エネルギー\( E = K + V \)の微小な変化\( \varDelta E = \varDelta K + \varDelta V \)は
\( \varDelta E = \)カ (i)
と与えられる。
摩擦力が非常に小さいので, 物体は近似的に円運動を保ちながら, 少しずつ速さと半径が変化していくとする。このとき関係式イは成り立っていると考えてよい。したがって, 微小な変化\( \varDelta K, \varDelta V \)についても, 同じ関係を保ちながら, 力学的エネルギーが\( \varDelta E = \)カと微小に変化していくので, 運動エネルギーの微小な変化は
\( \varDelta K = \)キ\( \times ( \)カ\( ) \) (ii)
となる。(注:キには適切な数値を入れなさい。)
(3)
上の(2)では微小な時間\( \varDelta t \)の間の運動エネルギーの微小な変化を求めた。この間に, 物体の速さは\( v \)から\( v + \varDelta v \)に変化するので, 運動エネルギーの微小な変化は\( \varDelta K = \varDelta \left( \frac{1}{2}mv^2 \right) \fallingdotseq mv\varDelta v \)とも表せる。この式と式(ii)より, 物体の速さ\( v \)の変化率は
\( \displaystyle \frac{\varDelta v}{\varDelta t} = \)ク (iii)
と与えられる。式(iii)は直線上の等加速度運動と同じ形をしている。時刻\( t = 0 \)での物体の速さを\( v_0 \)とすると, 時刻\( t \)での物体の速さは\( v(t) = \)ケとなる。
(4)
これまでは, 物体がばねの力と小さい摩擦力を受けて近似的に円運動する場合を考えてきた。今度は, 図3のように, 質量\( M \)の地球の周りを運動する質量\( m \)の人工衛星について, これまでと同じような計算を行う。地球の中心から人工衛星までの距離を\( r \)とする。人工衛星には地球からの万有引力と, 大気から受ける小さい空気抵抗力が作用している。ただし, 人工衛星の質量\( m \)は地球の質量\( M \)に比べて非常に小さいため地球は動かないとしてよい。さらに, 地球と人工衛星の大きさは無視してよいものとする。
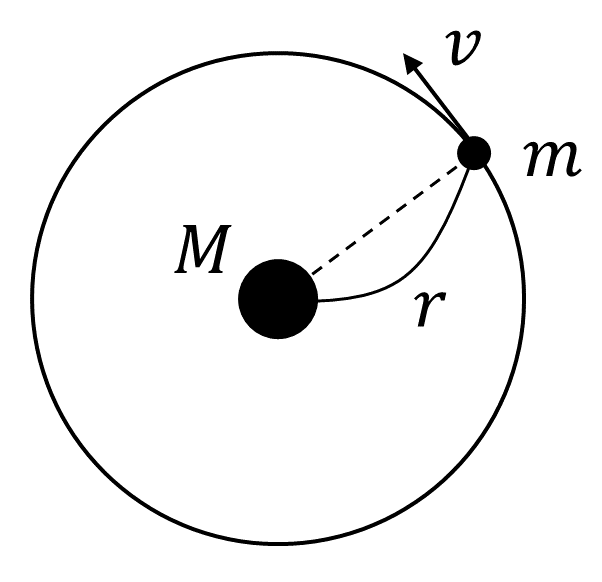
まず, 空気の抵抗力がはたらいていないとする。人工衛星は速さ\( v \), 半径\( r \)の等速円運動をしている。万有引力定数を\( G \)とすると運動方程式は\( \frac{mv^2}{r} = \frac{GMm}{r^2} \)となる。また, 万有引力による位置エネルギーは\( V = -\frac{GMm}{r} \)であることが知られている。このとき運動方程式から, 運動エネルギー\( K \)と位置エネルギー\( V \)との関係式{コ:①\( K = V \) ②\( K = -V \) ③\( 2K = V \) ④\( 2K = -V \) ⑤\( K = 2V \) ⑥\( K = -2V \)}が得られる。
次に, (2), (3)における摩擦力と同様に人工衛星に空気の抵抗力が作用した場合を考える。ここで空気の抵抗力は, 速度と逆方向にはたらく, 大きさ\( D \)の一定の力として取り扱う。ただし, 空気の抵抗力は非常に小さく, 人工衛星は近似的に円運動しているとみなしてよいものとする。
問1
人工衛星の場合にも, (2)と同様に, 運動エネルギーの微小な変化\( \varDelta K \)は万有引力と空気の抵抗力による仕事で与えられる。このことから, 人工衛星の力学的エネルギーの微小な変化\( \varDelta E \)に対して式(i)が成り立つことを, 計算過程も含めて示しなさい。ただし, 半径が\( r \)から\( r – \varDelta r \)に変化するとき, 位置エネルギー\( V = -\frac{GMm}{r} \)の微小な変化は
\( \displaystyle \varDelta V = \varDelta \left( -\frac{GMm}{r} \right) = -GMm\left( \frac{1}{r – \varDelta r} – \frac{1}{r} \right) \fallingdotseq -\frac{GMm}{r^2}\varDelta r \)
という近似式で与えられる。
問2
上の問1の結果と, 微小な変化\( \varDelta K, \varDelta V \)に対しても関係式コと同じ関係が成り立つことを用いて, 式(iii)に対応する人工衛星の速さ\( v \)の変化率を表す方程式を計算過程も含めて導きなさい。また抵抗力により, 人工衛星が加速されるか, 減速されるか, 変化しないか, いずれかであるかを, その理由とともに答えなさい。
解説
(1)
省略。
(2)
ウ
「運動エネルギーの変化 = 外力のした仕事」の関係が成り立つ。今回, 外力は, ばねの力と摩擦力の2種類。ばねの力のうち運動方向に平行な成分は\( br \cos \alpha \)で, 運動方向の向きであるから仕事は正。摩擦力は運動方向と平行で, 逆向きであるから仕事は負。
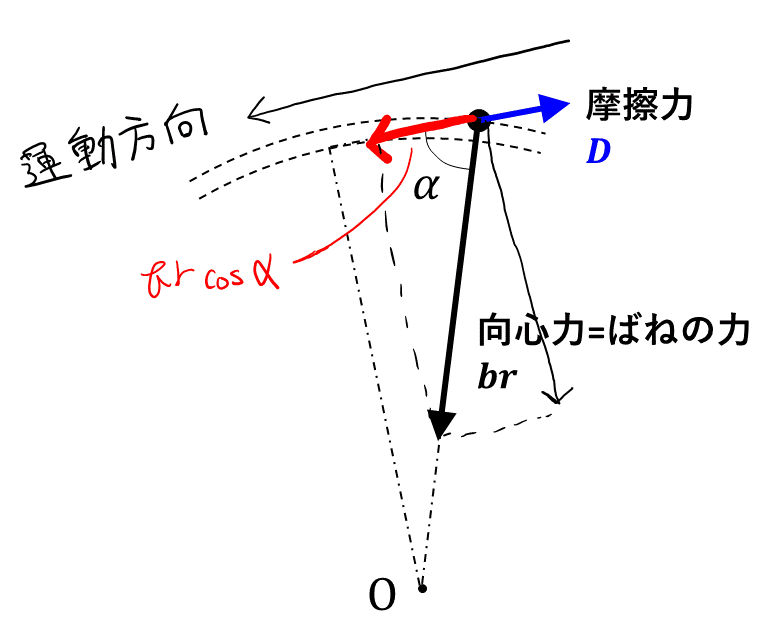
エ
ウでも考えた通り, ばねによる仕事は, \( br \cos \alpha \times \varDelta s \)。ここに, 与えられた式\( \varDelta s \cos \alpha = \varDelta r \)を使うと終了。
オ
ここまでをまとめると以下のようになる。

あとは文中の式\( \varDelta V = -br \varDelta r \)と見比べればOK。
カ
これまで求めた\( -D \varDelta s \)に, 図2中の式\( \varDelta s = v \varDelta t \)を代入するだけ。
キ
まず(i)の等式の成立を確認しておく。ここまでの話で, 「運動エネルギーの変化 = 外力のした仕事」の式は以下のように書き換えられる。

よって, 確かに\( \varDelta E = \varDelta K + \varDelta V \)は, \( \varDelta V \)が相殺されて, \( \varDelta E = -DV \varDelta t \)…(i)となる。
さて, (ii)式は, \( \varDelta K = \)キ\( \times \varDelta E \)という形になっているので, \( K \)(運動エネルギー)と\( E \)(力学的エネルギー)の関係を求めればよい。関係式イの\( K = V \)は使って良いと言われていて, また当然\( E = K + V \)も成り立つので, 2式から\( V \)を消去すると, \( K = \frac{1}{2}E \)。よって\( \varDelta K = \frac{1}{2} \varDelta E \)。
(3)
ここまで出来ていれば簡単なので省略。念のため, \( \frac{\varDelta v}{\varDelta t} \)は加速度のことである。
(4)
コ
省略。
問1
なるべくこれまでと同様に出来ないかを意識して解いていく。
今回も「運動エネルギーの変化 = 外力のした仕事」は成り立つので, 以下のようになる。

よって, 先ほどと同じように, \( \varDelta E = \varDelta K + \varDelta V \)の計算の際に\( \varDelta V \)が打ち消しあう。
問2
コは\( 2K = -V \)。先ほどは\( K = V \)だったのでここが異なるが, 同様に\( E = K + V \)から\( V \)を消去すると, \( K = -E \)。つまり\( \varDelta K = -\varDelta E \)。
この後も同様に, \( \varDelta K = mv\varDelta v \)と連立して\( v \)の変化率(加速度)が求まる。今回は加速度が正となるので, 抵抗力がはたらくにもかかわらず加速されることになる。
コメント