問題
\( m, n \)は自然数で, \( m < n \)をみたすものとする。\( m^n + 1, n^m + 1 \)がともに\( 10 \)の倍数となる\( m, n \)を\( 1 \)組与えよ。
発想
どんな手段でもとにかく\( 1 \)組見つければよいので, 直感的に試してみて, うまく行けばラッキー。直感が働かない場合はいつも通り実験するが, 指数があり計算が大変そうなので, 工夫して楽に計算する必要があるかもしれない。\(10\)の倍数だから, \( \text{mod} 10 \)で合同式も思い浮かぶだろう。
下書き
以下では, 一番回り道だが確実な方法で発見する。いろいろ実験しているうちにひらめくこともあるはずなので, 解説が回りくどい場合は適宜飛ばして, 振り返りをよく読んでほしい。
小さい数字で実験
まずは実験していくが, \( m^n + 1 \)と\( n^m + 1 \)を同時に考えるのは大変そうなので, まず\( m^n + 1 \)が\(10\)の倍数になる\( m, n \)を探し, その中で, \( n^m + 1 \)も\(10\)の倍数になるものを探す。
さらに, \( m^n + 1 \)は普通に計算すると大変すぎるので, 「\( m^n + 1 \)が\(10\)の倍数」\( \Leftrightarrow \)「\( m^n \)は\(10\)で割ると\(9\)余る」\( \Leftrightarrow \)「\( m^n \equiv 9 \pmod{10} \)」と言い換えておく。
なお, 以下の下書き中では\( \pmod{10} \)は省略する。
\( m < n \)の範囲の具体的な数字で実験した結果(途中まで)は以下の通り。
| \( m^n \) | \(m=1\) | \(m=2\) | \(m=3\) | \( \cdots \) |
| \(n=2\) | \(1^2=1\) | \( (m \geqq n) \) | \( (m \geqq n) \) | |
| \(n=3\) | \(1^3=1\) | \(2^3=8\) | \( (m \geqq n) \) | |
| \(n=4\) | \( \cdots \) | \(2^4\equiv8\cdot2\equiv6\) | \(3^4=81\equiv1\) | |
| \(n=5\) | \( \cdots \) | \(2^5\equiv6\cdot2\equiv2\) | \(3^5\equiv1\cdot3\equiv3\) | |
| \(n=6\) | \( \cdots \) | \(2^6\equiv2\cdot2\equiv4\) | \(3^6\equiv3\cdot3\equiv\color{red}{9}\) | |
| \(n=7\) | \( \cdots \) | \(2^7\equiv4\cdot2\equiv8\) | \(3^7\equiv9\cdot3\equiv7\) | |
| \(n=8\) | \( \cdots \) | \( \cdots \) | \(3^8\equiv7\cdot3\equiv1\) | |
| \( \cdots \) |
剰余は循環するので, 循環したところで止めてある。また, \( m^n \equiv \color{red}{9} \)を満たす組が見つかったので, いったんここまでで考えてみる。
\( m=3 \)のとき
周期は\( 4(1\to3\to9\to7) \)であり, \( n=6 \)で\( \equiv\color{red}{9} \)になるので, 一般化すると, \( n = 4k+2(k=1, 2, \cdots) \)のときに\( \equiv\color{red}{9} \)になる。実際に,
\begin{eqnarray}
m^n &=& 3^{4k+2} = 3^2 \cdot 3^{4k} \\
&=& 9 \cdot (3^4)^k = 9 \cdot \color{blue}{81}^k \\
&\color{blue}{\equiv}& 9 \cdot \color{blue}{1}^k = 9
\end{eqnarray}
となることから確かめられる。
ここで逆に, \( n^m \)を考える。これが\( \equiv9 \)になれば, 万事解決である。
\begin{eqnarray}
n^m &=& (4k+2)^3 \\
&=& 64k^3 + 96k^2 + 48k + 8 \\
&\equiv& 4k^3 + 6k^2 + 8k + 8
\end{eqnarray}
は, \( \equiv9 \)になるだろうか。少し考えれば, あり得ないことが分かる。どう考えても偶数なので, \(10\)で割って\(9\)余ることは無い。
一般化して実験
さて, やり直しで, もう一度\( m^n \)から考える必要がある。
先の実験では, \( m, n \)に具体的な数字を入れたが, \(10\)の剰余系で考えているので, \( m \)も最初から剰余で場合分けすれば, 実験の表は(\( n \)の繰り返しを考慮すれば)高々有限の表になることが分かるだろう。
\( m^n \)の表を一気に作り上げてしまう。\( m\equiv1,2,3 \)の場合は先にやったように不適で, \( m\equiv0 \)のときも明らかに不適なので省略すると, 表は以下のようになる。先ほどの表と違い, \( m \)のところが\( = \)ではなく\( \color{blue}{\equiv} \)になっている点に注意。また, \( m < n \)の条件も剰余系ではあまり意味をなさないので考慮していない。
| \( m^n \) | \(m\color{blue}{\equiv}4\) | \(m\color{blue}{\equiv}5\) | \(m\color{blue}{\equiv}6\) | \(m\color{blue}{\equiv}7\) | \(m\color{blue}{\equiv}8\) | \(m\color{blue}{\equiv}9\) |
| \(n=1\) | \(4^1= 4\) | \(5^1= 5\) | \(6^1= 6\) | \(7^1= 7\) | \(8^1= 8\) | \(9^1=\color{red}{9}\) |
| \(n=2\) | \(4^2\equiv4\cdot4\equiv6\) | \(5^2\equiv5\cdot5\equiv5\) | \(6^2\equiv6\cdot6\equiv6\) | \(7^2\equiv7\cdot7\equiv\color{red}{9}\) | \(8^2\equiv8\cdot8\equiv4\) | \(9^2\equiv9\cdot9\equiv1\) |
| \(n=3\) | \(4^3\equiv6\cdot4\equiv4\) | \( \cdots \) | \( \cdots \) | \(7^3\equiv9\cdot7\equiv3\) | \(8^3\equiv4\cdot8\equiv2\) | \(9^3\equiv1\cdot9\equiv9\) |
| \(n=4\) | \( \cdots \) | \( \cdots \) | \( \cdots \) | \(7^4\equiv3\cdot7\equiv1\) | \(8^4\equiv2\cdot8\equiv6\) | \( \cdots \) |
| \(n=5\) | \( \cdots \) | \( \cdots \) | \( \cdots \) | \(7^5\equiv1\cdot7\equiv7\) | \(8^5\equiv6\cdot8\equiv8\) | \( \cdots \) |
| \(n=6\) | \( \cdots \) | \( \cdots \) | \( \cdots \) | \( \cdots \) | \( \cdots \) | \( \cdots \) |
表より, \( m^n \equiv\color{red}{9} \)になる条件が\( 2 \)つ見つかったので, 順に調べていく。運よく\( 1 \)つ目で\( n^m \)も\( \equiv9 \)になるようにできれば, その時点で終了。
\(m\equiv7\)のとき
周期は\( 4(7\to9\to3\to1) \)であり, \( n=2 \)で\( \equiv9 \)になるので, 一般化すると, \( n = 4k+2(k=0, 1, \cdots) \)のときに\( \equiv9 \)になる。
逆に\( n^m \)を考えると, \( n^m = (4k+2)^7 \)は, 先ほどと同様に必ず偶数なので, \(10\)で割って\(9\)余ることは無い。失敗。
\(m\equiv9\)のとき
周期は\( 2(9\to1) \)であり, \( n=1 \)で\( \equiv9 \)になるので, 一般化すると, \( n = 2k+1(k=0, 1, \cdots) \)のときに\( \equiv9 \)になる。
逆に\( n^m \)を考えると, \( n^m = (2k+1)^9 \)が\( \equiv9 \)になればよい。というより, もうこれしか残っていないので, 必ず\( \equiv9 \)になるように出来るはずである。ということで頑張って探すと, \( k = 4 \)のとき, \( \text{mod} \)をうまく使って,
$$(2k+1)^9 = 9^9 \equiv (-1)^9 = -1 \equiv 9$$
と出来ることに気付く。これが答えである。
(必ず答えが見つかることは確定しているので, \( 3^9, 5^9, 7^9, \cdots \)を順番に, 頑張って手計算で調べて行ってもよい。余りさえ見ればよいので, 案外楽に調べられる。)
別に\( 9^9 \)に限らず, \( 19^9 \)でも\( 29^9 \)でも同様に式変形できる。つまり, \( m \equiv 9, n \equiv 9 \)のとき, \( m^n \equiv 9, n^m \equiv 9 \)となるようである。あとは\( m < n \)に気を付けて適当に答えればよい。
解答例
\( m=9, n=9999 \)とする。このとき,
\begin{align}
&m^n + 1 = 9^{9999} + 1 \equiv (-1)^{9999} + 1 = -1 + 1 = 0 \pmod{10}, \\
&n^m + 1 = 9999^{9} + 1 \equiv (-1)^{9} + 1 = -1 + 1 = 0 \pmod{10}
\end{align}
より, \( m^n + 1, n^m + 1 \)はともに\( 10 \)の倍数である。
よって, 題意を満たす\( m, n \)の組の一つは, \( m=9, n=9999 \)
振り返り
偶奇で絞り込み
偶奇に着目する姿勢があると, \( m^n + 1, n^m + 1 \)がともに\(10\)の倍数, つまり偶数になるには, \( m^n, n^m \)がともに奇数でないといけないことに気付く。\( (m, n) = \) (偶, 偶), (偶, 奇), (奇, 偶), (奇, 奇)の\( 2 \times 2 = 4 \)パターンを調べると, \( m, n \)はともに奇数の場合しかありえないことが分かる。
奇数だと分かれば, 実は\( m^n + 1 \)は因数分解できる。
\(n\)乗の差の因数分解公式は常識だが, \(n\)乗の和の因数分解公式はあまり知られていない。(使う機会がないので無理に覚えなくてもよいが, \( x^3+y^3 = (x+y)(x^2-xy+y^2) \)の一般化であることを意識すれば, 容易に覚えられる。)
\( n \)が自然数のとき,
\begin{eqnarray}
x^n – y^n = (x-y)(x^{n-1} + x^{n-2}y + \cdots + xy^{n-2} + y^{n-1})
\end{eqnarray}
\( n \)が奇数のときに限り,
\begin{eqnarray}
x^n + y^n = (x+y)(x^{n-1} – x^{n-2}y + \cdots – xy^{n-2} + y^{n-1})
\end{eqnarray}
もしこれを知っていれば,
$$m^n + 1 = (m+1)(m^{n-1} – m^{n-2} + \cdots – m + 1)$$
と因数分解できるので, これが\(10\)の倍数になるには, \( m \)の\(1\)の位が\(9\)であればよいことがすぐにわかる(\(n\)も同様)。
もっとシンプルに絞り込み
また, 特に偶奇や\( \rm{mod} \)を意識しなくても, そもそも累乗して\(1\)の位が\(9\)になり得るのは, \(3, 7, 9\)に限られる。
整数問題では, このような絞り込みが出来れば, 素早く解くことができる。解説のように, しらみつぶしでも最悪解ける問題なので, 必ず確保したい問題である。
補足
「\( m \equiv 9 \)かつ\( n \equiv 9 \)」は, 「\( m^n \equiv 9 \)かつ\( n^n \equiv 9 \)」の必要十分条件(つまり, 逆も成り立つ)である。解説でほとんど示されているが, 興味がある人は証明を書き上げてみてほしい。更に意欲がある人は, \( \text{mod} 10 \)や\( \equiv 9 \)の, \( 10 \)や\( 9 \)を一般化するとどうなるか, 考えてみるのも良いだろう。
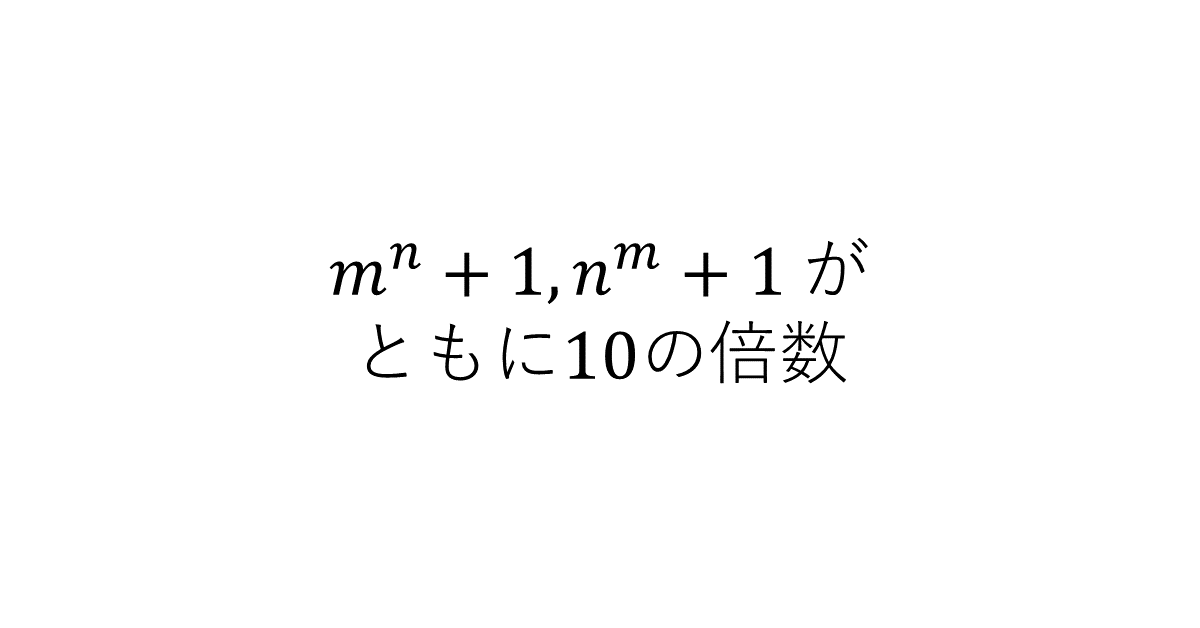
コメント