問題
\( n \)を自然数とし, 整式\( x^n \)を整式\( x^2 – 2x – 1 \)で割った余りを\( ax + b \)とする。このとき\( a \)と\( b \)は整数であり, さらにそれらをともに割り切る素数は存在しないことを示せ。
発想
多項式の割り算なので, \( \alpha^n = a \alpha + b, \beta^n = a \beta + b \)までは一本道だが, そこからが難しい。そのまましばらく計算を続けるか, 一度立ち止まって考える。
下書き
\( x^n = (x^2 – 2x -1) Q(x) + ax + b \)とおき, \( x^2 – 2x – 1 = 0 \)の解を\( x = \alpha, \beta \)とする\( ( \alpha = 1+\sqrt{2}, \beta = 1-\sqrt{2} ) \)。
\( x = \alpha, \beta \)を代入して, \( \alpha^n = a \alpha + b, \beta^n = a \beta + b \)。
ここから, 連立方程式を解いて\( a, b \)を求めればよい。
\( a = \frac{\alpha^n – \beta^n}{\alpha – \beta} = \alpha^{n-1} + \alpha^{n-2}\beta + \cdots + \beta^{n-1} \)はすぐに求まるが, これが整数と言うのは少し難しそう。
ここで, 一旦立ち止まるか, ゴリゴリ計算を進めるか, 分かれる。
問題文に立ち返る
いったん問題文を冷静に読み直してみる。
よく考えると, 整式\( x^n \)を整式\( x^2 – 2x – 1 \)で割った余りは, \( n \)によるので, \( ax + b \)ではなく, \( a_n x + b_n \)とおくのが普通であろう。よって, \( x^n = (x^2 – 2x -1) Q_n(x) + a_nx + b_n \)とおいて, 漸化式を立ててみる。
漸化式を立てる
\( x^n = (x^2 – 2x -1) Q_n(x) + a_nx + b_n \)
の両辺に\( x \)をかけて, \( x^2 – 2x -1 \)でくくることを意識して変形すると,
$$\begin{eqnarray}
x^{n+1} &=& x(x^2-2x-1)Q_n(x) + \underline{a_n x^2} + b_n x \\
&=& (x^2-2x-1)xQ_n(x) + \underline{a_n(x^2-2x-1) + 2a_n x + a_n} + b_n x \\
&=& (x^2-2x-1)(xQ_n(x) + a_n) + (2a_n + b_n)x + a_n \\
&=& (x^2-2x-1)Q_{n+1}(x) + a_{n+1}x + b_{n+1}
\end{eqnarray}$$
よって, \( a_{n+1} = 2a_n + b_n, b_{n+1} = a_n \)。
これは解かなくても, \( a_1 = 1, b_1 = 0 \)から, 帰納的に, 全ての\( n \)で\( a_n, b_n \)は整数であることが直ちに分かる。
割り切る素数が無いことを示す
あとは, すべての\( n \)について, \( a_n, b_n \)を共に割り切る素数はないことを示せばよい。すべての\( n \)についての命題なので, 帰納法が第一候補。
\( a_k, b_k \)を共に割り切る素数はない, と仮定し, その仮定の下で, \( a_{k+1}, b_{k+1} \)を共に割り切る素数もないことを示す。
今使える条件は, \( a_{k+1} = 2a_k + b_k\)…①, \( b_{k+1} = a_k \)…②と, \( a_k, b_k \)を共に割り切る素数はない…③, ということだけである。ここから進めるには, 「背理法」が必要だとたどり着いてほしい。
\( a_{k+1}, b_{k+1} \)を共に割り切る素数が「ある」とすると, \( a_{k+1} = pA, b_{k+1} = pB \)と書ける素数\( p \), 整数\( A, B \)があることになる。よって, \( a_{k+1} = 2a_k + b_k\)①, \( b_{k+1} = a_k \)②は, \( pA = 2a_k + b_k \)…④, \( pB = a_k \)…⑤となる。
ここで, \( pB = a_k \)⑤→\( pA = 2a_k + b_k \)④の順にみると, \( a_k \)は\( p \)の倍数で, \( b_k \)も\( p \)の倍数になってしまうが, これは\( a_k, b_k \)を共に割り切る素数はない③に反する。よって, \( a_{k+1}, b_{k+1} \)を共に割り切る素数は「ない」。
これで帰納法が完成し, 満点をもらえる。
ゴリゴリ計算を進める
\( a \)が整数を示す
\( \alpha^n = a \alpha + b, \beta^n = a \beta + b \)より, \( a = \frac{\alpha^n – \beta^n}{\alpha – \beta} \)と求めていた。まずこれが整数であることを頑張って示す。
\( \alpha, \beta \)のままだと, \( \alpha^n – \beta^n \)の漸化式を立てないといけなかったりして大変であるが, せっかく\( \alpha, \beta \)は求まっているので具体的に代入して, \( a = \frac{(1+\sqrt{2})^n – (1-\sqrt{2})^n}{2\sqrt{2}} \)となる。こうすると, 何となくうまく相殺されて整数になりそう(\( n=2, 3 \)などで試してみるとよい)。
分子を具体的に計算してみると,
$$\begin{eqnarray}
(1+\sqrt{2})^n – (1-\sqrt{2})^n
&=& \displaystyle\sum_{k=0}^n {}_nC_k (\sqrt{2})^k – \sum_{k=0}^n {}_nC_k (-\sqrt{2})^k \\
&=& \sum_{k=0}^n {}_nC_k \left((\sqrt{2})^k – (-\sqrt{2})^k\right)
\end{eqnarray}$$
シグマの中身に注目すると, \( k \)が偶数なら\( 0 \)になるので無視してよく, \( k \)が奇数なら, \( {}_nC_k \cdot 2 (\sqrt{2})^k \)となるので, \( 2\sqrt{2} \)の倍数となる。
よって, \( a = \frac{(1+\sqrt{2})^n – (1-\sqrt{2})^n}{2\sqrt{2}} \)は整数となる。
\( b \)が整数を示す
次に, \( b \)が整数であることを示す。
\( \alpha^n = a \alpha + b, \beta^n = a \beta + b \)より, 今度は\( a \)を消去すると, 多少の計算により, \( b = \frac{(1+\sqrt{2})^{n-1} – (1-\sqrt{2})^{n-1}}{2\sqrt{2}} \)となる。
これは, \( a \)とほとんど同じで, \( n \)が\( n-1 \)になっただけなので, 上と同様に\( b \)も整数であることが示せる。
割り切る素数が無いことを示す
最後に, \( a \)と\( b \)を共に割り切る素数は存在しないことを示す。
ここまでで求めた\( a, b \)は, ややこしい形をしているので, それらを直接使って示すのは難しく, 趣の異なるアプローチが必要。以下は普通は思いつかないので, この方法ではここまでできれば十分。
\( \alpha^n = a \alpha + b, \beta^n = a \beta + b \)を辺々掛けると, \( (\alpha \beta)^n = a^2\alpha \beta + ab(\alpha + \beta) + b^2 \)すなわち\( (-1)^n = -a^2 + 2ab + b^2 \)…⑥となる。
ここで, \( a \)と\( b \)を共に割り切る素数が「ある」と仮定し, その素数を\( p \)とすると, \( (-1)^n = -a^2 + 2ab + b^2 \)⑥の右辺は\( p \)の倍数であるが, 左辺は明らかに\( p \)の倍数でないので, 矛盾。
よって, \( a \)と\( b \)を共に割り切る素数は「ない」。
解答例
\( x^n \)を\( x^2 – 2x – 1 \)で割った商を\( Q_n(x) \), 余りを\( a_n x + b_n \)とおくと,
\begin{align}
&x^1 = (x^2 – 2x -1) Q_1(x) + a_1x + b_1 \cdots ① \\
&x^n = (x^2 – 2x -1) Q_n(x) + a_nx + b_n \cdots ② \\
&x^{n+1} = (x^2 – 2x -1) Q_{n+1}(x) + a_{n+1}x + b_{n+1} \cdots ③
\end{align}
\( x^n = (x^2 – 2x -1) Q_n(x) + a_nx + b_n \)②の両辺に\( x \)をかけて,
$$\begin{eqnarray}
x^{n+1} &=& x(x^2 – 2x -1) Q_n(x) + a_nx^2 + b_n x \\
&=& (x^2-2x-1)(Q_n(x)x + a_n) + (2a_n + b_n)x + a_n
\end{eqnarray}$$
\( x^{n+1} = (x^2 – 2x -1) Q_{n+1}(x) + a_{n+1}x + b_{n+1} \)③と係数比較すると, \( a_{n+1} = 2a_n + b_n, b_{n+1} = a_n \)…④となり, これは任意の自然数\( n \)で成り立つ。
ここで, \( x^1 = (x^2 – 2x -1) \cdot 0 + 1 \cdot x + 0 \)より, \( x^1 = (x^2 – 2x -1) Q_1(x) + a_1x + b_1 \)①と係数比較して, \( a_1 = 1, b_1 = 0 \)である。
以下, 任意の自然数\( n \)について, \( P(n) \):「\( a_n, b_n \)は整数であり, かつそれらを共に割り切る素数は存在しない」ということを, \( n \)に関する数学的帰納法で示す。
(i) \( a_1 = 1, b_1 = 0 \)より, \( a_1, b_1 \)は整数で, それらを共に割り切る素数は存在しないので, \( P(1) \)は成り立つ。
(ii) \( P(k) \)が成り立つと仮定する。
\( a_{n+1} = 2a_n + b_n, b_{n+1} = a_n \)④より, \( a_{k+1} = 2a_k + b_k, b_{k+1} = a_k \)となるが, \( P(k) \)の仮定より\( a_k, b_k \)は整数なので, \( a_{k+1}, b_{k+1} \)も整数である。
ここで, さらに, 「\( a_{k+1}, b_{k+1} \)を共に割り切る素数が存在する」…⑤と仮定し, 矛盾を導く。
その素数を\( p \)とすると,
\( a_k = b_{k+1} \)より, \( a_k \)は\( p \)の倍数
\( b_k = a_{k+1} – 2a_k \)より, \( b_k \)は\( p \)の倍数
となるが, これは, \( P(k) \)の仮定, すなわち, \( a_k, b_k \)を共に割り切る素数が存在しないという仮定に反する。
よって, \( a_{k+1}, b_{k+1} \)を共に割り切る素数が存在する⑤の仮定は誤りであり, \( a_{k+1}, b_{k+1} \)を共に割り切る素数は存在しない。
以上より, \( P(k) \)の仮定の下で, \( P(k+1) \)が成り立つ。
したがって, (i)(ii)より, \( n \)がどんな自然数であっても, \( a \)と\( b \)は整数であり, さらにそれらをともに割り切る素数は存在しない。
振り返り
多項式の割り算の原則に従って計算を進めると, 行き詰まってしまう。
余りを漸化式で表す問題は, 京大含めて多くの大学で出題されており, パターンといえばパターンなので, やったことがある人はいつもの調子で解けたかもしれない。しかし, 問題文からは漸化式が読み取れないので, ほとんどの受験生は漸化式の発想が出なかったと思われる。その場合は, \( a, b \)が整数までは示しておきたいところ。
漸化式が出たあとはよくある流れだと言えるが, それでも帰納法の中でさらに背理法を使うなど, 論理的に多少難しい部分を含んでおり, 全体としては難問である。
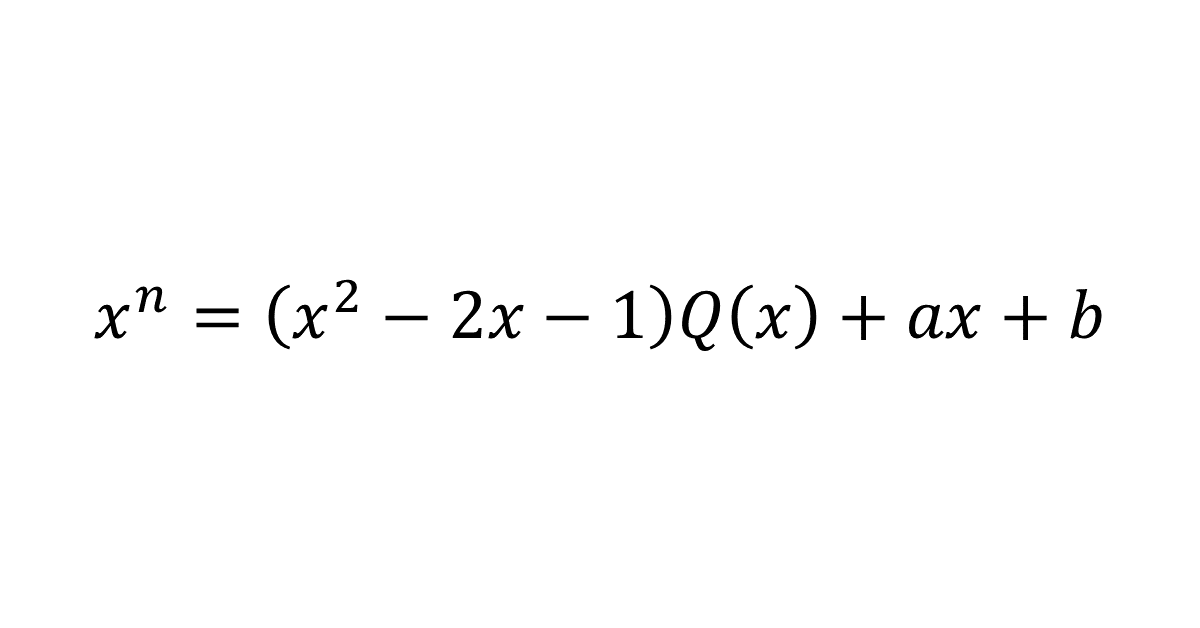
コメント