問題
\( \frac{2^n}{n} > n \)を満たす自然数\( n \)の範囲を求めよ。
発想
まずは実験する。指数は多項式と比べて発散することを意識すると, 傾向はすぐにわかるはず。
下書き
自然数\( n \)の範囲では, \( \frac{2^n}{n} > n \Leftrightarrow 2^n > n^2 \)なので, こちらで考える。
| \( n \) | \( 1 \) | \( 2 \) | \( 3 \) | \( 4 \) | \( 5 \) | \( 6 \) | \( 7 \) | \( \cdots \) |
| \( 2^n \) | \( 2 \) | \( 4 \) | \( 8 \) | \( 16 \) | \( 32 \) | \( 64 \) | \( 128 \) | \( \cdots \) |
| \( n^2 \) | \( 1 \) | \( 4 \) | \( 9 \) | \( 16 \) | \( 25 \) | \( 36 \) | \( 49 \) | \( \cdots \) |
発散の大きさを考慮すると, \( n \geqq 5 \)以降はずっと\( 2^n > n^2 \)と予測できるので, それを示す。自然数の命題なので帰納法が第一候補で, 実際にそれで問題なく示せる。
(i) \( n = 5 \)のとき, 上の実験より, 成り立つ。
(ii) \( n = k \)のとき, \( \color{red}{2^k > k^2} \)と仮定して, \( 2^{k+1} > (k+1)^2 \)を示す。
これを示すために(左辺)\( – \)(右辺)をし, 仮定を利用するために\( 2^{k+1} \)を\( 2 \cdot \color{red}{2^k} \)と分解すると,
\begin{eqnarray}
2^{k+1} – (k+1)^2 = 2 \cdot \color{red}{2^k} – (k+1)^2 \color{red}{>} 2 \cdot \color{red}{k^2} – (k+1)^2
\end{eqnarray}
ただの二次式になったので, 平方完成して\( 0 \)以上を示せばよい。
\( 2 k^2 – (k+1)^2 = (k-1)^2 – 2 \)は, 今\(k \geqq 5 \)の範囲で考えているので, \( > 0 \)が言えて, \( 2^{k+1} > (k+1)^2 \)となる。
(i)(ii)より, \( n \geqq 5 \)では\( \frac{2^n}{n} > n \)を満たすので, 実験と合わせて, 求める\( n \)の範囲は, \( n = 1, n \geqq 5 \)。
解答例1
\( n \)が自然数のとき, \( \frac{2^n}{n} > n \Leftrightarrow 2^n > n^2 \)となる。
\( n = 1 \)のとき, \( 2^n > n^2 \)は成り立つ。
\( n = 2, 3, 4 \)のとき, \( 2^n > n^2 \)は成り立たない。
\( n \)に関する命題\( P(n) \)を, \( P(n) : \)「\( 2^n > n^2 \)である」とおき, \( n = 5, 6, \cdots \)のときに\( P(n) \)が成り立つことを, \(n\)に関する数学的帰納法で示す。
(i) \(n=5\)のとき, \( P(5) \)は成り立つ。
(ii) \( n=k(k=6,7,\cdots) \)のとき, \( P(k) \)が成り立つと仮定する。\( n = k+1 \)のときを考えて,
\begin{eqnarray}
2^{k+1} – (k+1)^2 &>& 2k^2 – (k+1)^2 (\because P(k)) \\
&=& (k-1)^2 – 2 > 0 (\because k \geqq 6)
\end{eqnarray}
より, \( P(k+1) \)も成り立つ。
(i)(ii)より, \( n = 5, 6, \cdots \)のときに\( P(n) \)が成り立つことが示された。
よって, 求める自然数\( n \)の範囲は, \( n=1, n \geqq 5 \)。
発想2
\( 2^n > n^2 \)を見たときに, 理系であれば, 微分を思いついてほしい。典型問題として, \( e^\pi \)と\( \pi^e \)の大小を比べる問題がある。これは,
\begin{eqnarray}
e^\pi \gtrless \pi^e &\Leftrightarrow& \log e^\pi \gtrless \log \pi^e \\
&\Leftrightarrow& \pi \log e \gtrless e \log \pi \\
&\Leftrightarrow& \frac{\log e}{e} \gtrless \frac{\log \pi}{\pi}
\end{eqnarray}
(※ \( \gtrless \)は\( \pm \)の複合同順みたいなイメージ)
と変形して, \( f(x) = \frac{\log x}{x} \)の増減を調べることで, \( f(e) \)と\( f(\pi) \)を比べることができる。
本問も同様に変形して, \( f(2) \)と\( f(n) \)を比べればよい。
解答例2
\( f(n) = \frac{\log n}{n} (n \geqq 1) \)とおく。
\( f'(n) = \frac{1 – \log n}{n^2} \)より, 増減表は以下のようになる。
| \( n \) | \(1\) | \(\cdots\) | \(e\) | \(\cdots\) |
| \( f'(n) \) | \(+\) | \(+\) | \(0\) | \(-\) |
| \( f(n) \) | \(0\) | \( \nearrow \) | \( \frac{1}{e} \) | \( \searrow \) |
\( f(2) = \frac{\log 2}{2}, \) \( f(4) = \frac{\log 2}{2} = f(2), \) \( \displaystyle\lim_{n \to \infty}f(n) = 0 \)を考慮すると, グラフは以下のようになる。
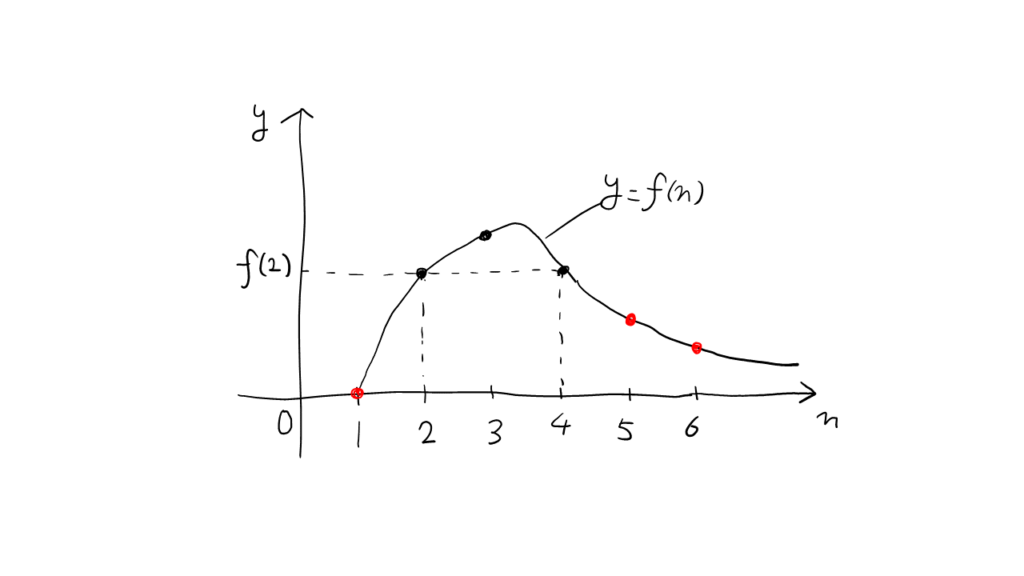
よってグラフより, \( n \)が自然数の範囲では, \( n=1, n \geqq 5 \)の場合に限り, \( \color{red}{f(2) > f(n)} \)が成り立つ。このとき,
\begin{eqnarray}
f(2) > f(n) &\Leftrightarrow& \frac{\log 2}{2} > \frac{\log n}{n} \Leftrightarrow n\log2 > 2\log n \\
&\Leftrightarrow& \log 2^n > \log n^2 \Leftrightarrow 2^n > n^2 \Leftrightarrow \frac{2^n}{n} > n
\end{eqnarray}
であるから, \( \frac{2^n}{n} > n \)を満たす自然数\( n \)の範囲は, \( n=1, n \geqq 5 \)である。
振り返り
かなり平易で, 必ず完答しないといけない問題である。発想2は多少発展的だが, たまに見かけるので, 理系の人は余裕があれば理解しておきたい。
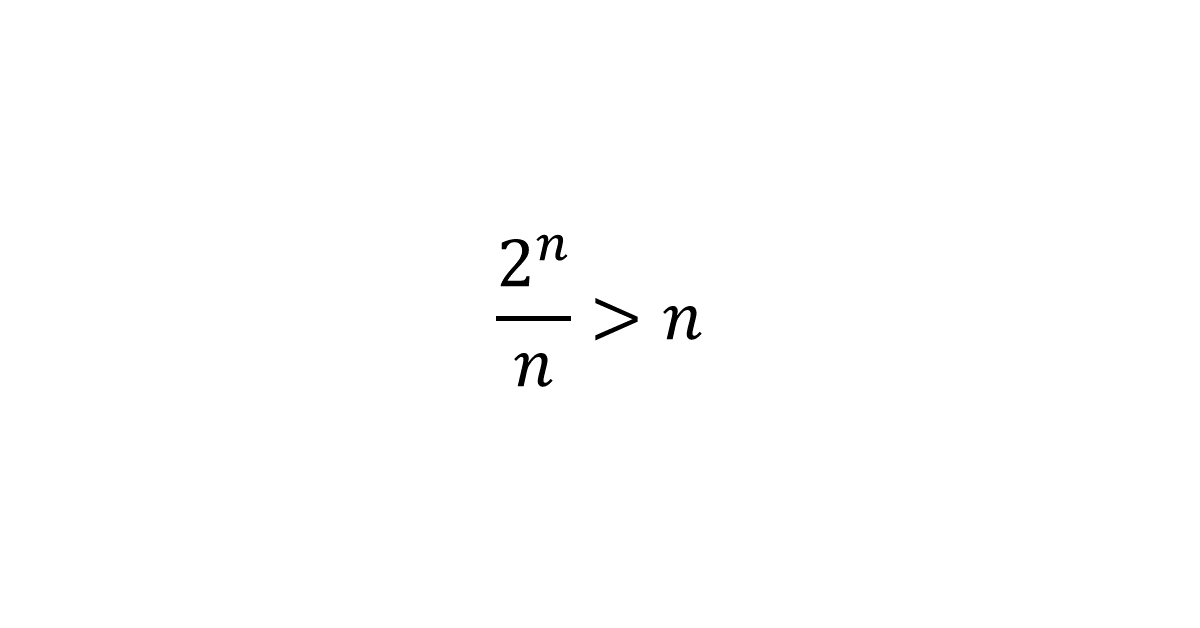
コメント