問題
\( n \)と\( k \)を自然数とし, 整式\( x^n \)を整式\( (x-k)(x-k-1) \)で割った余りを\( ax + b \)とする。
(1) \( a \)と\( b \)は整数であることを示せ。
(2) \( a \)と\( b \)を共に割り切る素数は存在しないことを示せ。
発想
多項式の割り算の原則に従うと(1)は一本道。
(2)は, 存在しないことの証明だから背理法が第一候補。問題文を言い換えると, 共に割り切る素数が存在しないということは, 互いに素であるということなので, 互いに素であることを証明すると考えてもよい。
互いに素を証明するには, 主に以下のパターンが定石である。
①最大公約数を\( d \)とおいて\( d = 1 \)を示す
②素因数\( p \)の存在を仮定して矛盾を導く(背理法)
③ユークリッドの互除法で, 直接最大公約数\( =1 \)を求める
よって, やはり背理法でやるのがよさそう。
下書き
(1)
\( x^n = (x-k)(x-k-1)Q(x) + ax + b \)とおき, \( x = k, k+1 \)を代入すると, \( k^n = ak + b \)…①, \( (k+1)^n = a(k+1) + b \)…②。ここまでは一本道。
\( a, b \)の連立方程式なので, \( a, b \)を具体的に求めることができ, \( a = (k+1)^n – k^n \)…③, \( b = (k+1)k^n – k(k+1)^n \)…④となる。
\( n \)と\( k \)は自然数なので, 直ちに\( a \)と\( b \)も自然数と言える。
(2)
背理法でやってみる。割り切る素数があると仮定し, その素数を\( p \)とおくと, \( a = pA, b = pB \)(\( A, B \)は整数)と書ける。
(1)の流れから, \( a = (k+1)^n – k^n \)③, \( b = (k+1)k^n – k(k+1)^n \)④式を使って, \( (k+1)^n – k^n = pA \), \( (k+1)k^n – k(k+1)^n = pB \)から考えるのが自然。ここから矛盾を導く。
\( (k+1)^n \)が共通しているので, 消去してみると, \( k^n = p(kA + B) \)とシンプルになるが, これ以上どうすることもできない。
ここで, 使えそうな式を改めて見直すと, \( k^n = ak + b \)①, \( (k+1)^n = a(k+1) + b \)②式の\( k^n = \color{red}{a}k + \color{red}{b} \), \( (k+1)^n = \color{red}{a}(k+1) + \color{red}{b} \)がある。仮定(\( a,b \)は\( \color{red}{p} \)の倍数)より, それぞれの右辺は\( p \)の倍数になるので, 左辺も\( p \)の倍数。
すなわち, \( k^n, (k+1)^n \)は\( p \)の倍数。これは矛盾を導けそう。
矛盾を導く方法1
\( p \)は素数だから, \( k^n, (k+1)^n \)が\( p \)の倍数ならば, \( k, k+1 \)も\( p \)の倍数(\( p \)は素数という条件が必ず必要!)。
よって, その差\( k+1-k = 1 \)も\( p \)の倍数であるが, これは明らかに矛盾。
矛盾を導く方法2
連続整数である\( k, k+1 \)は互いに素(常識!)だから, \( k^n, (k+1)^n \)も互いに素。
これは, \( k^n, (k+1)^n \)がともに\( p \)の倍数であることに矛盾。
解答例
(1)
整式\( x^n \)を整式\( (x-k)(x-k-1) \)で割った商を\( Q(x) \)とすると, \( x^n = (x-k)(x-k-1)Q(x) + ax + b \)と書ける。
\( x = k, k+1 \)を代入すると, \( k^n = ak + b \), \( (k+1)^n = a(k+1) + b \)…①
よって, \( a = (k+1)^n – k^n \), \( b = (k+1)k^n – k(k+1)^n \)
\( n \)と\( k \)は自然数だから, \( a \)と\( b \)は整数である。
(2)
\( a \)と\( b \)を共に割り切る素数が存在すると仮定し, その素数を\( p \)とする。
このとき, \( a \)と\( b \)は\( p \)の倍数であるから, \( k^n = ak + b \), \( (k+1)^n = a(k+1) + b \)①より, \( k^n, (k+1)^n \)も\( p \)の倍数である。
ここで, \( p \)は素数であるから, \( k, k+1 \)も\( p \)の倍数となる。
よって, \( k+1-k=1 \)も\( p \)の倍数となるが, これは\( 1 \)が素数の倍数ということになり, 矛盾する。
したがって, \( a \)と\( b \)を共に割り切る素数は存在しない。
振り返り
(1)は基本問題で, 取れないと合格はない。(2)は, 背理法と分かっても, 矛盾を導くところが意外と難しい。どの式を使えばよいかを冷静に見極める必要がある。
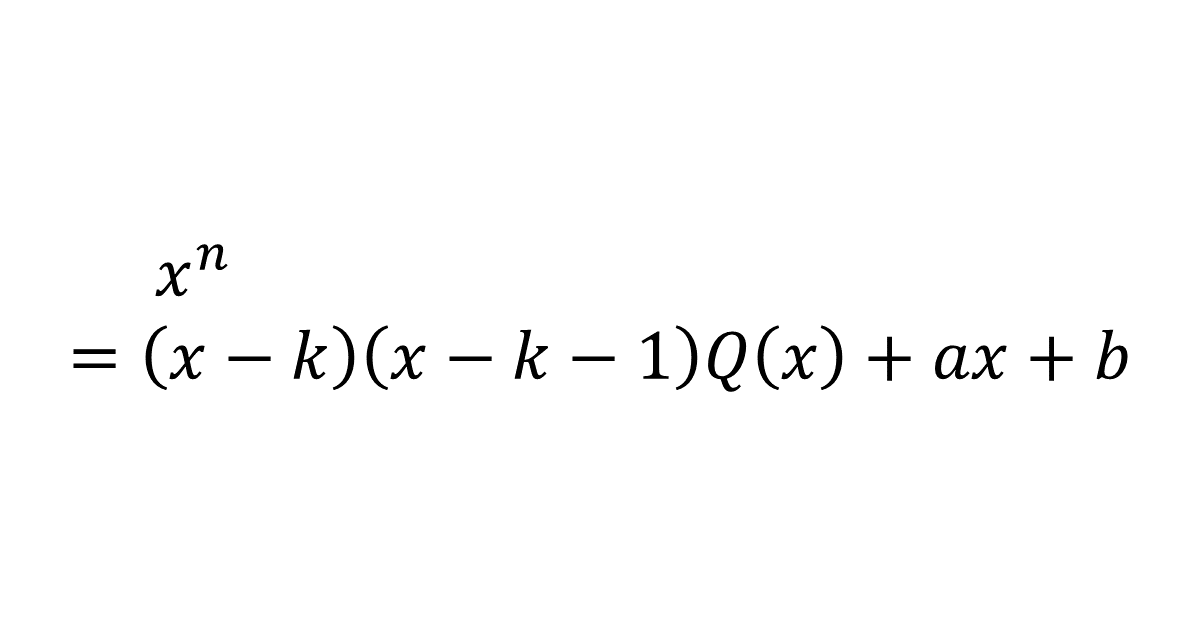
コメント