問題
次の文を読んで には適した式または数をそれぞれの解答欄に記入せよ。なお はすでに で与えられたものと同じものとする。\( L \)ヌの肩にのった小さな は, べきの指数を意味する。{ ハ }には適切な語句を選んで記入せよ。
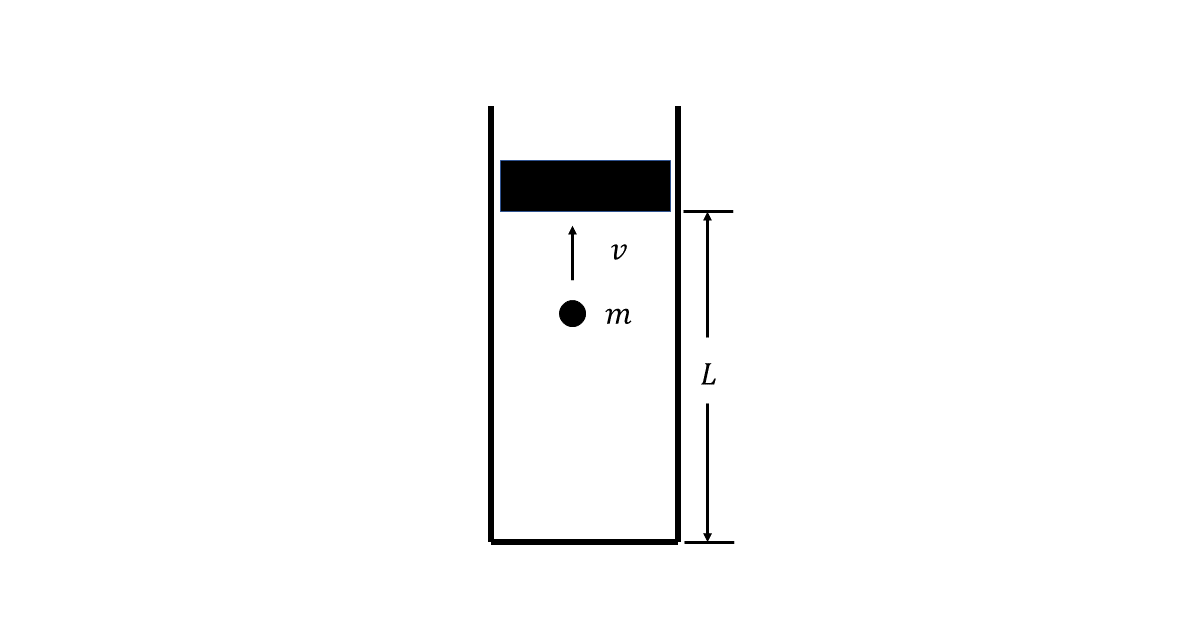
図1のような, 鉛直に立てたシリンダーに平行に, 質量\( m \)の粒子が底の弾性壁と上のピストンの弾性壁との間を往復運動している。ここで, 粒子の運動に関しては重力の効果は無視できるものとする。まず, ピストンが固定されている場合について考えよう。粒子の速さを\( v \), 底面からのピストンの高さを\( L \)とすると, 粒子が上のピストンに衝突する回数は単位時間当たりイである。ピストンが受ける単位時間当たりの力積はロとなる。この単位時間当たりの力積をここでは「圧力」と呼び, \( P \)と表すことにするが, この次元は通常の圧力の次元とは異なり, {ハ:運動量, 力, 速度, 加速度}と同じものである。\( P \)と\( L \)の積は粒子の運動エネルギー\( E \)を用いて\( PL = \)ニと表すことができる。
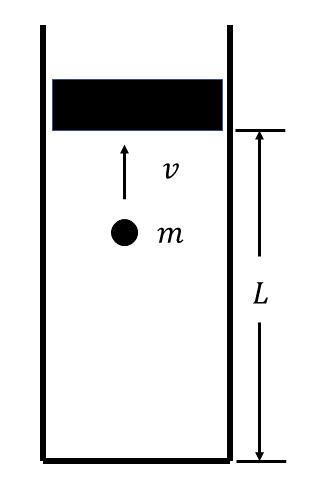
次に, ピストンを一定の速さ\( w \)で押し込むことにする。速さ\( v \)でピストンに衝突した粒子は完全弾性衝突によりホの速さとなる。粒子が反射したときにピストンの高さは\( L \)だったとする。ピストンから反射した速さホの粒子がシリンダーの底で反射して再び移動中のピストンに衝突するまでの往復時間はへである。この粒子が一往復する間にピストンの高さは\( L \)から\( L’ = \)トへと変化し, 粒子の速さは一回の衝突で\( v \)から\( v’ = \)ホへと変化している。粒子の一往復当たりのピストンの高さの比率\( \frac{L’}{L} \)と粒子の速さの比率\( \frac{v’}{v} \)の積\( \frac{L’v’}{Lv} \)は\( x = \frac{w}{v} \)を用いてチと表される。\( |x| \)が\( 1 \)に比べて十分小さい場合には\( (1 + ax)(1 + bx) \)は\( 1 + (a+b)x \)と近似できるので\( \frac{L’v’}{Lv} \)は\( 1 \)となる。よって粒子の速さに比べてゆっくりとピストンを動かす限り粒子の速さ\( v \)と\( L \)の積は一定に保たれる。この結果, ピストンの高さ\( L \)を半分まで押し下げたときには「圧力」\( P \)はもとのリ倍になることがわかる。つまりこの過程では\( PL \)ヌが一定に保たれる。
この仮定では, 粒子の速さはピストンを動かす速さ\( w \)によらず, ピストンの高さ\( L \)によってきまる。このことが成り立つためには, ピストンの速さが粒子の速さに比べて十分小さいという条件が必要である。以下でもこの条件が成り立つものとする。
さて, シリンダーが鉛直におかれているときに, 質量\( M \)のピストンにかかる重力と, 粒子の上下運動による「圧力」が釣り合って, ピストンが底から\( L \)の高さに浮いていたとする。ここで, 粒子の質量はピストンの質量に比べて十分小さく, 粒子が衝突するたびに起こっているピストンの細かな動きは無視するものとする。このピストンを少し押し込んで, 底からの高さを\( L – \Delta \)としたときの「圧力」の増分を求めよう。\( L \)に比べて\( \Delta \)が十分小さい時の「圧力」の増分は\( M \), \( L \), および重力加速度\( g \)を用いて\( \Delta \times \)ルとなる(ここで\( 1 \)に比べて十分小さい\( |x| \)について\( (1-x)^{-a} \)を\( 1 + ax \)とする近似を利用する)。ピストンは摩擦がなければこの復元力によって振動を行う。ばねの単振動から類推すると, このピストンの振動の周期は\( L \)および\( g \)を用いて\( 2\pi \times \)ヲとなることがわかる。
解説
イロ
往復距離\( 2L \)ごとに衝突する。単位時間に粒子は\( v[\rm{m}] \)進むので, 図より衝突回数は割り算すればよいとわかり, \( \frac{v}{2L}[回] \)。
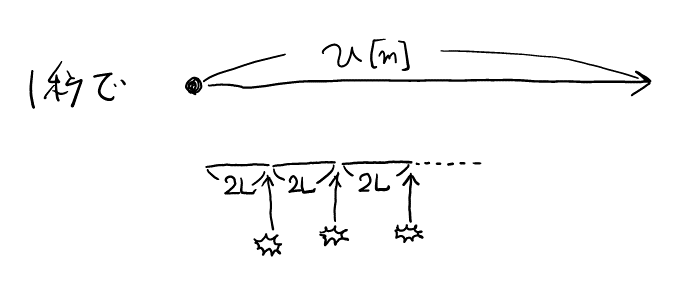
1回の衝突における力積の大きさは, 図を書くまでもなく\( mv – (-mv) \)なので, 単位時間当たりの力積の合計は, 衝突回数をかければよい。
ハ
慣れている人であれば, 近い公式を探して, 力積の公式\( I = F \varDelta t \)より, 単位時間当たりの力積(\( \frac{I}{\varDelta t} \))は, 力と同じであると判断できる。
ここでは, 多少時間はかかるが, 次元を比較してみる。次元は, 長さ\( L[\rm{\color{red}{m}}] \), 時間\( T[\rm{\color{blue}{s}}] \), 質量\( M[\rm{kg}] \)の3要素で表せる。
速度の次元は, \( [\rm{\color{red}{m}/\color{blue}{s}}] \)より\( \underline{LT^{-1}} \)。
加速度の次元は, \( [\rm{m/s^2}] \)より\( LT^{-2} \)。
運動量\( m\underline{v} \)の次元は, \( M(\underline{L/T}) = MLT^{-1} \)。
力の次元は, \( ma = F \)の左辺より, \( M(L/T^2) = MLT^{-2} \)。
\( P = \frac{mv^2}{L} \)の次元は, \( \frac{M(L/T)^2}{L} = MLT^{-2} \)。
ニ
省略。
ホ
速度の向きが明らかなので, 速さを未知数として, はねかえりの式を立てる。
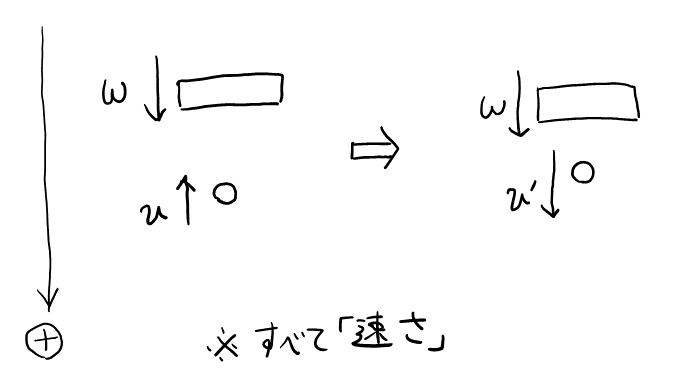
下向きを正とすると,
$$ 1 = -\frac{衝突後の速度の差}{衝突前の速度の差} = -\frac{w-v’}{w-(-v)} $$
より\( v’ \)を求める。
ヘト
再び衝突するまでに高さが変化しているので, へとトは独立に求めることは出来ず, 連立方程式が必要。図を書くと,
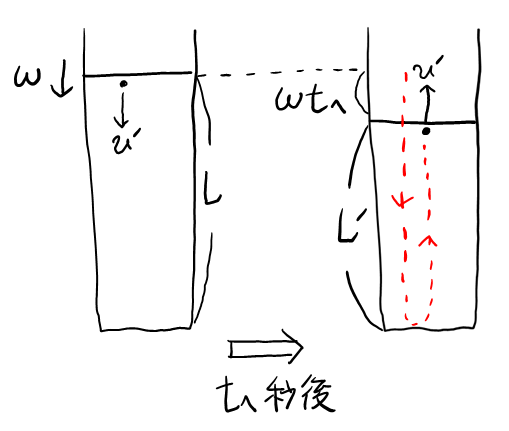
この図より, まず\( L = L’ + wt_ヘ \)が視覚的にわかる。また粒子は, 再衝突するまで速さ\( v’ \)で進むので, 「距離\( = \)速さ\( \times \)時間」より, \( \color{red}{L + L’} = v’ \times t_ヘ \)となる。これら2式より, \( t_ヘ \)と\( L’ \)を求める。
チ
計算するだけなので省略。問題文の近似で\( 1 \)となることも容易に確かめられる。
リヌ
問題文より, \( Lv = \)一定(\( = C \)とおく)。\( P = \frac{mv^2}{L} \)から\( v \)を消去すると, \( P = \frac{mC^2}{L^3} \)となる。
※ここで, \( mC^2 \)は定数なので, 新しく定数\( C \)で置き換えて, \( P = \frac{C}{L^3} \)と書く方がわかりやすい。
ル
変化前の圧力\( P = \frac{C}{L^3} \)と, 変化後の圧力\( P + \varDelta P = \frac{C}{(L – \Delta)^3} \)より, 圧力の増分\( \varDelta P \)を求める。問題文中に「釣り合って」という文言があるので, 変化前のつり合いの式\( P = Mg \)も忘れずに使う。
式中の\( \frac{1}{(L – \Delta)^3} \)の部分は, 与えられた近似式を使って, 例えば以下のように変形する。
\begin{eqnarray}
\frac{1}{(L – \Delta)^3} &=& (L – \Delta)^{-3} \\
&=& \left\{L\left(1 – \frac{\Delta}{L}\right)\right\}^{-3} \\
&=& L^{-3} \left(1 – \frac{\Delta}{L}\right)^{-3} \\
&=& \frac{1}{L^3} \left(1 + \frac{3\Delta}{L}\right)
\end{eqnarray}
なお, 与えられた近似は, \( x \)や\( a \)の符号が負の場合でも成り立つ, 一次近似の一番重要な式である。普遍的であるからこそ, 式変形の経路は様々考えられる。しかし, 一次近似を用いる以上, 経路にかかわらず, 最後の答えは必ず一致するということを覚えておいてほしい。
例えば今回の式変形で, 1度近似を行った結果, \( \frac{3Mg\Delta}{L – 3\Delta} \)という式が出てきてしまった場合も, 再び\( \frac{1}{L – 3\Delta} \)の部分に近似を適用すれば式変形が進められる。
ヲ
\( ma = -Kx (K > 0) \)の形で表されるとき, \( \omega = \sqrt{\frac{K}{m}} \)の単振動となる。
ここまでの流れより, 今回はおそらく\( K = \frac{3Mg}{L} \)の場合だろうと予想できる。念のため図を参考に, 座標をとって運動方程式を考えると, \( Ma = Mg – (P + \varDelta P) = -\frac{3Mg}{L}\Delta \)。
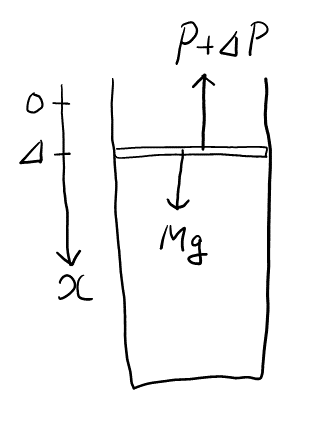
変位\( x \)は\( \Delta \)に対応するので, やはり\( K = \frac{3Mg}{L} \)の場合の単振動であることがわかり, \( \omega \)から周期を求めて終了。
振り返り
ヘトはただの算数の問題だが, 京大ではこのような問題はよく出題されている。物理の公式に頼らず, 図を書いて状況を把握する力が試される。
途中のリヌも多少難しいが, やはり最後のルヲがポイントになるだろう。単振動と近似という京大物理頻出の分野である。近似計算は, 式変形の経路によってかなりかかる時間が変わってくるので, いろんな式変形を自分で試して, 慣れておくことをおすすめする。
ルヲも含めて難易度的には無理のある問題ではない。しかし, 実際完答できる人はかなり少ないと思われるので, このレベルの問題を確実に取ることが大切である。
コメント