問題
次の文を読んで, に適した式をそれぞれの解答欄に記入せよ。
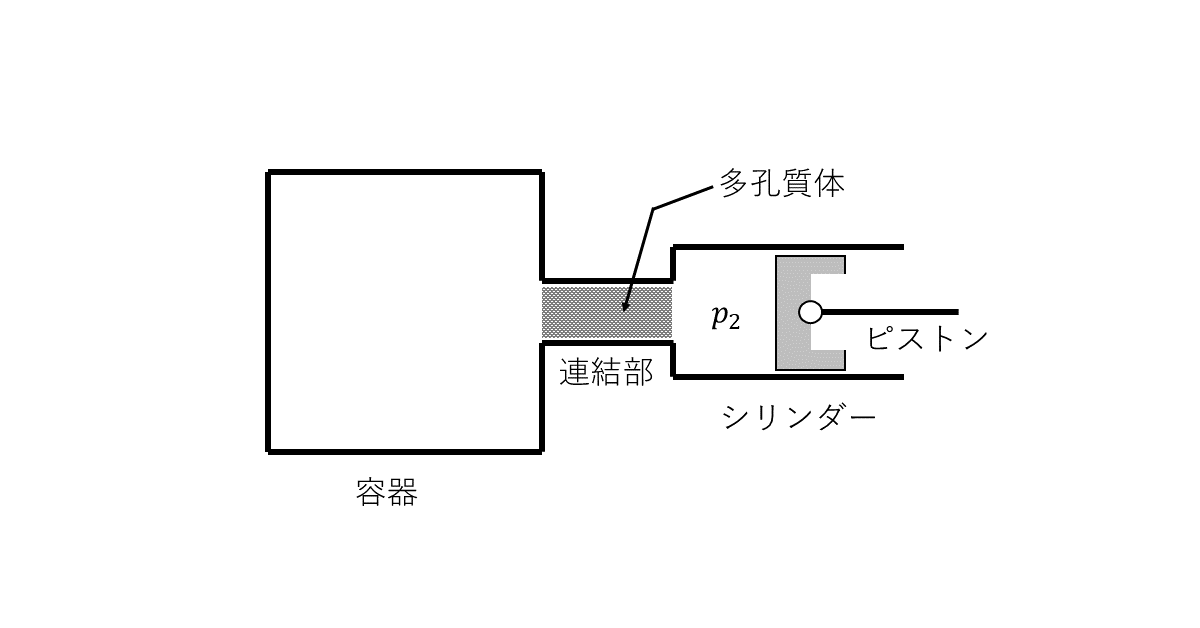
単原子分子の理想気体で満たされた容器とピストン付きシリンダーが連結された図1のような装置がある。ピストンは気密性がよく, 滑らかに動くことができるものとする。容器, 連結部, シリンダー, ピストンともに熱を伝えない材料でできている。また, 連結部にある気体の体積は, 容器やシリンダーの容積に比べて十分小さくゼロとみなせるものとする。気体定数を\( R \)として, この気体の定積モル比熱は\( \frac{3}{2}R \)で表せる。
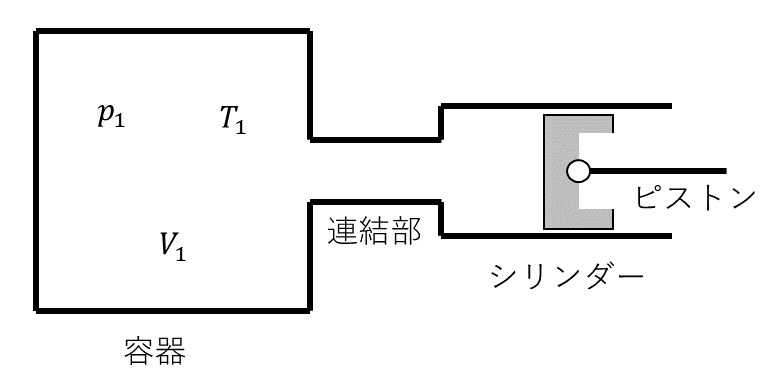
はじめ, 図1のように, 容積\( V_1 \)の容器内が圧力\( p_1 \), 温度\( T_1 \)の理想気体で満たされており, この状態を初期状態と呼ぶ。このとき, ピストンはシリンダーの左端にあってシリンダー内部にある気体の体積はゼロとみなせるものとする。
この場合について, 以下の過程Aおよび過程Bを考える。
過程A:
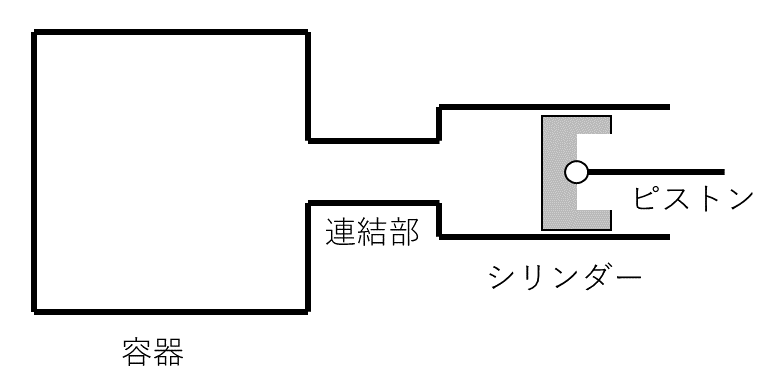
初期状態において容器内にあった気体が, 以下に示した(1)式の関係を保ちながら, 圧力\( p_1 \)から\( \alpha p_1 \)(ただし, \( 0 < \alpha < 1 \))まで断熱的に変化し, その気体の一部が図2に示すようにシリンダー内へ移動した。
\( pV^{\frac{5}{3}} = \)一定 ……(1)
ただし, \( p \)および\( V \)はそれぞれ, この仮定における気体の圧力および体積を表す。また, 気体の移動はゆるやかに起こり, その間, ピストンは常に, 容器内の気体の圧力と等しい圧力がかかっているものとする。
初期状態において容器内にあった気体のモル(\( \rm{mol} \))数は, アと書ける。気体の圧力が\( \alpha p_1 \)になったとき, 気体の温度はイ\( \times T_1 \)になる。この変化によって, 系全体の内部エネルギーの初期状態に対する増分はウ\( \times p_1V_1 \)になる。ゆえに, 移動した気体が外部になした仕事は, 熱力学の第1法則に従って, エと求めることができる。また, 気体の移動にともなって, シリンダー内の気体の体積はオ\( \times V_1 \)となり, シリンダー内へ移動した気体のモル数はカとなる。
過程B:
過程Bでは過程Aと異なり, 初期状態において, 細かい穴の多数あいた多孔質体と呼ばれるものが, 連結部に詰められている。この多孔質体は, シリンダー側の気体の圧力を常に一定に保つ役割を果たしている。この一定圧力の値を\( p_2 \)(ただし, \( 0 < p_2 < p_1 \))とする。
この場合について, 気体が外部に対してなす仕事や, 移動する気体のモル数を過程Aの場合と比較してみる。
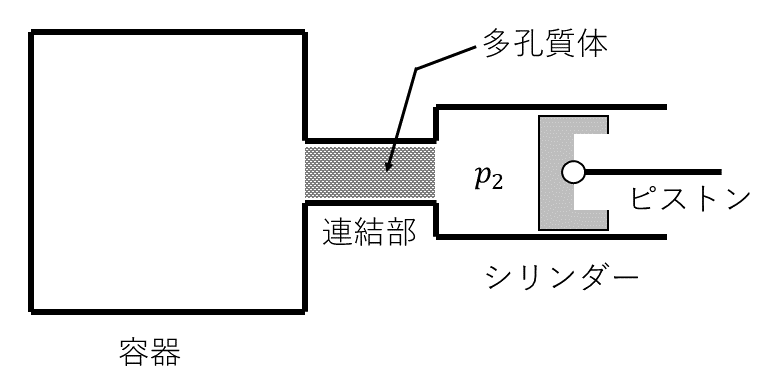
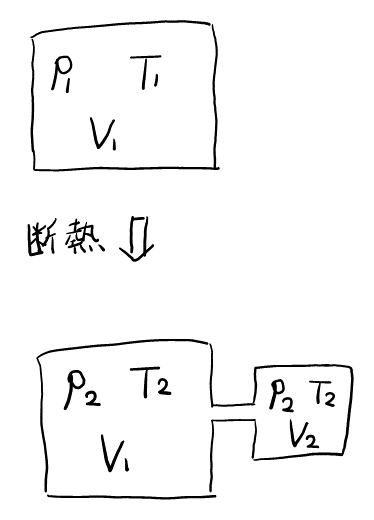
図3のように, はじめ容器内にあった気体の一部はシリンダー側に移動するが, 過程Bではその間, ピストンには常に, シリンダー内の気体の圧力\( p_2 \)と等しい圧力がかかっているものとする。十分に時間が経過すると, 容器内とシリンダー内の気体の温度は等しくなり, 容器内の気体の圧力も\( p_2 \)に等しくなった。このとき, シリンダー内の気体の体積を\( V_2 \)とすれば, 気体が外部に対してなした仕事は, キと書ける。過程Aの場合と同様に, 系全体の内部エネルギーの変化を考慮し, 熱力学の第1法則を適用すると, シリンダー内の気体の体積, 温度を求めることができる。いま, \( \beta = \frac{p_2}{p_1} \)とすると, この\( \beta \)を用いて, シリンダー内の気体の体積はク\( \times V_1 \), 気体の温度はケ\( \times T_1 \)と表すことができる。したがって, シリンダー内へ移動した気体のモル数はコとなる。
解説
単原子分子の理想気体であるから, 内部エネルギー\( U = \frac{3}{2}nRT \), 定積モル比熱\( C_V = \frac{3}{2}R \), 定圧モル比熱\( C_V = \frac{5}{2}R \)が使える。また, 内部エネルギーの変化\( \varDelta U = nC_V \varDelta T \)は, 単原子分子の理想気体に限らずいつでも使える。
過程A
ア
省略。
イ
断熱変化のポアソンの式「\( pV^{\frac{5}{3}} = \)一定」が与えられているので, これを用いる。
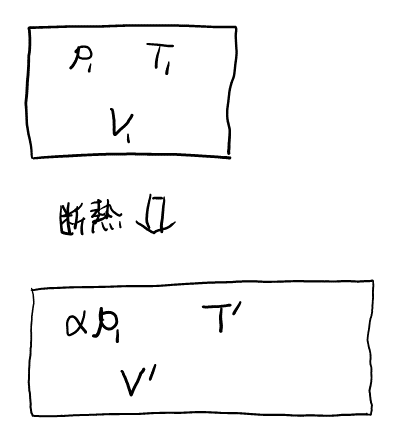
ポアソンの式\( pV^{\gamma} = \)一定より, まず\( V’ \)を求めてから, 状態方程式より\( T’ \)を求めることができる。
なお, ポアソンの式を\( T \)と\( V \)だけで表すために\( p = \frac{nRT}{V} \)を代入した「\( TV^{\gamma – 1} = \)一定」…①はよく使われる。一方で, \( p \)と\( T \)だけで表すために\( V = \frac{nRT}{p} \)を代入した「\( p^{1 – \gamma}T^{\gamma} = \)一定」…②はあまり見かけない。しかし, どちらも考え方は同じなので, 変形できるようにしておく必要はある。本問のように\( V \)を気にしたくなかったら, 与えられたポアソンの式から②を導いてから, それを使うと早い。
また, ポアソンの式では指数の式変形が多発する。基本的に以下の4つの公式(?)を使って, 多少時間がかかっても, 適度に分解しながら正しく式変形をすることに慣れておかないといけない。
・\( (xy)^a = x^a \times y^a \)
・\( x^{a+b} = x^a \times x^b \)
・\( (x^a)^b = x^{a \times b} \)
・\( x^{-a} = \frac{1}{x^a} \)
ウ
\( \varDelta U = nC_V \varDelta T \)を使うだけなので省略。
エ
熱力学第1法則は, 以下のように気体を主体として, inとoutを明示すると, 正負の間違いが無くなる。
\( Q_{\rm{in}} = \varDelta U + W_{\rm{out}} \)または\( \varDelta U = Q_{\rm{in}} + W_{\rm{in}} \)
今回は断熱変化なので当然\( Q_{\rm{in}} = 0 \)であり, 気体が外部にした仕事は, \( W_{\rm{out}} = -W_{\rm{in}} = -\varDelta U \)だからウとほぼ同じ。
オカ
イで\( V’ \)を出していない場合はここで必要となる。
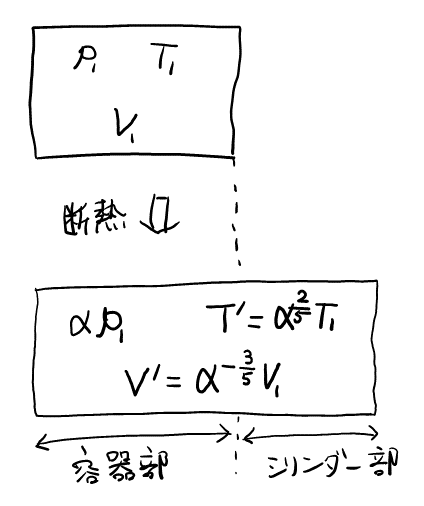
図より, シリンダー内の気体の体積は明らかに\( V’ – V_1 \)で求まる。また, 全\( n[\rm{mol}] \)が\( V_1 : V’ – V_1 \)で分配されるので, シリンダーのモルは\( n \times \frac{V’ – V_1}{V_1 + (V’ – V_1)} \)。
過程B
キ
状況がイメージしにくいかもしれない。いろいろ書いてあるが, ピストンにかかる圧力は常に\( p_2 \)である。よって, \( p \)一定の時の仕事の大きさ\( |W| = |p \varDelta V| \)が使える。今回, 気体は膨らんでいるので, 外部に仕事をしている(つまり, 答えは正)。
クケ
シリンダーの体積\( V_2 \), 温度\( T_2 \)の2変数なので, 式を2つ立てる。
1つ目は, 問題文に書いてある通り, 熱力学第1法則。過程Aと同様に, \( W_{\rm{out}} = -\varDelta U \)より, \( p_2V_2 = -nC_V(T_2 – T_1) \)。
(\( W_{\rm{out}} = p_2V_2 \)はキの答えより)
2つ目は特に誘導は無いが, \( V_2 \)と\( T_2 \)を含む状態方程式が変化後の図より立てられて, \( p_2 (V_1 + V_2) = nRT_2 \)。
以上2つの式を解けばよい。
コ
おまけの問題で, 過程Aの最後と同じ。
振り返り
頻出の断熱変化の問題で, 京大受験生ならば何度も類題を演習していないといけない内容。特に目立った難問は無く(クケの計算が多少ややこしい程度), 標準的な難易度と言えるが, 本番でミスせず最後まで完答するのはかなり難しいと思われる。普段の演習から, まずはこのレベルの問題を, 時間内に解ききれるようにする練習が大切である。
コメント